Zmniejszenie funkcji, jak ją zidentyfikować, przykłady, ćwiczenia

A zmniejszenie funkcji f jest tym, którego wartość maleje wraz ze wzrostem wartości x. Oznacza, że ​​w danym przedziale, biorąc pod uwagę dwie wartości x₁ i x₂ Takie, że x₁ < x₂, Następnie F (x₁)> f (x₂).

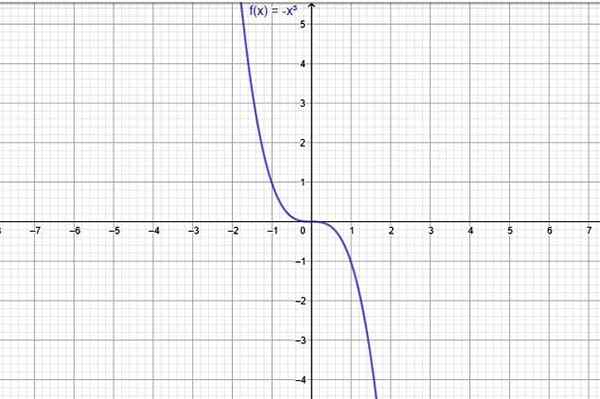
Przykładem funkcji, która zawsze maleje, jest f (x) = -x³, którego wykres pokazuje na poniższym rysunku:

Rysunek 1. Funkcją, która zawsze maleje w całej swojej domenie, jest f (x) = -x^3. Źródło: f. Zapata przez Geogebra.

Chociaż niektóre takie funkcje charakteryzują się zmniejszeniem w całej ich domenie, nie wszystkie zachowują się w ten sposób, rośnie, a także te, które rosną i zmniejszają w niektórych odstępach domeny. Badanie interwałów wzrostu i zmniejszenia nazywane jest monotonia funkcji.

Podobnie wzrost lub spadek funkcji można rozważyć w określonym punkcie domeny. Ale każda funkcja, która maleje w danym przedziale, jest również w każdym punkcie, który do niej należy.

[TOC]

Jak zidentyfikować funkcję malejącą?

Wykres funkcji wskazuje wizualnie, czy maleje, czy nie. Jeśli podczas poruszania się w rosnącym sensie X, funkcja „zejścia”, oznacza to, że maleje.

A jeśli masz przedziały, w których zmniejsza się i rośnie na przemian, co jest najbardziej zwykle, ponieważ są one wyraźnie ujawnione poprzez obserwowanie zachowania funkcji w całej jej domenie, ponieważ będą interwgliny, w których funkcja „wznosi się” i inne w środku, a inne w które „zejście”.

Alternatywnie, jeśli wykres funkcji nie jest dostępny, analitycznie możliwe jest ustalenie, czy maleje w jednym punkcie lub w okresie, poprzez pierwszą pochodną.

Kryterium pierwszej pochodnej

Zwróć uwagę na zachowanie funkcji malejącej pokazanej na rycinie 2. Segmenty różowej linii są styczne do punktów, których współrzędne są [a, f (a)] I [A+H, F (A+H)] i mają negatywne nachylenie.

Może ci służyć: w jaki sposób informacje są uzyskane w ankiecie?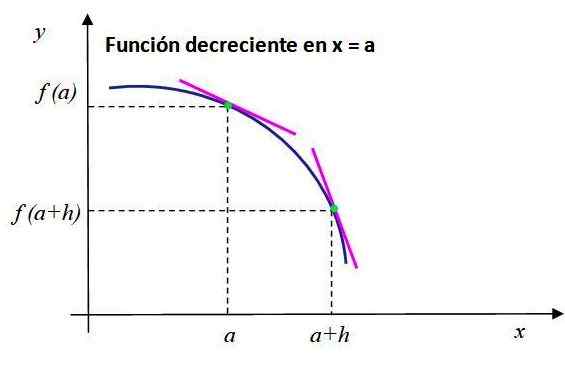Rysunek 2. Nachylenie linii stycznej do wykresu F (x) jest ujemne przy x = a, wówczas funkcja maleje w tym momencie. Źródło: f. Zapata.

W przypadku tej funkcji następujące są spełnione:

F (a+h) - f (a) < 0 ⇒  F (A+H) < f (a)

Dlatego można uznać, że funkcja maleje x = a.

Jednak pierwsze pochodzące z funkcji f (x), oceniane przy x = a, które z definicji jest nachyleniem linii stycznej do krzywej przy x = a, jest podana przez:

Limit wskazuje, że wartość H można wykonać tak małą, jak chcesz i sugeruje, że znak fa), Można go użyć, aby wiedzieć, czy funkcja maleje w określonym punkcie, o ile w tym momencie istnieje pochodna.

W takim razie tak fa) < 0, Można potwierdzić, że funkcja maleje i przeciwnie, jeśli f '(a)> 0, Wtedy funkcja rośnie w tym momencie.

Twierdzenie o zmniejszeniu i rozwijaniu funkcji

Wcześniej odniesiono się do zachowania funkcji w danym momencie. Teraz następujące twierdzenie pozwala poznać interwały, w których funkcja maleje, rośnie lub stała:

Niech F będzie funkcją różniczkową w przedziale (a, b). To prawda, że:

-Tak F '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Jeśli wręcz przeciwnie f '(x)> 0 dla wszystkich x należących do (a, b), mówi się, że funkcja f (x) rośnie w (a, b).

-Wreszcie, jeśli f '(x) = 0 dla wszystkich x, który należy do interwału (a, b), f (x) jest stały we wspomnianym przedziale.

Demonstracja

Załóżmy, że F '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ i x₂ należący do wspomnianego przedziału i warunku, że x₁< x₂.

Twierdzenie o średniej wartości stwierdza, że ​​istnieje liczba rzeczywista C, między x₁ i x₂, tak, że:

Może ci służyć: wspólny czynnik grupowania warunków: przykłady, ćwiczenia

Zgodnie z ustalonym od x₁< x₂,  Δx jest dodatni. Tak więc, ponieważ f '(c) jest ujemne, więc δy jest również. Dlatego f (x₁) jest większy niż f (x₂) A funkcja skutecznie maleje we wszystkich punktach w przedziale (a, b).

Kroki, aby wiedzieć, czy funkcja maleje

Aby znaleźć interwały spadku i wzrostu funkcji poprzez zastosowanie poprzedniego twierdzenia, kroki te są przestrzegane:

-Znajdź pierwszy pochodzący z funkcji i dopasuj ją do zera, rozwiązując wynikowe równanie. Określ także punkty, w których pochodna nie istnieje.

Wszystkie te punkty są nazywane punkt krytyczny I trzeba je znaleźć, ponieważ w nich pochodna ma możliwość zmiany znaku, co wskazuje, że funkcja przechodzi od wzrostu do zmniejszenia lub przeciwnych.

-Domena funkcji jest podzielona na przedziały określone przez punkty, w których pierwsza pochodna jest anulowana lub nie istnieje.

-Wreszcie znak pochodnej jest badany w dowolnym punkcie, który należy do każdego z przedziałów uzyskanych w poprzednim kroku.

Przykłady zmniejszania funkcji

Funkcje nie zmniejszają się w tej samej tempie, niektóre robią to szybciej niż inne. Następujące funkcje, które pojawiają się często w praktyce, zmniejszają się:

Funkcja wykładnicza

Funkcja formularza F (x) = a^X, Z od 0 do 1, nie włączając ich, szybko zmniejsza się w całej domenie.

Funkcja 1/x

Poprzez internetowy program graficzny jako geogebra, wykres funkcji f (x) = 1/x, potwierdzając, że maleje on w całej swojej domenie.

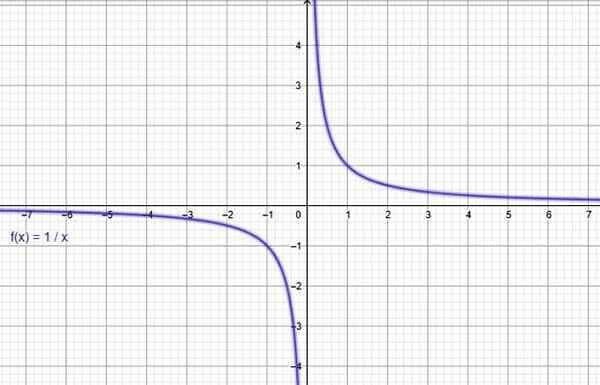Rysunek 3. Funkcja f (x) = 1/x maleje. Źródło: f. Zapata przez Geogebra.

Powiązana funkcja

Funkcje formy y = mx + b z m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Może ci służyć: równość matematyczna

Ćwiczenie rozwiązane

Znajdź, jeśli w ogóle, przedziały zmniejszania funkcji:

f (x) = x⁴ - 6x² - 4

Rozwiązanie

Pierwszym krokiem jest znalezienie f '(x):

f '(x) = 4x³ - 12x

Pierwsza pochodna F (x) jest funkcją ciągłą, to znaczy nie ma punktów nieciągłości, ale jest anulowana w:

4x³ - 12x = 0 = 4x (x²-3) = 0

Rozwiązania tego równania to: x₁ = 0, x₂ = - √3 i x₃ = √3. Są to punkty krytyczne, które dzielą domenę f (x) w przedziałach: (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Wówczas oceniana jest pierwsza wyprowadzona w dowolnej wartości x, która należy do każdego przedziału. Wartości te zostały wybrane:

Dla (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

Dla (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

Dla (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

Dla (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Podobnie jak kilka interwałów, dobrym pomysłem jest stworzenie tabeli, aby zorganizować wyniki. Strzałka w górę wskazuje, że funkcja rośnie i w dół, co zmniejsza się:

Stwierdzono, że funkcja maleje w odstępach (-∞,- √3) i (0, √3) i rośnie w pozostałych odstępach czasu. Oryginalna funkcja w Geogebra jest łatwo sprawdzana przez wykres.

Bibliografia

1. Ayres, f. 2000. Obliczenie. 5Ed. MC Graw Hill.
2. Leithold, L. 1992. Obliczanie za pomocą geometrii analitycznej. Harla, s.DO.
3. Purcell, e. J., Varberg, d., & Rigdon, s. I. (2007). Obliczenie. Meksyk: Pearson Education.
4. Matemobile. Funkcje, rosnące, malejące i stałe. Odzyskany z: Matemovil.com
5. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.