Ogólne równania kwadratowe, przykłady, ćwiczenia

Ogólna formuła, który jest również znany jako Formuła rozpuszczalnika W niektórych tekstach służy do rozwiązania równań drugiego stopnia: topór² + BX + C = 0.

W nich Do, B I C Są to liczby rzeczywiste, z tym warunkiem Do różni się od 0, by X Nieznane. Następnie ogólna formuła przedstawia klirens nieznanego przez wyrażenie, które obejmuje wartości Do, B I C następująco:

Rysunek 1. Ogólna formuła matematyki służy do rozwiązania równań kwadratowych. Źródło: f. Zapata.

I dzięki tej wzorze można znaleźć rozwiązanie dowolnego równania drugiego stopnia lub kwadratowego, pod warunkiem, że istnieje roztwór.

Według historyków ogólna formuła była już znana przez starożytną matematykę babilońską. Następnie został przekazany na inne narody, takie jak Egipcjanie i Grecy, poprzez wymiany kulturowe.

Formuła i jej warianty przybyły do ​​Europy dzięki muzułmańskim matematykom osiedlili się na Półwyspie Iberyjskim. Nie używali jednak notacji algebraicznej, której obecnie używamy. Ta notacja jest spowodowana francuskim matematykiem i XX wieku ekspertem kryptograficznym Francois Viete.

[TOC]

Równania kwadratowe według ogólnego wzoru

Zobaczmy, jak powstaje ogólna formuła, aby zweryfikować jej ważność. Zaczynając od ogólnego równania kwadratowego:

topór² + BX + C = 0

Zajmijmy się prostymi manipulacjami algebraicznymi, aby osiągnąć prześwig nieznanego. Istnieje kilka sposobów noszenia tego, na przykład wypełniania kwadratów, jak pokazano wtedy.

Demonstracja ogólnej formuły

Zaczynamy od dodania (-C) po obu stronach równości:

topór² + Bx = - C

A teraz jest mnożony przez 4a, zawsze po obu stronach równości, aby nie zmieniać wyrażenia:

4² X² + 4ab x = - 4ac

Dodanie b²:

4²⋅x² + 4AB⋅x + b² = - 4ac + b²

Celem tego jest wypełnienie kwadratów po lewej stronie równości, która zawiera nieznane, w ten sposób jego zezwolenie jest ułatwione. Zatem:

Może ci służyć: dzielnicy 8: co to jest i łatwe wyjaśnienie

-Pierwszy termin: 4² X² Jest to idealny kwadrat 2AX

-Ostatni, czyli b², To idealny kwadrat B.

-A centralnym terminem jest podwójny produkt 2AX i B: 2⋅2AX=B = 4ABX

Dlatego mamy kwadratowy dwumian:

4²⋅x² + 4AB⋅x + b² = (2AX + B)²

I możemy napisać:

(2AX + B)² = - 4ac + b²

Jesteśmy o krok od oczyszczenia nieznanego X:

I już otrzymujemy ogólną formułę, którą znamy:

Istnieją inne sposoby na algebraiczne manipulowanie równaniem kwadratowym i uzyskanie tego samego wyniku.

Przykłady użycia ogólnej formuły

Aby zastosować ogólną formułę, wartości A, B i C są starannie określane i zastępowane w wzorze. Zwróć uwagę na symbol mniej więcej w licznikach; Wskazuje to, że musimy rozważyć dwie możliwości dotyczące operacji, jedna z znakiem + i jedną z znakiem -.

Równanie kwadratowe może mieć następujące rozwiązania, zgodnie z wartością ilości sub-radycznej, znanej jako dyskryminacyjny:

-Tak b² - 4AC> 0, równanie kwadratowe ma dwa rzeczywiste i różne rozwiązania.

-Kiedy b² - 4ac = 0, równanie ma unikalne rozwiązanie, podane przez:

x = -b/2a

-Wreszcie, jeśli b² - 4ac < 0, la ecuación no tiene soluciones reales, pero sí tiene soluciones complejas.

Spójrzmy na niektóre przykłady, w których stosuje się ogólną formułę, zauważając, że jeśli którykolwiek ze współczynników, które towarzyszą nieznanym, nie pojawi się, rozumie się, że warto 1 1. A jeśli niezależny termin jest ten, którego nie znaleziono, jest wart 0.

- Przykład 1

Rozwiąż następujące równania kwadratowe:

a) 6x² + 11x -10 = 0

b) 3x² -5x -1 = 0

Odpowiedz

Piszemy współczynniki każdego terminu: a = 6, b = 11, c = -10 i zastępują wartości w formule ogólnym:

Może ci służyć: opodatkowanie

x = (-11 ± 19) /12

Wynik prowadzi do następujących dwóch rzeczywistych rozwiązań:

X₁ = (-11 + 19)/12 = 8/12 = 2/3

X₂ = (-11-19)/12 = -5/2

Odpowiedź b

Ponownie określa się współczynniki: a = 3, b = -5 i c = -1. Zastępując w formule:

W przeciwieństwie do poprzedniego przypadku, pierwiastek kwadratowy 37 nie jest liczbą całkowitą, ale możemy również podnieść dwa rozwiązania i pozostawić korzeń lub znaleźć odpowiednią wartość dziesiętną za pomocą kalkulatora:

X₁ = (-5 + √37)/6 ≈ 0.18

X₂ = (-5 - √37)/6 ≈ - 1.85

- Przykład 2

Rozwiąż równanie drugiego stopnia x² - 4x +13 = 0.

Odpowiedź

Jak zawsze identyfikujemy wartości współczynników i zastępujemy ogólny wzór: a = 1, b = - 4, c = 13. To prowadzi do:

Mamy korzeń ujemny, dlatego roztwory tego równania są liczbami złożonymi. Korzeń można wyrazić w kategoriach Siema, Wyimaginowa jednostka:

√ (36i²) = 6i

Odkąd ja² = -1 Dlatego złożone rozwiązania to:

X₁ = (4 + 6i)/2 = 2 + 3i

X₂ = (4 - 6i)/2 = 2 - 3i

Ćwiczenie rozwiązane

Długie schody 10 m spoczywa na pionowej ścianie, z stopą 6 m od tej ściany. Schody poślizgają się, a stopa jest oddzielona o 3 m więcej od podstawy.

Znajdź pionową odległość, która biegnie przez górną część schodów.

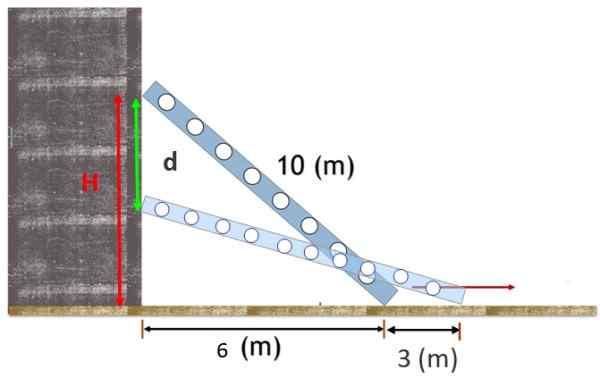Rysunek 2. Schody podtrzymywane na ścianie trochę poślizgają się, a górny przystanek porusza się pionowo. Źródło: f. Zapata.

Rozwiązanie

Aby znaleźć pionową odległość, która przesuwa górną część schodów, musisz znaleźć pozycję, w której pierwotnie dotyczyła ziemi. Możemy to zrobić z twierdzeniem Pitagorasa, ponieważ utworzona liczba jest postacią prawego trójkąta:

H = (10² - 6²) ^½ = 8 m

Po poślizgnięciu się schodów porusza się odległość D, Zmierz, ponieważ góra miała 8 m wysokości, aż do osiągnięcia nowej pozycji, na metrach (H-D) nad ziemią. Nieznane do wyczytania to d.

Może ci służyć: nagromadzona częstotliwość: wzór, obliczenia, rozkład, przykłady

Aby go znaleźć, proponujemy nowy trójkąt prostokąta, który powstaje po tym, jak drabina trochę poślizgnęła. Ten trójkąt nadal ma hipotenusę równą 10 mi, a równolegle Cateto wynosi teraz 6m + 3m = 9 m, dlatego:

(H-D)² = 10² - 9² = 100 - 81 = 19

Wcześniej obliczamy H = 8m, wcześniej obliczono:

(8-D)² = 19

Równanie można rozwiązać na kilka sposobów, w tym zastosowanie ogólnej formuły, które pokażemy poniżej z tymi krokami:

Krok 1

Opracuj godną uwagi lewą po lewej:

64 -16d + d² = 19

Krok 2

Ustalić równanie drugiego stopnia dla nieznanego D:

D² - 16d + 45 = 0

Krok 3

-Współczynniki to: a = 1, b = -16 i c = 45, zastępujemy je w ogólnym wzorze:

Rozwiązania równania to:

D₁ = (16 + √76)/2 ≈ 12.36 m

D₂ = (16 - √76)/2 ≈ 3.64 m

Krok 4

Uzyskane rozwiązania są analizowane: pierwszy nie ma sensu fizycznego, ponieważ drabina nie jest możliwa do skompilowania 12.36 m, jeśli pierwotnie przystanek miał 8 m wysokości na ziemi.

Dlatego poprawna odpowiedź jest drugim rozwiązaniem: górna część schodów przesuwa d = 3.64 m.

Czy czytelnik może rozwiązać problem, stosując inną metodę?

Bibliografia

1. Baldor. 1977. Algebra podstawowa. Wenezuelskie wydania kulturalne.
2. Hoffman, J. Wybór problemów z matematyką. Głośność 2.
3. Jiménez, r. 2008. Algebra. Prentice Hall.
4. Stewart, J. 2006. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.