Dynamiczne lub kinetyczne współczynnik tarcia, przykłady, ćwiczenia

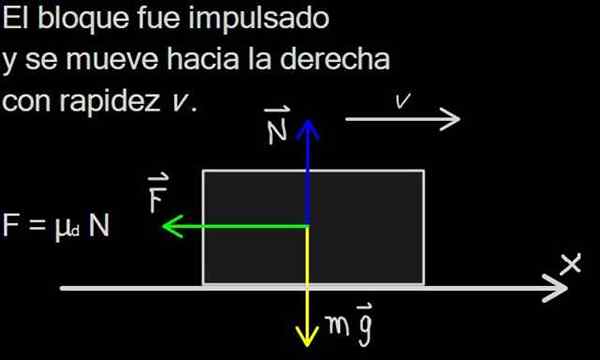
Dynamiczne tarcie lub kinetyczne Jest to ta, która występuje między dwoma ciałami w kontakcie, gdy powierzchnia jednego z nich porusza się w odniesieniu do powierzchni drugiej. Na przykład w pudełku, które przesuwa tarcie na nachyleniu, jest dynamiczna i rozłożona na powierzchni styku bloku.

Nachylenie musi być wystarczająco duże, aby styczny składnik ciężaru jest równy lub pokonał siłę tarcia, w przeciwnym razie blok, który zejdą.

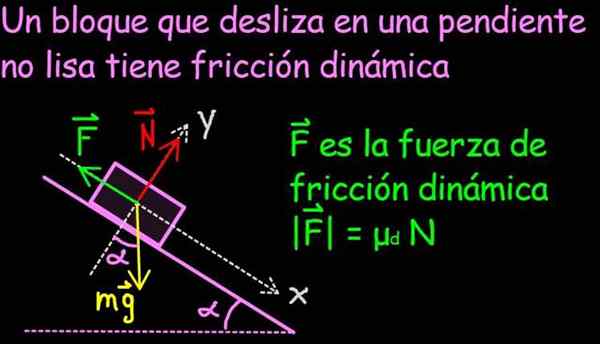Rysunek 1. Siła tarcia jest rozmieszczona na powierzchni styku bloku, ale na schemacie sił jest reprezentowana jako pojedyncza siła f, źródło: f. Zapata

Siła tarcia ma ogromne znaczenie w życiu codziennym, ponieważ pozwala na lokomocję ludzi, zwierząt i pojazdów. Na powierzchni bez tarcia, takiej jak lody, nie można rozpocząć ruchu.

Tarcie pozwala również naszym samochodom zatrzymać się po przeprowadzce.

Podczas nakładania hamulców podkładki hamulcowe są dokręcane na tarcze kół i dzięki dynamicznemu tarciu zatrzymaj ich obrót. Ale nie wystarczy mieć dobre hamulce, konieczne jest, aby istniała wystarczająca siła tarcia między oponami a podłogą, ponieważ w końcu jest to siła, na której polegamy, aby samochód się zatrzymał.

Ludzkość nauczyła się radzić sobie z tarciem dla swojej korzyści. Tak zaczął się od zastosowania tarcia między dwoma kawałkami suchego drewna, aby rozpalić ogień.

Natura nauczyła się również radzić sobie z tarciem na swoją korzyść. Na przykład błony maziowe pokrywające kości stawów są jedną z powierzchni o najniższym współczynniku tarcia.

[TOC]

Dynamiczny współczynnik tarcia

Pierwszym, który systematycznie badał ruch bloku, który przesuwa się na płaskiej powierzchni, był Leonardo da Vinci, ale jego badania nie zostały niezauważone.

Może ci służyć: Model atomowy Dirac Jordan: Charakterystyka i postulaty

Dopiero w XVII wieku francuski fizyk Guillaume Amontons na nowo odkrył prawa tarcia:

Dynamiczne przepisy dotyczące tarcia

1.- Siła tarcia obecna w bloku, która przesuwa się po płaskiej powierzchni, zawsze sprzeciwia się kierunku ruchu.

2.- Wielkość dynamicznej siły tarcia jest proporcjonalna do normalnej szczelności lub siły między powierzchniami bloku a płaszczyzną wsporową.

3.- Stała proporcjonalna jest współczynnikiem tarcia, statyczny μ_I W przypadku braku poślizgu i dynamicznego μ_D Kiedy jest. Współczynnik tarcia zależy od materiałów w kontakcie i stanu chropowatości.

4.- Siła tarcia jest niezależna od pozornego obszaru kontaktowego.

5.- Gdy ruch jednej powierzchni zaczyna się w odniesieniu do drugiej, siła tarcia jest stała i nie zależy od względnej prędkości między powierzchniami.

W przypadku nie ma ślizgania się, stosuje się tarcie statyczne, którego siła jest mniejsza lub równa współczynnikowi tarcia statycznego pomnożonego przez normy.

Rysunek 2. Dynamiczna siła tarcia sprzeciwia się kierunku ruchu, a jego wielkość jest proporcjonalna do siły normalnej. Stała proporcjonalności jest dynamicznym współczynnikiem tarcia. Źródło: f. Zapata.

Ostatnia własność była wynikiem wkładu francuskiego fizyka Charlesa Augustina z Coulomba, lepiej znanego ze swojego słynnego prawa siły między określonymi zarzutami elektrycznymi.

Te obserwacje prowadzą nas do modelu matematycznego dla dynamicznej siły tarcia F:

F = μ_D N

Gdzie μ_D Jest to dynamiczny współczynnik tarcia i N jest normalną siłą.

Jak określić dynamiczny współczynnik tarcia?

Dynamiczny współczynnik tarcia między dwiema powierzchniami jest określany eksperymentalnie. Jego wartość zależy nie tylko od materiałów na obu powierzchniach, ale od stanu chropowatości lub polerowania, a także od czystości.

Może ci służyć: fale mechaniczne: cechy, właściwości, wzory, typy

Jednym ze sposobów określenia tego jest zwiększenie i przesuwanie znanego pudełka na poziomej powierzchni.

Jeśli prędkość jest znana w momencie prowadzenia, a odległość przebywająca od tego czasu jest mierzona, możliwe jest znanie przyspieszenia hamowania z powodu dynamicznego tarcia.

Eksperyment 

W tym eksperymencie mierzona jest początkowa prędkość v i odległość D, Więc przyspieszenie hamowania to:

A = - v² / 2d

Schemat sił pokazano na rycinie 2. Wielkość masy jest masą m bloku pomnożonego przez przyspieszenie grawitacji g, i jak wiadomo, waga zawsze wskazuje pionowo w dół.

N Jest to normalna siła z powodu pchnięcia powierzchni nośnej i zawsze jest prostopadła (lub normalna) do płaszczyzny. Normalne istnieje, gdy powierzchnie są w kontakcie i ustaje, gdy tylko powierzchnie zostaną oddzielone.

Siła F reprezentuje dynamiczną siłę tarcia. Jest faktycznie rozmieszczony na dolnej powierzchni bloku, ale możemy reprezentować go jako pojedynczą siłę F zastosowane na środku bloku.

Ponieważ istnieje równowaga pionowa, wielkość normalnej N Jest równy wagi Mg:

N = mg

W kierunku poziomym siła tarcia powoduje spowolnienie masowego bloku M zgodnie z drugim prawem Newtona:

-F = m a

Siła tarcia F wskazuje w lewo, więc jego poziomy składnik jest ujemny, M jest masą bloku, a A jest przyspieszeniem hamowania.

Wcześniej uzyskano A = - v² / 2d A także model dynamicznego tarcia wskazuje::

F = μD n

Zastąpienie w poprzednim równaniu masz:

-μ_D N = - v² / 2d

Biorąc pod uwagę, że n = mg, możesz już wyczyścić dynamiczny współczynnik tarcia: 

Może ci służyć: model atomowy Schrödingera

μ_D = v² / (2d mg)

Tabela współczynnika Rocy niektórych materiałów

Poniższa tabela pokazuje statyczne i dynamiczne współczynniki tarcia dla różnych materiałów. Należy zauważyć, że systematycznie współczynnik tarcia statycznego jest zawsze większy niż dynamiczny współczynnik tarcia.

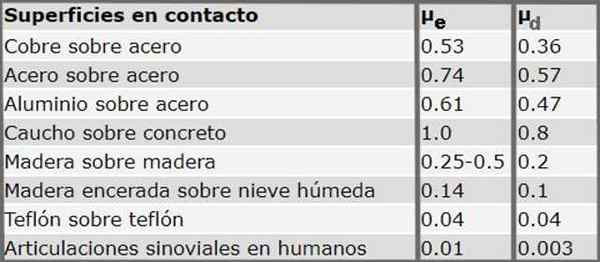Rysunek 3. Statyczne i dynamiczne współczynniki tarcia dla kilku powierzchni w kontakcie. Źródło: Serway R.DO. Fizyczny. McGraw-Hill (1992)

Ćwiczenia

- Ćwiczenie 1

Promowany jest blok ciasta na 2 kg na podłodze poziomej i jest zwolniony. W momencie zwolnienia rejestrowana jest prędkość 1,5 m/s. Od tego momentu, aż blok zatrzyma się według dynamicznego tarcia 3 m. Określ współczynnik tarcia kinetycznego.

Rozwiązanie

Zgodnie z wzorem uzyskanym w przykładzie poprzedniej sekcji jest to współczynnik dynamiczny (lub kinetyczny):

μ_D = v² / (2d mg) = 1.52 / (2x3x2 x9,8) = 0,019.

- Ćwiczenie 2

Wiedząc, że blok na rycinie 1 opada ze stałą prędkością, że masa bloku wynosi 1 kg i że nachylenie płaszczyzny wynosi 30º, określa:

a) wartość dynamicznego tarcia

b) dynamiczny współczynnik tarcia między blokiem a płaszczyzną.

Rozwiązanie

Na rycinie 4 równanie ruchu (drugie prawo Newtona) pokazano dla problemu bloku, który schodzi na zbocze ze współczynnikiem tarcia μ_D  i nachylenie α (patrz schemat sił na rycinie 1)

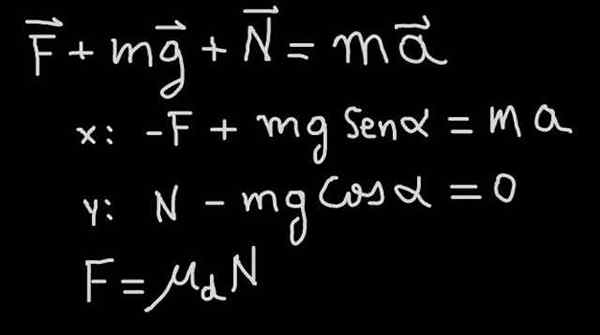Rysunek 4. Drugie prawo Newtona dotyczyło bloku, który przesuwa się na zboczu z tarciem. Źródło: f. Zapata.

W naszym ćwiczeniu powiedziano nam, że blok schodzi ze stałą prędkością, dlatego opada z przyspieszeniem a = 0. Stamtąd wynika z tego, że siła tarcia jest taka, że ​​równa się ona składnik styczny masy: f = mg sen (α).

W naszym przypadku m = 1 kg i α = 30º, więc siła tarcia f ma wartość 4,9N.

Z drugiej strony siła normalna n jest taka sama i sprzeczna z prostopadłym składnikiem masy: n = mg cos (α) = 8,48 n .

Stamtąd wynika z tego, że dynamiczny współczynnik tarcia to:

μ_D = F / n = 4,9N / 8,48N = 0,57

Bibliografia

1. Alonso m., Finn e. 1970. Fizyczny. Tom I. Mechanika. Międzyamerykańskie fundusz edukacyjny.DO.
2. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
3. Hewitt, str. 2012. Konceptualna nauka fizyczna. PIĄTA EDYCJA.
4. Rex, a. 2011. Podstawy fizyki. osoba. 
5. Serway r. 1992. Fizyczny. McGraw-Hill.
6. Young, h. 2015. Fizyka uniwersytecka z nowoczesną fizyką. 14. edycja. osoba.