Nagromadzony wzór częstotliwości, obliczenia, rozkład, przykłady

zgromadzona częstotliwość Jest sumą bezwzględnych częstotliwości f, od dziecka, do którego odpowiada określonej wartości zmiennej. Z kolei częstotliwość bezwzględna to liczba razy, kiedy obserwacja pojawia się w zestawie danych.

Oczywiście zmienna badań musi być uporządkowana. A ponieważ nagromadzona częstotliwość jest uzyskiwana przez dodanie bezwzględnych częstotliwości, okazuje się, że skumulowana częstotliwość do ostatnich danych musi pokryć się z całkowitą liczbą. W przeciwnym razie występuje błąd w obliczeniach.

Skumulowana częstotliwość jest wykorzystywana w zarządzaniu danymi statystycznymi

Ogólnie rzecz biorąc, skumulowana częstotliwość jest oznaczona jako F_Siema (Lub czasami n_Siema), aby odróżnić go od absolutnej częstotliwości F_Siema i ważne jest, aby dodać do niej kolumnę w tabeli, z którą dane są zorganizowane, zwane Tabela częstotliwości.

W ten sposób ułatwia się między innymi, aby zachować opis liczby danych, aż do pewnej obserwacji.

A f_Siema Jest również znany jako Absolutna skumulowana częstotliwość. Jeśli podzielisz się na całkowitą dane, masz Względna skumulowana częstotliwość, którego ostateczna suma musi być równa 1.

[TOC]

Formuły

Skumulowana częstotliwość określonej wartości zmiennej x_Siema  Jest to suma częstotliwości bezwzględnych F wszystkich wartości niższych lub równych:

F_Siema  = f₁ + F₂ + F₃  +… F_Siema

Dodając wszystkie bezwzględne częstotliwości, otrzymuje się całkowitą liczbę danych N, to znaczy:

F₁ + F₂ + F₃ +.. . + F_N = N

Poprzednia operacja jest zapisana w sposób podsumowujący przez symbol suma ∑:

∑ f_Siema = N

Inne nagromadzone częstotliwości

Można również zgromadzić następujące częstotliwości:

-Częstotliwość względna: Uzyskuje się go przez podzielenie częstotliwości bezwzględnej F_Siema Między danymi całkowitych n:

F_R = f_Siema / N

Jeśli częstotliwości względne są dodawane od dziecka do tego odpowiadającego określonej obserwacji, nagromadzona częstotliwość względna. Ostatnia wartość musi być równa 1.

-Skumulowany skumulowany procent częstotliwości: Zgromadzona częstotliwość względna na 100% jest mnożona.

F_% = (f_Siema / N) x 100%

Częstotliwości te są przydatne do opisania zachowania danych, na przykład poprzez znalezienie centralnych miar tendencji.

Jak uzyskać nagromadzoną częstotliwość?

Aby uzyskać skumulowaną częstotliwość, konieczne jest zamówienie danych i uporządkowanie ich w tabeli częstotliwości. Procedura jest zilustrowana w następującej praktycznej sytuacji:

Może ci służyć: sukcesja złożona

-W sklepie internetowym, który sprzedaje telefony komórkowe, rekord sprzedaży określonej marki marca, następujące wartości dziennie:

1; 2; 1; 3; 0; 1; 0; 2; 4; 2; 1; 0; 3; 3; 0; 1; 2; 4; 1; 2; 3; 2; 3; 1; 2; 4; 2; 1; 5; 5; 3

Zmienna to Liczba telefonów sprzedawanych dziennie I jest ilościowy. Przedstawione dane nie są tak łatwe do interpretacji, na przykład właściciele sklepu mogą być zainteresowani wiedzą, czy istnieje jakikolwiek trend, na przykład dni tygodnia, kiedy sprzedaż tej marki jest większa.

Informacje takie i więcej, można je uzyskać, prezentując dane w uporządkowany sposób i określając częstotliwości.

Jak wypełnić tabelę częstotliwości

Aby obliczyć zgromadzoną częstotliwość, dane są uporządkowane:

 0; 0; 0; 0; 1; 1; 1; 1; 1; 1; 1; 1; 2; 2; 2; 2; 2; 2; 2; 2; 3; 3; 3; 3; 3; 3; 4; 4; 4; 5; 5

Następnie zbudowano tabelę z następującymi informacjami:

-Pierwsza kolumna po lewej z ilością sprzedanych telefonów, od 0 do 5 i w rosnącej kolejności.

-Druga kolumna: Częstotliwość bezwzględna, która jest liczbą dni, które zostały sprzedane 0 telefonów, 1 telefon, 2 telefony i tak dalej.

-Trzecia kolumna: skumulowana częstotliwość, składająca się z suma poprzedniej częstotliwości oraz częstotliwości danych, które należy wziąć pod uwagę.

Ta kolumna zaczyna się od pierwszej kolumny kolumny częstotliwości bezwzględnej, w tym przypadku wynosi 0. Dla następnej wartości jest to dodawane z poprzednim. Zatem ostatnie dane zgromadzonej częstotliwości są kontynuowane, co musi pokryć się z danymi całkowitych.

Tabela Frecuency

Poniższa tabela pokazuje zmienną „Liczba telefonów sprzedawanych w ciągu jednego dnia”, jej bezwzględna częstotliwość i szczegółowe obliczenie jej skumulowanej częstotliwości.

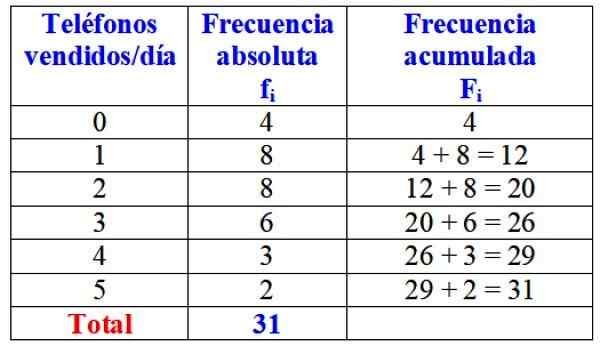Tabela bezwzględnych i zgromadzonych częstotliwości dla zmiennych „telefonów sprzedawanych dziennie”. Źródło: f. Zapata.

Na pierwszy rzut oka można powiedzieć, że dana marka jest prawie zawsze sprzedawana jeden lub dwa telefony dziennie, ponieważ najbardziej bezwzględna częstotliwość to 8 dni, co odpowiada tym wartościom zmiennej. Tylko przez 4 dni miesiąca nie sprzedawałem ani jednego telefonu.

Może ci służyć: Przyczyny trygonometryczne: Przykłady, ćwiczenia i zastosowania

Jak wspomniano, łatwiej jest zbadać tabelę niż pierwotnie zebrane dane.

Skumulowany rozkład częstotliwości

Skumulowany rozkład częstotliwości to tabela, w której dostępne są częstotliwości bezwzględne, nagromadzone częstotliwości, skumulowane częstotliwości względne i akumulowane częstotliwości procentowe.

Podczas gdy zauważana jest zaleta zorganizowania danych w tabeli takiej jak poprzednia, jeśli numer danych jest bardzo duży, możliwe jest, że nie wystarczy je uporządkować, jak pokazano powyżej, ponieważ jeśli pojawi się wiele częstotliwości, nadal jest to trudne interpretować.

Problem można zaradzić, budując Rozkład częstotliwości W odstępach przydatnej procedury, gdy zmienna przyjmuje dużą liczbę wartości lub jeśli jest to zmienna ciągła.

Tutaj wartości są pogrupowane w odstępy o równej amplitudzie, zwane klasa. Zajęcia charakteryzują się posiadaniem:

-Limit klasy: to ekstremalne wartości każdego przedziału, są dwa, górna granica i dolna granica. Zasadniczo górna granica nie należy do interwału, ale do natychmiastowej obserwującej, podczas gdy dolna granica należy.

-Marka klas: Jest to punkt środkowy każdego przedziału i jest traktowany jako jego reprezentatywna wartość.

-Szerokość klasy: Oblicza się go odejmując wartość głównego i najmniejszego (zakres) i podzielenie przez liczbę klas:

Szerokość klasy = zakres / liczba klas

Następnie szczegółowo opisano opracowanie rozkładu częstotliwości.

Przykład

Ten zestaw danych odpowiada 40 klas egzaminu matematycznego, w skali od 0 do 10:

0; 0; 0; 1; 1; 1; 1; 2; 2; 2; 3; 3; 3; 3; 4; 4; 4; 4; 5; 5; 5; 5; 6; 6; 6; 6; 7; 7; 7; 7; 7; 7; 8; 8; 8; 9; 9; 9; 10; 10.

Można opracować rozkład częstotliwości z określoną ilością klas, na przykład 5 klas. Należy pamiętać, że podczas korzystania z wielu klas dane nie są łatwe do interpretacji, a poczucie realizacji grupy jest utracone.

Może ci służyć: ile musisz dodać do 3/4, aby uzyskać 6/7?

A jeśli wręcz przeciwnie, są zgrupowane w bardzo niewielu, wówczas informacje są rozcieńczone, a część ich utraty. Wszystko zależy od ilości posiadanych danych.

W tym przykładzie dobrym pomysłem jest posiadanie dwóch wyników w każdym przedziale, ponieważ powstanie 10 wyników i 5 klas. Ranga jest odejmowaniem między główną a najmniejszą oceną, przy czym szerokość klasy:

Szerokość klasy = (10-0)/5 = 2

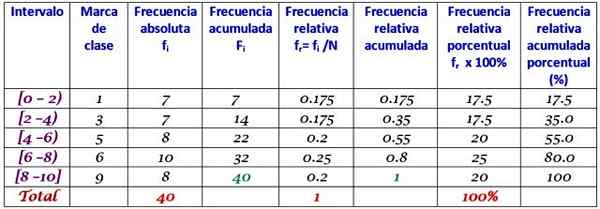
Interwały są zamknięte przez lewą i otwarte po prawej (z wyjątkiem ostatniego), które są symbolizowane odpowiednio za pomocą kwadratowych nawiasów i nawiasów. Wszystkie mają tę samą szerokość, ale nie jest obowiązkowa, chociaż najczęstsze.

Każdy przedział zawiera pewną ilość elementów lub częstotliwość bezwzględną, aw następnej kolumnie jest zgromadzona częstotliwość, w której suma jest przenoszona. Tabela pokazuje również częstotliwość względną F_R  (Bezwzględna częstotliwość między całkowitą liczbą danych) a procentowym procentem częstotliwości f_R × 100%.

Proponowane ćwiczenie

Firma codziennie rozmawiała z klientami w ciągu pierwszych dwóch miesięcy roku. Dane są następujące:

6, 12, 7, 15, 13, 18, 20, 25, 12, 10, 8, 13, 15, 6, 9, 20, 24, 12, 7, 10, 11, 13, 9, 12, 15, 18, 20, 13, 17, 23, 25, 14, 18, 6, 14, 16, 9, 6, 10, 12, 13, 17, 14, 26, 7, 12, 24, 7, 7

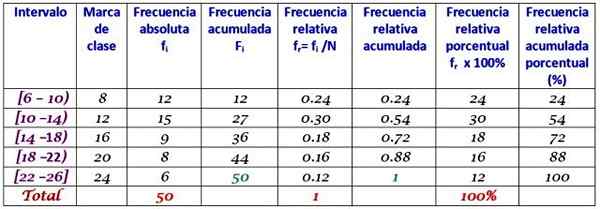
Grupuj w 5 klasach i zbuduj tabelę z rozkładem częstotliwości.

Odpowiedź

Szerokość klasy to:

(26-6)/5 = 4

Spróbuj go rozwiązać przed zobaczeniem odpowiedzi.

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
4. Prawdopodobieństwo i statystyka. Szerokość interwału klasowego. Pobrano z: Pedroprobababagality i stadystyczne.Blogspot.com.
5. Spiegel, m. 2009. Statystyka. Seria Schaum. 4 Ta. Wydanie. McGraw Hill.
6. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.