Wzór bezwzględnej częstotliwości, obliczenia, rozkład, przykład

Absolutna frecuencja Jest zdefiniowany jako liczba czasów, w których te same dane są powtarzane w zestawie obserwacji zmiennej numerycznej. Suma wszystkich bezwzględnych częstotliwości jest równoważna sumę danych.

Gdy istnieje wiele wartości zmiennej statystycznej, wygodne jest ich właściwe zorganizowanie ich w celu wyodrębnienia informacji o ich zachowaniu. Takie informacje są podawane przez centralne miary tendencji i miary dyspersji.

Rysunek 1. Bezwzględna częstotliwość obserwacji statystycznej jest kluczem do znalezienia trendu, który następuje po zestawie danych

W obliczeniach tych miar dane są reprezentowane przez częstotliwość, z jaką pojawiają się we wszystkich obserwacjach.

Poniższy przykład pokazuje, jak ujawnianie bezwzględnej częstotliwości każdego danych jest. W pierwszej połowie maja były to rozmiary najlepszych kostiumów koktajlowych, dobrze znanego magazynu odzieżowego:

8; 10; 8; 4; 6; 10; 12; 14; 12; 16; 8; 10; 10; 12; 6; 6; 4; 8; 12; 12; 14; 16; 18; 12; 14; 6; 4; 10; 10; 18

Ile sukienek jest sprzedawanych w określonym rozmiarze, na przykład rozmiar 10? Właściciele są zainteresowani wiedzą o wydawaniu zamówień.

Zamawianie danych jest łatwiejsze do zliczenia, w sumie jest dokładnie 30 obserwacji, niż zamówione od najmniejszych do najwyższych jest takie:

4; 4; 4; 6; 6; 6; 6; 8; 8; 8; 8; 10; 10; 10; 10; 10; 10; 12; 12; 12; 12; 12; 12; 14; 14; 14; 16; 16; 18; 18

A teraz jest oczywiste, że rozmiar 10 jest powtarzany 6 razy, dlatego jego bezwzględna częstotliwość jest równa 6. Ta sama procedura jest przeprowadzana w celu znalezienia bezwzględnej częstotliwości pozostałych rozmiarów.

[TOC]

Formuły

Częstotliwość bezwzględna, oznaczona jako F_Siema, Jest równy liczbie czasów jako pewnej wartości x_Siema znajduje się w grupie obserwacji.

Zakładając, że całkowite obserwacje mają n wartości, suma wszystkich częstotliwości bezwzględnych musi być równa wspomnianej liczbie:

Może ci służyć: papomudas

∑F_Siema = f₁ + F₂ + F₃ +… F_N = N

Inne częstotliwości

Jeśli każda wartość F_Siema Jest dzielony przez całkowitą liczbę danych N, masz Częstotliwość względna F_R wartości x_Siema:

F_R = f_Siema / N

Częstotliwości względne to wartości między 0 a 1, ponieważ n jest zawsze większe niż dowolne f_Siema, Ale suma musi być równa 1.

Mnożenie przez 100 do każdej wartości f_R masz Względna częstotliwość procentowa, którego suma wynosi 100%:

Względna częstotliwość procentowa = (f_Siema / N) x 100%

To również ważne zgromadzona częstotliwość F_Siema Do pewnej obserwacji jest to suma wszystkich bezwzględnych częstotliwości, dopóki nie wspomniana obserwacja obejmuje:

F_Siema = f₁ + F₂ + F₃ +… F_Siema

Jeśli zgromadzona częstotliwość jest podzielona przez całkowitą liczbę danych N, masz nagromadzona częstotliwość względna, to pomnożone na 100 powoduje w skumulowany procent częstotliwości względnej.

Jak uzyskać absolutną częstotliwość?

Aby znaleźć bezwzględną częstotliwość pewnej wartości, która należy do zestawu danych, wszystkie z nich są zorganizowane od najmniej do największej.

W przykładzie rozmiarów sukienek bezwzględna częstotliwość rozmiaru 4 to 3 sukienki, czyli F₁ = 3. W rozmiarze 6 sprzedano 4 sukienki: F₂ = 4. W rozmiarach 8 4 sukienki były również sprzedawane, F₃ = 4 i tak dalej.

Tabelacja

Całkowite wyniki mogą być reprezentowane w tabeli, która pokazuje bezwzględne częstotliwości każdego:

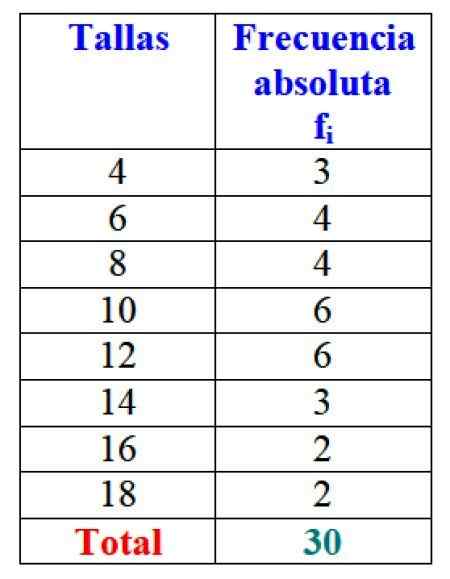Rysunek 2. Tabela reprezentująca zmienną „sprzedawaną” i odpowiednie bezwzględne częstotliwości. Źródło: f. Zapata.

Oczywiście korzystne jest zamówienie informacji i dostęp do nich, zamiast pracować z luźnymi danymi.

Ważny: Zauważ, że dodając wszystkie wartości kolumny F_Siema  Całkowita liczba danych jest zawsze uzyskiwana. Jeśli nie, rachunkowość musi zostać sprawdzona, ponieważ wystąpi błąd.

Rozszerzona tabela częstotliwości

Poprzednia tabela można rozszerzyć, dodając inne typy częstotliwości w kolejnych kolumnach po prawej stronie:

Może ci służyć: Homocedastyczność: co to jest, znaczenie i przykłady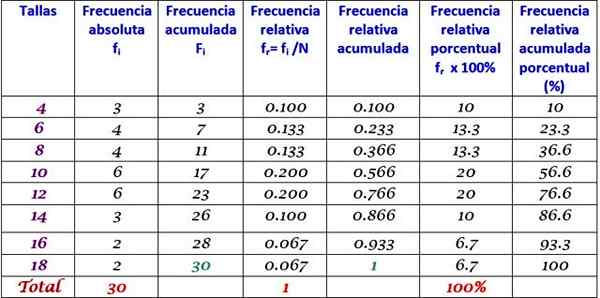

Rozkład częstotliwości

Rozkład częstotliwości jest wynikiem organizacji danych pod względem ich częstotliwości. Podczas pracy z wieloma danymi wygodne jest grupowanie ich na kategorie, interwały lub klasy, każda z odpowiednimi częstotliwościami: bezwzględne, względne, nagromadzone i procentowe.

Celem ich wykonania jest łatwiejszy dostęp do informacji, które zawierają dane, a także poprawnie ich interpretacja, co nie jest możliwe, gdy są one prezentowane bez kolejności.

W przykładzie rozmiarów dane nie są zgrupowane, ponieważ nie są to zbyt wiele rozmiarów i można je łatwo manipulować i policzyć. Zmienne jakościowe można również opracować w ten sposób, ale gdy dane są bardzo liczne, działają lepiej grupując je na zajęciach.

Rozkład częstotliwości dla zgrupowanych danych

Aby zgrupować dane w klasach o równej wielkości, należy wziąć pod uwagę następujące:

-Rozmiar, szerokość lub amplituda klasy: Jest to różnica między największą wartością klasy a mniejszymi.

Rozmiar klasy decyduje się na podzielenie zakresu R przez liczbę klas do rozważenia. Zakres jest różnicą między maksymalną wartością danych a mniejszymi, takimi jak ten:

Rozmiar klasy = zakres / liczba klas.

-Limit klasy: przedział, który przechodzi od dolnej granicy do górnej granicy klasy.

-Marka klas: Jest to punkt środkowy interwału, który jest uważany za reprezentatywny dla klasy. Jest obliczany za pomocą pół -limitu górnego granicy i dolnej granicy klasy.

-Liczba klas: Można użyć formuły Sturges:

Klasy = 1 + 3322 log n

Gdzie n jest liczbą klas. Jak zwykle liczba dziesiętna, następujące są zaokrąglone.

Przykład

Duża maszyna fabryczna nie działa, ponieważ ma powtarzające się awarie. Kolejne okresy bezczynności w ciągu kilku minut, wspomnianej maszyny, są zapisane poniżej, z łączną liczbą 100 danych:

Może ci służyć: prawdopodobieństwo częstotliwości: koncepcja, jak jest obliczane i przykłady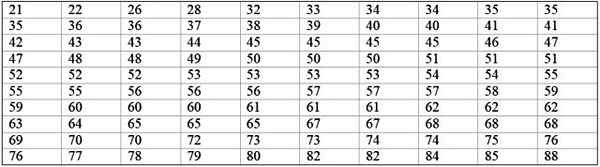

Najpierw ustalono liczbę klas:

Klasy = 1 + 3322 log n = 1 + 3.32 log 100 = 7.64 ≈ 8

Rozmiar klasy = zakres / liczba klas = (88-21) / 8 = 8.375

Jest to również liczba dziesiętna, więc wymaga 9 jako rozmiar klasy.

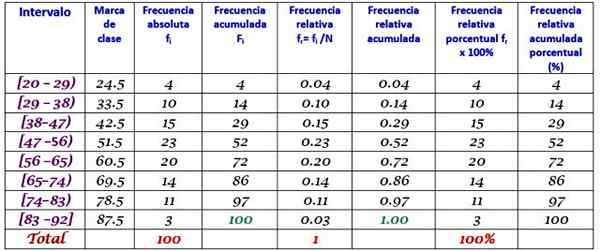
Marka klasowa jest średnią między górną i dolną granicą klasy, na przykład dla klasy [20-29), istnieje znak:

Marka klas = (29 + 20) / 2 = 24.5

Kontynuuj w ten sam sposób, aby znaleźć marki klasowe pozostałych odstępów.

Ćwiczenie rozwiązane

40 młodych ludzi wskazało, że w minutach, które minęły w Internecie w ostatnią niedzielę, był następny, zamówiony coraz bardziej:

0; 12; 20; 35; 35; 38; 40; Cztery pięć; 45, 45; 59; 55; 58; 65; 65; 70; 72; 90; 95; 100; 100; 110; 110; 110; 120; 125; 125; 130; 130; 130; 150; 160; 170; 175; 180; 185; 190; 195; 200; 220.

Poproszono o zbudowanie rozkładu częstotliwości tych danych.

Rozwiązanie

Ranga R zestawu n = 40 danych wynosi:

R = 220 - 0 = 220

Zastosowanie wzoru Sturges w celu ustalenia liczby klas daje następujący wynik:

Klasy = 1 + 3322 log n = 1 + 3.32 log 40 = 6.3

Podobnie jak dziesiętstwo, bezpośrednia całość wynosi 7, dlatego dane są pogrupowane w 7 klas. Każda klasa ma szerokość:

Rozmiar klasy = zakres / liczba klas = 220/7 = 31.4

Wartość zbliżona i okrągła wynosi 35, dlatego wybiera się szerokość klasy 35.

Znaki klasowe są obliczane uśrednienie górnej i dolnej granicy każdego przedziału, na przykład dla przedziału [0,35):

Marka klas = (0+35)/2 = 17.5

Kontynuujemy w ten sam sposób z pozostałymi klasami.

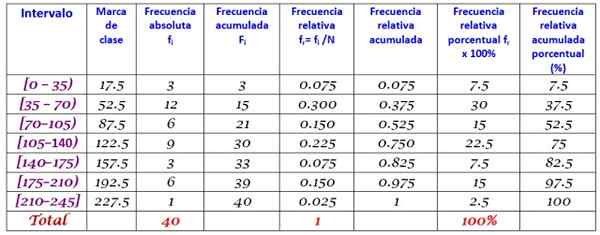
Wreszcie częstotliwości są obliczane zgodnie z procedurą opisaną powyżej, co skutkuje następującym rozkładem:

Bibliografia

1. Berenson, m. 1985. Statystyka administracji i ekonomii. Inter -American s.DO.
2. Devore, J. 2012. Prawdopodobieństwo i statystyki inżynierii i nauki. 8. Wydanie. Cengage.
3. Levin, r. 1988. Statystyki dla administratorów. 2. Wydanie. Prentice Hall.
4. Spiegel, m. 2009. Statystyka. Seria Schaum. 4 Ta. Wydanie. McGraw Hill.
5. Walpole, r. 2007. Prawdopodobieństwo i statystyki inżynierii i nauki. osoba.