Współczynnik pakowania

Współczynnik pakowania jest ułamkiem wskazującym, ile objętości zajmują cząstki, czy to atomy, jony czy cząsteczki, w wewnętrznej przestrzeni kryształu. Jego wartość jest zawsze mniejsza niż 1, co staje się 100% objętości szkła; Dokładnie, jego jednolita komórka, która jest najmniejszą reprezentacją całego szkła.

Współczynnik pakowania 100% oznacza, że ​​cząstki zajmują objętość jednolitej komórki w całości. Fizycznie nie jest w stanie tak się stało, ponieważ oznaczałoby na przykład, że atomy deformują ich radiotelefony i rozpuszczają się tak, jakby były „płynem elektronicznym”. Geometria atomów, sferyczna dla wygody, zawsze powoduje puste przestrzenie podczas opakowania.

Jak dzieje się to w słodkich maszynach dozujących, współczynnik opakowania mówi nam, jak „ciasne” są cząstki kryształu: im większa jest, tym więcej gumy lub atomów będzie w kosmosie

W definicji współczynnika opakowania zakłada się, że atomy składają się z sztywnych kulek, takich jak guma lub kule cukierkowe z urządzenia wydawanego (obraz doskonały). Wśród sfer zawsze będą puste przestrzenie, w których można zakradać mniejsze kule (zanieczyszczenia lub dodatki).

Jeśli zwiększymy współczynnik opakowania, kule zostaną ściskane, obracając najbardziej zwarte i gęste szkło; lub z drugiej strony bardziej odkształcalne, jak w przypadku metali plastycznych i plastycznych.

Współczynnik opakowania dotyczy dowolnego rodzaju szkła. Jednak jego obliczenia mogą stać się nieco żmudne, więc będą rozważane tylko dla kryształów atomowych o prostych strukturach.

[TOC]

Formuła współczynnika pakowania

Współczynnik pakowania jest zwykle wyrażany jako wartości procentowe. Na przykład, jeśli jego wartość wynosi 40%, oznacza to, że cząstki ledwo zajmują 40% całkowitej przestrzeni komórki jednostkowej; lub co to samo, co stwierdzenie, że 60% szkła jest „pustych”.

Powyższe wyjaśnia, jaki jest wzór do obliczenia tego czynnika:

• Ugly = (objętość atomów)/ (objętość komórki jednostkowej)

Gdzie brzydkie oznacza Współczynnik pakowania atomowego, Jakie są najprostsze kryształy.

Objętość komórki jednostkowej zależy od jej parametrów (takich jak długość jej boków), z którymi jest ona kontynuowana przez prostą geometrię w celu obliczenia jej objętości. Z drugiej strony atomy to te, które definiują komórkę, więc możliwe jest wyrażanie wymiarów tego samego z radia atomowych, co będzie widać w następnych sekcjach.

Może ci służyć: Racemic Mix: Chiralność, przykłady

W odniesieniu do objętości atomów całkowita liczba z nich jest obecna w komórce jednostkowej (1, 2, 3 itp.), a także jej geometria sferyczna. Dlatego formuła jest nieco modyfikowana:

Ugly = (atomy Nº) (objętość atomu)/ (objętość komórki jednostkowej)

Aby obliczyć brzydkie, musisz ustalić, a następnie nie., V_atom i v_{Jednolita komórka}.

Prosty sześcien

Prosta komórka jednostkowa sześcienna. Źródło: ccc_crysta_cell_ (nieprzezroczyste).SVG: *COBIKE_CENTRE_ATOMES_PAR_MAILLE.SVG: CDang (oryginalna idea i wykonanie SVG), Samuel Dupré (3D Odeeling with Solidworks) Wyprowadza pracę: Daniele Pugliesi (Talk) Dinive Prace: Daniele Pugliesi, CC By-Sa 3.0, Via Wikimedia Commons

Najprostszą jednolitową komórką jest prosta sześcienna. W nim mamy pewne części atomów w każdym z narożników. Jeśli zobaczymy, zauważymy, że długość Do Z tej komórki wynosi 2R, ponieważ to atomy definiują komórkę. Tak więc objętość komórki jednostkowej będzie równa:

V_{Jednolita komórka} = Do³ (objętość kostki)

= (2r)³

= 8r³

Tymczasem objętość atomu będzie równa:

V_atom = (4/3) πr³ (objętość kuli)

Każdy z narożników jest wspólny przez kolejne 8 sąsiednich komórek jednostkowych. Dlatego mamy ułamek 1/8 w każdym rogu, a mając 8 z nich, nie obchodzi nas 1 atom na komórkę jednostkową (1/8 x 8 = 1).

Współczynnik pakowania to:

Ugly = (1) (4/3) πr³ /8r³

= π/6 ≈ 52%

To znaczy w prostej komórce sześciennej atomy zajmują 52% całej objętości szkła.

Sześcienne skupione w ciele

Określenie objętości komórki

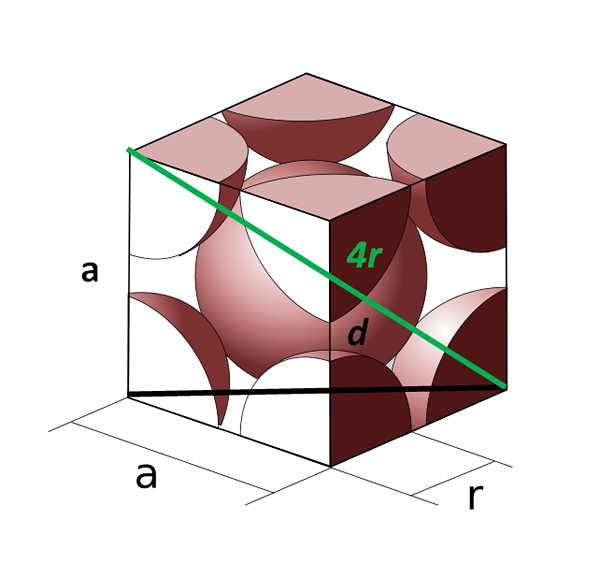
Jednolentna komórka ciała skoncentrowana na ciele. Źródło: Cobique_Centre_atomes_Par_maille.SVG: CDANG (oryginalna idea i wykonanie SVG), Samuel Dupré (3D Odeeling z Solidworks) Prace pochodne: Daniele Pugliesi, CC By-Sa 3.0, Via Wikimedia Commons

Teraz zobaczmy komórkę sześcienną wyśrodkowaną na ciele. Strona Do Nie może już być równy 2R, ponieważ mamy pustą przestrzeń między dwoma atomami narożników. Istnieje zatem przekątna D równe 4R (kolor zielony), który przecina komórkę przez środek i dotyka przeciwnych narożników i kolejnego przekątnego D twarzy (czarny).

Strony Do, D a 4r narysuj trójkąt prostokąta, do którego możemy zastosować trygonometrię, aby obliczyć, jaka jest wartość Do:

(4r)² = d² + Do²

Może ci służyć: siły międzycząsteczkowe

Ale z drugiej strony u podstawy komórki jednostkowej mamy inny trójkąt (Do, Do I D), do którego możemy obliczyć hipotencję:

D²  = a² + Do²

= 2a²

Wymiana wtedy będziemy mieli:

(4r)² = (2²) + a²

(4r)² = 3a²

A = (4/√3) r

V_{Jednolita komórka} jest równe:

V_{Jednolita komórka} = a³

= ((4/√3) r)³

Określenie współczynnika opakowania

Zauważ, że w odniesieniu do liczby atomów mamy 1 atom w tej komórce, po tym samym odliczeniu wykonanym dla prostej komórki sześciennej i kolejny dodatkowy atom, który znajduje się na środku komórki. Zatem istnieje 2 atomy dla każdej komórki sześciennej wyśrodkowanej na ciele.

Współczynnik pakowania jest zatem:

Ugly = (2) (4/3) πr³ / ((4/ √3) r)³

= (√3/8) π ≈ 68%

Oznacza to, że w komórce sześciennej skoncentrowanej na ciele 68% objętości szkła zajmuje atomy. W związku z tym ten krystaliczny układ jest bardziej zwarty (lub gęsty) niż proste sześcienne.

Sześcienne skupione na twarzach

Określenie objętości komórki

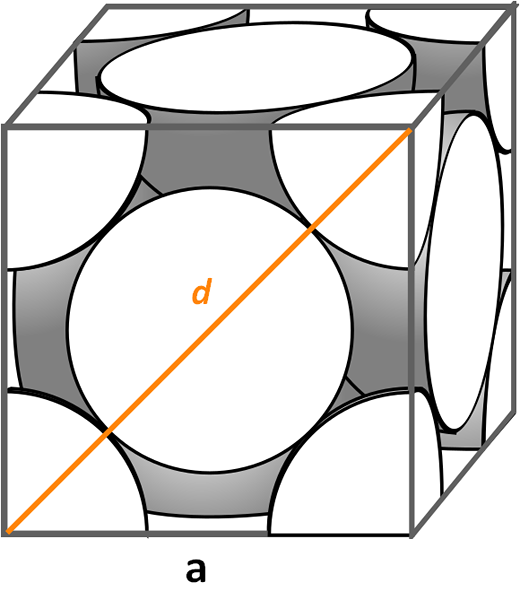
Sześcienna jednolita komórka skoncentrowana na twarzach. Źródło: Cdang, CC BY-SA 3.0, Via Wikimedia Commons

Spójrzmy na sześcienną jednolitą komórkę skoncentrowaną na twarzach, bardzo powszechnych w symfinach soli nieorganicznych i niektórych metalach, takich jak złoto i srebro. Aby określić jego współczynnik opakowania, musimy zacząć, zgodnie z poprzednimi przykładami, aby znaleźć, jaka jest objętość jej komórki jednostkowej. Konieczne jest ponownie obliczenie strony Do I tak objętość kostki Do³.

Tym razem procedura jest łatwiejsza i bardziej bezpośrednia, ponieważ mamy przekątną D Z przodu, wraz z bokami Do, Tworzą prawy trójkąt, do którego możemy zastosować trygonometrię:

D² = a² + Do²

= 2a²

Clearing Do będziemy mieli:

Do = D/√2

Ale wizualnie to zauważamy D Jest to równe 4R, więc dokonujemy substytucji:

Do = 4r/√2

= 2R 2^1-1/2

= (2√2) r

Bycie v_{Jednolita komórka} równy:

Do³ = ((2√2) r)³

= (16√2) r³

Jeśli chodzi o liczbę atomów na komórkę, mamy osiem części jednego atomu w każdym rogu, a także połowę atomu dla każdej z sześciu twarzy, które są wspólne dla innej sąsiedniej komórki. Dlatego liczba atomów jest równa:

Atomy Nº = 1/8 (8) + 1/2 (6) = 1 + 3 = 4

Określenie współczynnika opakowania

Mając to na 4 atomy w każdej komórce sześciennej skupione na twarzach, a także jej objętość, która jest równa (16√2) r³, Następnie możemy obliczyć współczynnik pakowania:

Ugly = (atomy Nº) (objętość atomu)/ (objętość komórki jednostkowej)

= (4) (4/3) πr³ / (16√2) r³

Może ci służyć: grupa Acilo: Struktura, cechy, związki i pochodne

= π/(3√2) ≈ 74%

Należy zauważyć, że ta komórka jest jeszcze bardziej zwarta niż poprzednie: 74% całkowitej objętości komórki jest zajęte przez atomy. W idealnym i czystym kryształu byłoby to równoważne, że 26% jego wolumenu jest dostępnych dla organizacji innych atomów gości.

Kompaktowy sześciokąta

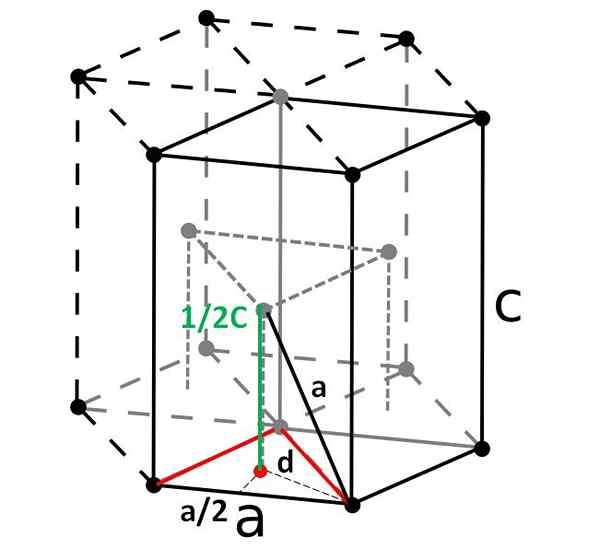
Kompaktowa komórka sześciokątna i jej romboedralna komórka prymitywna. Źródło: Original: Dornelfvector: DePiep, CC BY-SA 3.0, Via Wikimedia Commons

Wreszcie, wśród najprostszych i najbardziej kompaktowych komórek jednostkowych mamy kompaktowe sześciokątne. W przeciwieństwie do poprzednich obliczenia jego objętości jest nieco bardziej uciążliwe. Jak widać, nie jest sześcienne, więc ma dwa parametry Do I C, Ten ostatni jest wysokością komórki.

Określenie wysokości komórki

Komórkę sześciokątną można podzielić na trzy komórki Rhomboyan, a z jednego z nich zostanie obliczone Do I C. Strona Do, Chociaż nie jest tak widoczne na powyższym obrazku, jest to równe 2R. Liczyć C, Zamiast tego używamy trójkąta i produktu czerwonego punktu wewnętrznego trójkątnego pryzmatu tej samej komórki.

Musimy obliczyć odległość D Aby móc ustalić, ile to jest warte C. Na podłodze czerwony trójkąt jest równoboczny, z kątem 60º. Ale jeśli inny wewnętrzny trójkąt prostokąta jest rozważany z bokami Do/2 i D, i kąt 30º (połowa), a następnie za trygonometrię możemy określić D:

Cos (30º) = (Do/2) / D

D = Do/√3

A teraz uważamy odpowiedni trójkąt złożony z boków C/2 (zielony), Do (czarny i D (kropkowany):

Do² = (Do/√3)² + (C/2)²

Clearing C Mielibyśmy:

C = √ (8/3) Do

I zastępowanie Do Do 2r:

C = √ (8/3) (2r)

= √ (4 · 2/3) (2R)

= 4√ (2/3) r

Określenie objętości komórki

Aby określić objętość komórki sześciokątnej, musisz pomnożyć obszar sześciokąta przez jego wysokość. Wiedząc, że trójkąty równoboczne mają strony Do, jego wysokość jest obliczana H. Zatem znalezienie obszaru trójkąta, który jest dla tego przypadku √3/4Do², Mnożymy tę wartość przez 6, aby uzyskać obszar sześciokąta: 3 (√3/2)Do²

Objętość jest zatem:

V_{Jednolita komórka} = Wysokość obszaru sześciokątnego x

= 3 (√3/2)Do² X 4√ (2/3) r

I zastąpienie jeszcze raz Do Do 2r:

V_{Jednolita komórka}  = 3 (√3/2) (2R)² X 4√ (2/3) r

= 24√2 r³

Określenie współczynnika opakowania

W komórce sześciokątnej w zakątkach znajduje się 12 atomów, które mają w środku 1/6. Istnieją również 3 wewnętrzne atomy, których objętości są kompletne, a kolejne 2 atomy na górnych i dolnych twarzach, których połowa jego objętości znajduje się wewnątrz komórki.

Dlatego liczba atomów jest równa:

Nº ATOM = 1/6 (12) + 1 (3) + 1/2 (2) = 6 atomów

A współczynnik pakowania jest wreszcie:

Ugly = (atomy Nº) (objętość atomu)/ (objętość komórki jednostkowej)

= (6) (4/3) πr³ / 24√2 r³

= π/(3√2) ≈ 74%

Zauważ, że współczynnik przedziału dla komórki sześciokątnej jest taki sam jak w przypadku komórki sześciennej wyśrodkowanej na twarzach. To znaczy, oba są równie kompaktowe.

Bibliografia

1. C. Barry Carter i m. Grant Norton. (2007). Nauka i inżynieria materiałów ceramicznych. Skoczek.
2. Shiver & Atkins. (2008). Chemia nieorganiczna. (Czwarta edycja). MC Graw Hill.
3. Whitten, Davis, Peck i Stanley. (2008). Chemia. (8 wyd.). Cengage Learning.
4. Wikipedia. (2021). Współczynnik pakowania atomowego. Źródło: w:.Wikipedia.org
5. Brandon. (2021). Co to jest współczynnik pakowania atomowego (i jak go obliczyć dla SC, BCC, FCC i HCP)? Student nauk o materiałach i inżynierii. Odzyskane z: Msestudent.com