Ocena funkcji

Aby ocenić funkcję, której znany jest schemat, dla określonej wartości lub elementu zestawu początkowego, wystarczy obserwować odpowiedni element w zestawie przybyszu. Źródło: f. Zapata.

Jaka jest ocena funkcji?

Ocena funkcji Polega na określaniu obrazu określonej wartości domeny. Innymi słowy, dla danej wartości zestawu początkowego musisz znaleźć odpowiadające mu w zestawie przyjazdu.

Funkcję może być reprezentowana na kilka sposobów. Jeśli, na przykład, schemat Venna jest dostępny, ocena jest bardzo prosta, wystarczy wybrać element zestawu początkowego lub domeny i zobaczyć element odpowiadający zestawie przybycia.

Na schemacie „…… to kapitał…”, reprezentowany powyżej, podczas oceny tej funkcji w elemencie „Kanada” jest to element „Ottawa”, w przypadku zrobienia tego z „Meksykiem”, jest to „Meksyk” i Wkrótce.

Jeśli funkcja jest podana w postaci uporządkowanych par, ocena jest również prosta: drugim członkiem uporządkowanego momentu obrotowego jest obraz pierwszego członka. Na przykład z funkcją f (x) opisaną przez:

f (x) = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Podczas oceny funkcji dla wartości 3 wynik wynosi 6; Podczas oceny za 5 jest to 10 i tak dalej.

Podobnie, funkcję można ocenić, gdy wykres jest dostępny, pod warunkiem, że wartość, którą chcesz ocenić, pojawia się w nim.

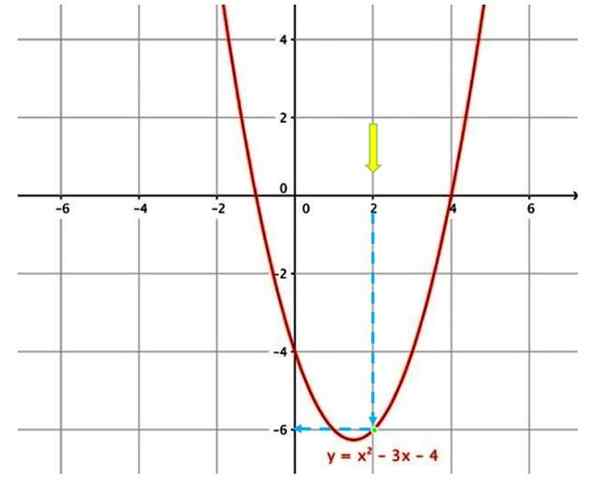Wykres oceny funkcji

Na przykład, aby ocenić powyższą funkcję, przy x = 2, pierwszą rzeczą jest zlokalizowanie na wykresie a x = 2 (żółta strzałka).

Następnie musisz poruszać się po niebieskiej strzałce pionowej, aż dotkniesz krzywej (zielony punkt). Postępuj ponownie zgodnie z niebieską strzałką, która wskazuje odpowiednią wartość na osi pionowej, a zatem przy ocenie funkcji przy x = 2, y = −6 uzyskuje się.

Może ci służyć: funkcje trygonometryczne: podstawowy, w płaszczyźnie kartezjańskim, przykłady, ćwiczenia

Oceń daną funkcję w notacji matematycznej

W dolnej części powyższej wykresu pojawia się funkcja graficzna, ale podana w notacji matematycznej, to znaczy poprzez wzór:

f (x) = x² - 3x - 4

Jeśli chcesz ocenić funkcję w dowolnej wartości x = a, musisz znaleźć f (a), który jest po prostu odczytany „f A”.

Aby znaleźć wynik, x = A jest zastąpione w formule funkcji, a żądane operacje i obliczenia są przeprowadzane tam.

Załóżmy, że chcesz ocenić funkcję przykładu na x = −1. Oznacza to, że należy znaleźć F (−1).

Pierwszym krokiem jest zastąpienie x = -1 w funkcji:

f (−1) = (−1)² - 3 ∙ (-1) - 4

A następnie wykonaj wskazane operacje, które w tym przykładzie to:

• Znajdź kwadrat -1: (-1)² = 1
• Odejmij poprzednią wartość produktu 3 ∙ (-1): 3 ∙ (-1) = −3
• Od poprzedniego wyniku odejmij 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

Czytelnik może potwierdzić ten wynik, z wykresu funkcji.

Opisaną procedurę można zastosować do oceny funkcji w dowolnej innej wartości domeny. Na przykład można znaleźć f (-2), f (100) lub nawet f (h), gdzie h jest dowolną wartością zmienną, która należy do domeny funkcji.

Oceń funkcję o wartości x = h 

Załóżmy, że chcesz ocenić funkcję o jakiejś dowolnej wartości, częste działanie w obliczeniach matematycznych.

W takim przypadku x jest zastępowane przez H, w taki sam sposób, w jaki jest wykonywany, gdy x przyjmuje dowolną wartość numeryczną, a wynik jest uproszczony jak najwięcej.

Gdy wynikowej operacji nie można już uprościć, pozostała wynikowa operacja.

Może ci służyć: ENEGON: Właściwości, jak zrobić engon, przykłady

Przykład

Chcesz ocenić funkcję f (x) = x² - 3x - 4 przy x = h+1. Niezbędne podejście jest następujące:

f (H+1) = (H+1)² - 3 ∙ (H+1) - 4

Po prawej stronie równości pierwszy termin jest niezwykłym produktem:

(H+1)² = h² +2H + 1

Poniższy termin jest rozwiązywany za pośrednictwem nieruchomości dystrybucyjnej:

3 ∙ (H + 1) = 3H + 3

Podczas wymiany wszystkich powyższych masz:

f (H+1) = (H+1)² - 3 ∙ (H+1) - 4 = h² +2H + 1 - (3H + 3) - 4

Podobne terminy są zmniejszone o sumę algebraiczną:

f (h+1) = h² + 2H + 1 - 3H - 3 - 4 = h² - H - 6

Niedoornik różnicowy

Różnicowy iloraz lub stosunek różnic d funkcji f (x) jest zdefiniowany jako:

Ze stanem h ≠ 0, co jest konieczne, ponieważ podział na 0 nie jest zdefiniowany.

Ten iloraz jest interpretowany geometrycznie jako nachylenie linii sekundowej do krzywej, to znaczy linii, która przechodzi przez dwa punkty. Współrzędne tych punktów to: [x, f (x)] i [x+h; f (x+h)], jak widać na poniższym rysunku:

Igunowy zróżnicowany jest równoważny obliczaniu nachylenia linii sekundowej na krzywą, która przechodzi przez wskazane punkty. Źródło: Wikimedia Commons.

Dlatego ten iloraz pojawia się w obliczaniu pochodnej funkcji, ponieważ podchodząc do wartości „H”, linia sekutacji staje się linią styczną w punkcie (x, y), ponieważ punkty w przecięciu przecinania Figura jest tak blisko, że mają ten sam punkt.

Zatem linia staje się styczna (przechwytuje krzywą w jednym punkcie).

Jest to dokładnie definicja pochodzącej z funkcji: nachylenie stycznej linii do krzywej w punkcie współrzędnym (x, f (x)))))).

Może ci służyć: Media ważone: jak jest obliczane, przykłady i ćwiczenia

Jak widać, iloraz różnicowy wymaga oceny funkcji w (x + h) i w x. Poniższe przykłady ilustrują, jak to zrobić.

Przykład 1

Chcesz znaleźć różnicowy iloraz funkcji f (x) = 2x - 3. Pierwszym krokiem jest podniesienie oceny funkcji dla x = x + h, jak to:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Następnie wynik jest zastępowany w definicji D, podano wcześniej:

Z h ≠ 0.

Licznik jest uproszczony, jak to możliwe, zmniejszając podobne warunki:

Wreszcie, wspólne czynniki w licznikach i mianowniku są uproszczone:

D = 2

Przykład 2

Znajdź różnicowy iloraz funkcji f (x) = x² - 3x - 4.

Postępujemy jak w poprzednim przykładzie, znalezienie pierwszego f (x+h), zastępując wynik d i upraszczanie maksimum:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2HX + H² - 3x - 3H - 4

= 2x+H-3

Dlatego:

D = 2x+H-3

Gdzie h ≠ 0.

Rozwiązane ćwiczenia

Ćwiczenie 1

Oceń funkcję f (x) = 2x² - 4x + 1 Kiedy:

a) x = -1
b) x = 0
c) x = 2

Rozwiązanie

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Rozwiązanie b

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Rozwiązanie c

f (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8–8 + 1 = 1

Ćwiczenie 2

Zespół ekologów ustalił, że funkcja w (t) = 0.Lt² + 1.8t służy modelowaniu ilości odpadów „w”, w kilogramach, które są wrzucane do określonej rzeki, w czasie „t”, podawanym w ciągu dni.

Oblicz ilość odpadów wyrzuconych do rzeki na końcu:

a) 3 dni
b) 1 tydzień
c) 1 miesiąc

Rozwiązanie

W (t) Funkcja jest oceniana po t = 3 dni:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilogramy

Rozwiązanie b

Przed oceną musisz spędzić 1 tydzień do dni:

1 tydzień = 7 dni

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilogramów

Rozwiązanie c

Ponownie konieczne jest przekształcenie miesięcy w dni:

1 miesiąc = 30 dni

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilogramy

Bibliografia

1. Larson, r. 2012. Przedłużanie. 8. Wydanie. Cengage Learning.
2. Monterey Institute. Ocena funkcji. Odzyskane z: Montereyinstitute.org.
3. Stewart, J. 2007. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
4. Sullivan, m. 1997. Przedłużanie. 4. Wydanie. Edukacja Pearsona.
5. Zill, d. 2008. Prefrecment z postępami obliczeniowymi. 4. Wydanie. McGraw Hill.