Wypukłe lustro

Co to jest wypukłe lustro?

On wypukłe lustro Lub rozbieżne jest zakrzywione lustro, prawie zawsze sferycznie i z odblaskową powierzchnią po zewnętrznej stronie kuli, takiej jak ozdoby choinki. Dzięki wypukłym lusterkom jest to możliwe.

Na przykład lustra umieszczone na ulicach w celu ułatwienia tranzytu pojazdów na wąskich krzyżach są wypukłe, ponieważ wytwarzają obraz o szerokim polu widzenia.

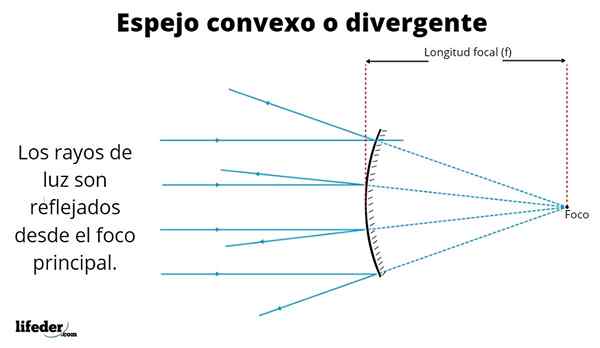
Ilustracja wypukłego lustra

Utworzone w ten sposób obrazy są zróżnicowane, w zależności od miejsca, w którym obiekt jest umieszczony. Najwyższy obraz pokazuje promienie równoległe z odległej fontanny, takiej jak słońce.

Promienie są odzwierciedlone zgodnie z prawem odbicia, które wskazuje, że kąt występowania błyskawicy jest taki sam. Jak widzimy, promienie odbijane są oddzielone - nie krzyżują się - kiedy opuszczają powierzchnię dystansową, dlatego tego rodzaju lustro jest również znane jako znane jako rozbieżny.

Kiedy odbicia odciągają się od lustra - nieciągłe linie na rysunku - przecinają się w punkcie zwanym ostrością.

Charakterystyka wypukłych luster

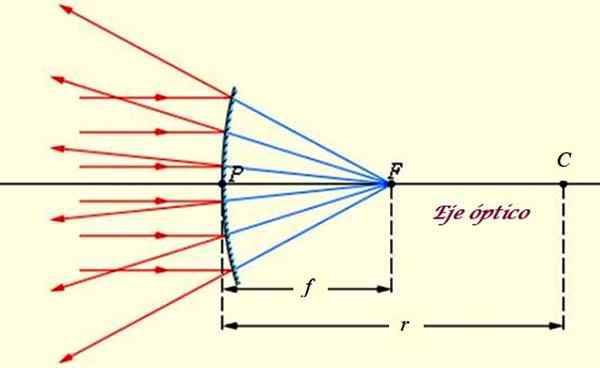Wypukłe lub rozbieżne lustro, na które wpływa promienie odległej fontanny, takie jak słońce. Źródło: f. Zapata.

Lustro wypukłe ma następujące cechy (patrz Superior Image):

-Godne uwagi punkty lustra to:

• C Środek, który zbiega się ze środkiem kuli, do której należy lustro.
• F Focus, gdzie zbieżą się promienie odbijane za lustrem.
• Wierzchołek p tego samego, który odpowiada środkowi sferycznej powierzchni i jest zdenerwowany z C i F.

Może ci służyć: ío (satelita)

-Ma Oś optyczna albo Głównej osi, która jest linią prostopadłą do powierzchni dystansowej. Promienie wpływające na oś optyczne znajdują odbite w tym samym kierunku.

-Środek kuli, do której należy lustro, znajduje się w punkcie C i R, jest jego promień. C jest znany jako Centrum krzywizny, chwila R czy on jest Promień krzywizny i wskazuje, jak zakrzywione jest lustro: nieletnie R, Bardziej podkreślona jest forma wypukła.

-Punkt przecięcia odbijanych promieni jest znany jako Punkt centralny lustra. Odległość między F i P jest w przybliżeniu R/2:

F = r/2

To wyrażenie jest ważne dla luster, których rozmiar jest znacznie niższy niż jego promień krzywizny.

-Obraz, który tworzy, jest mniejszy, a także wirtualny, ponieważ znajduje się za lustrem, jak zobaczymy.

Tworzenie obrazu w wypukłym lustrze

Wiedzieć, w jaki sposób obraz tworzony w lusterku wypukłym jest leczenie promienie.

Promienie te znajdują się odbijane na powierzchni lustra, a promienie odbijane są również rysowane. Metoda Ray ma zastosowanie do dowolnego lustra, a nie tylko wypukłych.

Przedłużając odbite promienie, przecinają się w pewnym momencie i właśnie tam powstaje obraz. Rozszerzenie odbijanych promieni pochodzących z rozszerzonego obiektu jako drzewa, jest pokazane na dolnej figurze przez nieciągłe linie.

Na dolnym rysunku rysowane są trzy promienie z obiektu, bardzo szczególne i łatwe do narysowania, a także jego odbicia:

Może ci służyć: rozszerzenie termiczne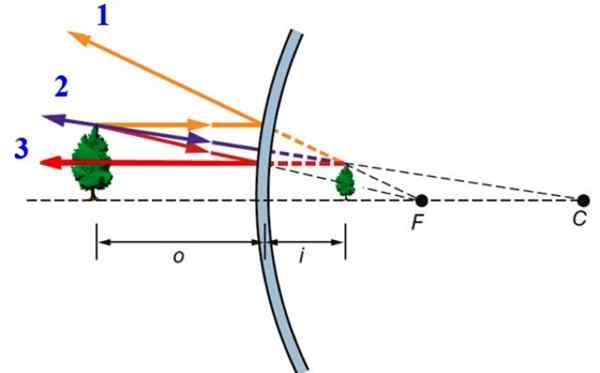 Rysunek 2.- Tworzenie obrazu w wypukłym lustrze. Źródło: f. Zapata.

-Ray 1, który wpływa równolegle do osi optycznej.

-Ray 2, który wpływa na egzolitację odbitego promienia, przechodzi dokładnie przez skupienie lustra, to znaczy punkt F. Ten promień jest odbity równolegle do osi optycznej.

-Wreszcie Ray 3, który dociera prostopadle do powierzchni sferycznej i z tego powodu znajduje się odbijane w tym samym kierunku.

Zasadniczo ta procedura dotyczy każdego punktu drzewa, ale w przypadku informacji uzyskanych z 3 rysowanych promieni wystarczy znaleźć obraz obiektu: jest uformowany za lustrem, jest właściwa i mniejsza niż oryginalna.

Przykłady i zastosowania wypukłych luster

Wiele bardzo pociągniętych sferycznych powierzchni działa jak wypukłe lustra, na przykład jasne i srebrne ozdoby świąteczne, a także nowe i jasne stalowe łyżki.

Na przykład wypukłe lustra mają wiele praktycznych zastosowań:

Zwierciadły zapobiegające wypadkom ruchu

Wypukłe lustra na ulicach i drogach pomagają uniknąć wypadków, ponieważ pozwalają zobaczyć ruch pochodzący z zakrętów.

Lustra nadzoru

W sklepach i bankach zwykle znajdują się wypukłe lustra do wykrywania złodziei, a także unikanie zderzeń między ludźmi i pojazdami wózków widłowych, które krążą w korytarzach i między półkami.

Lusterko wsteczne

Samochody i motocykle mają wypukłe lustra, które wytwarzają nieco mniejsze obrazy, ale obejmują więcej pola widzenia niż płaskie lustra.

Teleskop Cassegrain

Jedno z luster reflektora Cassegrain, wtórne lustro, jest wypukłe, chociaż nie jest sferyczne i służy do odbicia obrazu w kierunku głównego lustra teleskopu.

Może ci służyć: energia grawitacyjna: formuły, cechy, zastosowania, ćwiczenia

Wypukłe równania lustrzane

Rozważ prostokąty z poniższego rysunku, określone przez Ray 1, który pochodzi od górnej części strzałki, jego odbicie i przedłużenia tego.

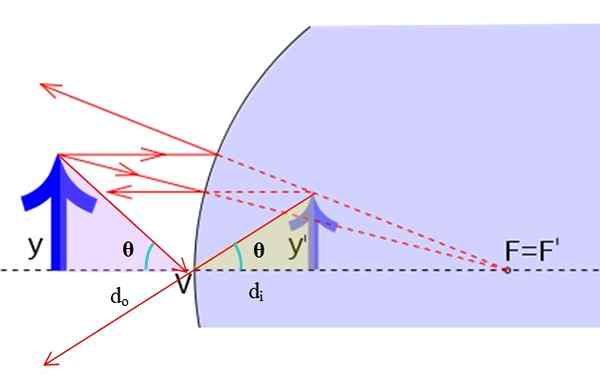Geometria do znalezienia powiększenia lustra. Źródło: f. Zapata.

Oryginalny obraz ma wysokość i podczas gdy wysokość wirtualnego obrazu jest i ' . To prawda, że:

Tan θ = y/d_albo = Y '/d_Siema

Powiększenie lustra

Przyczyną między wysokością obrazu a wysokością obiektu jest Powiększenie lustra, Nazywa się to, nawet jeśli uzyskany obraz jest mniejszy niż rzeczywisty obiekt. Oznaczamy to przez M:

M = y '/ y = d_Siema /D_albo

Związek między obiektem a jego obrazem w lusterku wypukłym

Rozważmy teraz tę drugą liczbę, w której region AVF można uznać za w przybliżeniu jako prawy trójkąt, ponieważ krzywizna lustra nie jest bardzo wyraźna. Dlatego:

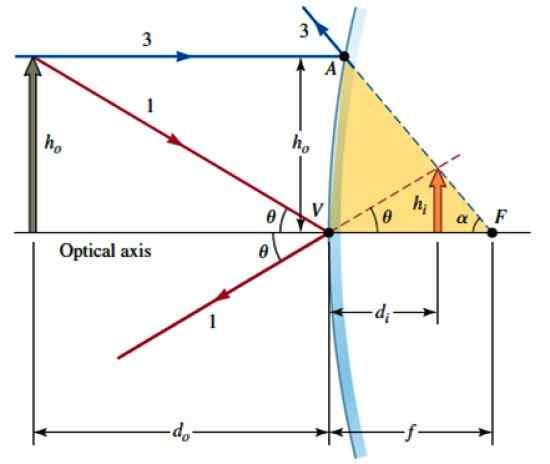Geometria do znalezienia matematycznej relacji między obiektem a jego obrazem. Źródło: Katz, D. Fizyka dla naukowców i inżynierów.

Av ≈ h_albo

Więc:

Tan α = h

Dlatego:

Odwrotność tego wyrażenia jest powiększenie:

Dlatego:

1- (d_Siema /f) = D_Siema /D_albo

Dzieląc wszystko między D_Siema:

Wreszcie:

 Teraz, w przypadku lustrzanych znaków, obowiązują konwencje. Rzeczywiście, chociaż wiemy, że odległość jest zawsze pozytywna, na wszystkich odległości za lustrem, wyróżniają się znakiem ujemnym.

Dlatego as F I D_Siema Są za lustrem, są mniej znane, a na odległość d_albo To nie jest konieczne, ponieważ wyprzedza lustro. Zatem poprzednie równanie pozostaje:

Można wykazać, że to równanie jest również ważne dla wklęsłego lustra.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Głośność 2. MC Graw Hill.
2. Giambattista, a. 2010. Fizyka. 2. Wyd. McGraw Hill.
3. Katz, d. 2017. Fizyka dla naukowców i inżynierów. Cengage Learning.
4. Thomas, w. 2008. Fizyka koncepcyjna. McGraw Hill.
5. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. McGraw Hill.