Wzór i równania wysiłek napięcia, obliczenia, ćwiczenia

On Odkształcenie naprężenia Jest zdefiniowany jako siła prostopadła do obszaru na jednostkę powierzchni zastosowaną do obiektu na jego końcach, aby ćwiczyć przyczepność. Jego wymiary są siły / obszaru i w formie matematycznej możemy to wyrazić w następujący sposób:

τ = f / a

Jedność wysiłków w międzynarodowym systemie jednostek jest taka sama, która jest wykorzystywana do presji: Pascal, skrót PA, co odpowiada 1 Newton/ M².

Rysunek 1. Jeśli wysiłek napięcia przekracza określoną wartość, lina jest zepsuta. Źródło: Pxhere.

W wysiłku napięcia istnieją dwie siły, które mają zastosowanie w tym samym kierunku i przeciwne zmysły, które rozciągają ciało. Jeśli pierwotnie długość obiektu wynosiła l_albo, Podczas stosowania wysiłku napięcia nowa długość wynosi l, a rozciąganie ΔL jest obliczane przez:

ΔL = L - L_albo

Solidne obiekty mają elastyczność w większym lub mniejszym stopniu, co oznacza, że ​​gdy wysiłek napięcia znika, wracają do swoich pierwotnych wymiarów.

Dzieje się tak, pod warunkiem, że wysiłek nie jest tak wielki, aby spowodować trwałe odkształcenie. Materiały gumowe, gumowe lub gumowe są dobre dla elastycznych przedmiotów, a także mają te wysokiej jakości włosy i skórę, między innymi.

[TOC]

Jednolite odkształcenie

Badając, w jaki sposób ciała są deformowane pod napięciem, bardzo wygodne jest zdefiniowanie koncepcji Jednolite odkształcenie, Ilość uwolniona. Jednolitalne odkształcenie jest oznaczone grecką literą δ (małe „delta”) i jest obliczane w następujący sposób:

δ = δL /L_albo

Jednostkowe odkształcenie służy do stosunkowo oceny deformacji obiektu w napięciu. Zobaczmy to w ten sposób: nie jest tak samo, aby rozciągnąć 1 cm pręt o długości 1 metra, aby rozciągnąć 1 cm na kolejne 10 m. W pierwszym przypadku deformacja jest znacznie bardziej znacząca niż w drugim.

Może ci służyć: Ohm: Mierniki oporowe, przykłady i ćwiczenia rozwiązane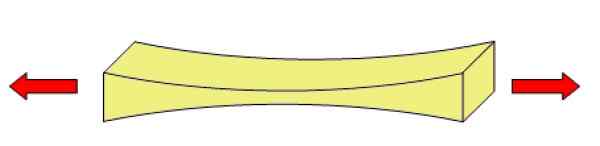Rysunek 2. Obiekt poddawany napięciu lub trakcji jest zdeformowany. Źródło: Wikimedia Commons.

Jak obliczany jest wysiłek napięcia? (Przykłady)

Angielski i współczesny fizyk Newtona o imieniu Robert Hooke (1635-1703), badał elastyczne właściwości ciał i ustanowiło prawo, które nosi jego imię. Wraz z tym wysiłek dotyczy odkształcenia, gdy wysiłek jest mały, jest powiązany:

Wysiłek ∝ Deformacja (Unital)

Logiczne jest oczekiwanie, że im większy wysiłek naprężenia, wystąpi większe wydłużenie. Korzystanie z określonych definicji:

τ ∝ δ

Stała proporcjonalności niezbędna do ustalenia równości jest oznaczona i jest znana jako moduł młodego lub elastyczności, charakterystyczny dla materiałów:

τ = y⋅δ

Moduł Younga ma takie same jednostki napięcia, ponieważ deformacja jednostkowa jest bezwymiarowa.

Tak więc sposób na obliczenie wysiłku naprężenia w ciele o właściwościach sprężystości jest mierzenie deformacji i znajomość jego młodego modułu. Ta ilość została określona eksperymentalnie dla wielu materiałów i jest tabelowana.

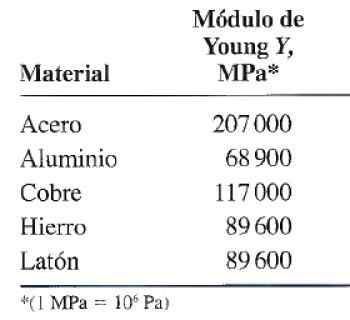Rysunek 3. Tabela elastyczności lub modułu Younga dla niektórych powszechnych materiałów użytkowania. Źródło: Valera Negrete, J. 2005. Ogólne uwagi fizyki. Unam.

Przykład obliczeń

Załóżmy, że stal o średnicy 3 mm jest poddawana wysiłku napięcia, zwisając z niej na wagę 250 N, jaka byłaby wielkość wspomnianego wysiłku?

Cóż, możemy wykorzystać definicję wysiłku napięcia jako iloraz między siłą prostopadłą do powierzchni a obszarem wspomnianej powierzchni. Najpierw obliczmy obszar, zakładając, że okrągły przewód krzyżowy:

Może ci służyć: numer masowy: co to jest i jak go zdobyć (z przykładami)

A = π . (D/2)² =  π . (D² /4)

Średnica drutu wynosi 3 mm i jednostki te muszą zostać przekształcone w metry:

D = 3 x 10^-3 M.

A = π . (3 x 10^-3 M)² / 4 = 7.07 x 10^-6 M².

Wysiłek napięcia jest wytwarzany przez ciężar zwisający z drutu, który jest stosowany prostopadle do jego przekroju, dlatego:

τ = 250 N / 7.07 x 10^-6 M² = 3.5 x 10 ⁷ Rocznie

Pascal jest dość małą jednostką, więc wielokrotności nie są niczym niezwykłym. Wiedząc, że 1 mega-pascal (MPA) to 10⁶ Pascal, wysiłek napięcia pozostaje:

τ = 35 MPa

Rozwiązane ćwiczenia

- Ćwiczenie 1

Moduł elastyczności pręta wynosi 4 x 10^jedenaście Rocznie. Jakie odkształcenie jednostkowe uzyskuje się poprzez zastosowanie wysiłku napięcia 420 MPa?

Rozwiązanie

Równanie, które należy zastosować, to:

τ = y⋅δ

Wraz z nim obliczamy jednolite odkształcenie:

δ = τ / y = 420 x 10⁶ PA/ 4 x 10^jedenaście PA = 0.00105

δ = δL /L_albo

Dlatego deformacja ΔL to:

ΔL = 0.00105 L_albo

Jeśli na przykład pręt miał pierwotnie o długości 1 metra, z tym wysiłkiem napięcia rozciąga się tylko 0.00105 M = 1.05 mm.

- Ćwiczenie 2

Drut stalowy ma 1.50 m długości i średnica 0.400 mm. Jeden z końców jest przymocowany do dachu, a masowy odbłyśnik jest umieszczany na drugim M = 1.50 kg, który został wydany. Oblicz:

a) odcinek drutu.

b) Jednolite odkształcenie i jednolity procent deformacji. Czy to możliwe, że drut jest zepsuty przez ciężar reflektora?

Rozwiązanie

Drut się rozciągnie, ponieważ odbłyśnik jest poddawany wysiłku napięcia. Siła wytwarzana przez ten wysiłek jest wagą odbłyśnika.

Może ci służyć: fizyka przed Greków (Antigua Grecja)

Waga obiektu masy jest iloczynem masy przez wartość przyspieszenia grawitacji, dlatego:

F = 1.50 kg x 9.8 m/s² = 14.7 n

Potrzebna jest krzyż sekcja drutu:

A =  π . (D² /4) = π x (0.4 x 10-3 m) 2/4 = 1.26 x 10^-7 M².

Z tymi wynikami obliczany jest wysiłek wywierany na drut:

τ = 14.7 n / 1.26 x 10^-7 M² = 1.17 x 10⁸ Rocznie

Drut ma elastyczne zachowanie, dlatego należy założyć, że prawo Hooke'a jest spełnione:

τ = y⋅δ

Z tabeli modułów elastyczności stwierdzamy, że dla stali y = 207 x 10⁹ Rocznie. Ponadto jednolite odkształcenie to:

δ = δL /L_albo

Zastąpienie w równaniu dla wysiłku:

τ = y⋅δ = y⋅ (δL /L_albo)

Dlatego rozciąganie to:

ΔL = L_albo τ / y =

= 1.50 m x 1.17 x 10⁸ PA / 207 x 10⁹ PA = 8.5 x 10^-4 M = 0.849 mm.

Jednolitym odkształcenie drutu wynosi:

δ = δL /L_albo = 8.5 x 10^-4 M / 1.5 m = 5.652 x 10^-4

Jeśli wyrażamy to jako procent, procentowe odkształcenie wynosi 0.0565 %, mniej niż 0.1 %, dlatego oczekuje się, że drut odporność na masę odbłyśnika bez zerwania, ponieważ odkształcenie, którego doświadcza, nie jest zbyt duże w porównaniu z pierwotną długością.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Piwo, f. 2010. Mechanika materiałów. McGraw Hill. 5. Wydanie.
3. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
5. Valera Negrete, J. 2005. Ogólne uwagi fizyki. Unam.