Standardowy błąd oszacowania Jak obliczone, przykłady, ćwiczenia

On Standardowy błąd szacowania Zmierzyć odchylenie w próbie wartości populacji. Oznacza to, że standardowy błąd oszacowania mierzy możliwe zmiany średniej próbki w odniesieniu do prawdziwej wartości średniej populacji.

Na przykład, jeśli chcesz poznać średni wiek populacji kraju (w średnim populacji), przyjmuje się niewielka grupa mieszkańców, którą nazwiemy „pokazami”. Z niego wyodrębnia się średni wiek (średnia próbki) i zakłada się, że populacja ma ten średni wiek z standardowym błędem szacunkowym, który różni się mniej więcej.

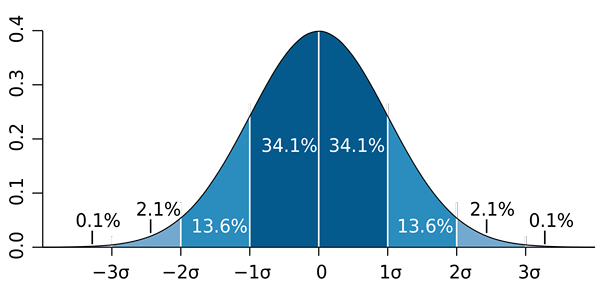
M. W. Toews [CC przez 2.5 (https: // creativeCommons.Org/licencje/według/2.5)]

Należy zauważyć, że ważne jest, aby nie mylić odchylenia standardowego ze standardowym błędem i błędem standardowym oszacowania:

1- Odchylenie standardowe jest miarą dyspersji danych; to znaczy jest miarą zmienności populacji.

2- Błąd standardowy jest miarą zmienności próbki, obliczonej na podstawie odchylenia standardowego populacji.

3- Standardowy błąd oszacowania jest miarą błędu popełnianego podczas przyjmowania średniej próbki jako oszacowania średniej populacji.

[TOC]

Jak to jest obliczane?

Błąd szacowania standardowego można obliczyć dla wszystkich miar uzyskanych w próbkach (na przykład standardowy średni błąd szacowania lub błąd standardowy oszacowania odchylenia standardowego) i mierzy błąd popełniany przy szacowaniu prawdziwej miary populacji z jej wartości próbki

Z standardowego błędu oszacowania budowany jest przedział ufności odpowiedniej miary.

Może Ci służyć: Matryca odwrotna: Obliczanie i ćwiczenie rozwiązane

Ogólna struktura wzoru dla standardowego błędu oszacowania jest następująca:

Błąd standardowego oszacowania = ± współczynnik zaufania * Błąd standardowy

Współczynnik zaufania = wartość graniczna przykładowej statystyki lub rozkładu próbkowania (między innymi Normal lub Gauss Bell, Student T) dla pewnego przedziału prawdopodobieństwa.

Błąd standardowy = odchylenie standardowe populacji podzielone przez pierwiastek kwadratowy wielkości próby.

Współczynnik ufności wskazuje ilość standardowych błędów, które są gotowe dodać i odejmować dostosowane do pewnego poziomu zaufania do wyników.

Przykłady obliczeń

Załóżmy, że próbujesz oszacować odsetek ludzi w populacji, którzy mają zachowanie a, i chcesz mieć 95% zaufania do swoich wyników.

Próbka n osób jest pobierana, a odsetek próbki P i jej dopełniacza Q.

Błąd standardowego oszacowania (EEE) = ± Współczynnik zaufania * Błąd standardowy

Współczynnik zaufania = Z = 1.96.

Błąd standardowy = pierwiastek kwadratowy przyczyny między iloczynem proporcji próbki dla jej dopełniacza a wielkością próbki n.

Na podstawie standardowego błędu oszacowania odstęp, w którym powstaje odsetek populacji lub odsetek innych próbek, które można utworzyć z tej populacji, przy 95% poziomu ufności:

P -eee ≤ proporcja populacji ≤ P + EEE

Rozwiązane ćwiczenia

Ćwiczenie 1

1- Załóżmy, że próbujesz oszacować odsetek osób w populacji, które preferują wzbogaconą formułę mleczarską, i chcesz mieć 95% zaufania do swoich wyników.

Może ci służyć: podział syntetyczny

Próbka 800 osób jest podejmowana i ustalono, że 560 osób w próbce preferuje wzbogaconą formułę mleczarską. Określić interwał, w którym można oczekiwać proporcji populacji, oraz odsetek innych próbek, które można pobrać z populacji, z 95% zaufaniem

a) Obliczmy proporcję próbki P i jej uzupełnienie:

P = 560/800 = 0.70

Q = 1 -p = 1-0.70 = 0.30

b) Wiadomo, że proporcja zbliża się do rozkładu normalnego do próbek dużych rozmiarów (większy niż 30). Następnie stosuje się regułę 68 - 95 - 95.7 i musisz:

Współczynnik zaufania = Z = 1.96

Błąd standardowy = √ (p*q/n)

Standardowy błąd oszacowania (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Na podstawie standardowego błędu oszacowania ustalono interwał, w którym oczekuje się proporcji populacji przy 95% poziomu ufności:

0.70 -0.0318 ≤ proporcja populacji ≤ 0.70 + 0.0318

0.6682 ≤ proporcja populacji ≤ 0.7318

Możesz oczekiwać, że 70% proporcji próbki zmieni się do 3.18 punktów procentowych, jeśli zajmuje inną próbkę 800 osób lub że rzeczywisty odsetek populacji wynosi od 70 do 3.18 = 66.82% i 70 + 3.18 = 73.18%.

Ćwiczenie 2

2- Weźmiemy z Spiegel i Stephens, 2008, następujące studium przypadku:

Spośród całkowitych klas matematyki pierwszych studentów uniwersytetu pobrano losową próbkę 50 kwalifikacji, w której znaleziona średnia wyniosła 75 punktów, a odchylenie standardowe, 10 punktów. Jakie są 95% limity ufności dla oceny średniej kwalifikacji matematyki uniwersytetu?

Może ci służyć: jaki jest związek między obszarem Rhombusa a prostokątem?

a) Obliczmy standardowy błąd oszacowania:

95%współczynnik ufności = z = 1.96

Błąd standardowy = s/√n

Standardowy błąd oszacowania (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Z standardowego błędu oszacowania, przedziału, w którym powstaje średnia populacji lub średnia innej próby 50, przy 95% poziomu ufności:

50 -2.7718 ≤ średniej populacji ≤ 50 + 2.7718

47.2282 ≤ średniej populacji ≤ 52.7718

c) Możesz oczekiwać, że średnia próbki zmieni się do 2.7718 punktów, jeśli pobrana jest inna próbka 50 klas lub że realna średnia z klas matematycznych populacji uniwersytetu wynosi od 47.2282 punktów i 52.7718 punktów.

Bibliografia

1. Abraira, v. (2002). Odchylenie standardowe i błąd standardowy. Magazyn Semergen. Web odzyskał.Archiwum.org.
2. Rumsey, d. (2007). Pośrednie statystyki dla manekinów. Wiley Publishing, Inc.
3. Salinas, godz. (2010). Statystyki i prawdopodobieństwa. Wyzdrowiał z mat.Uda.Cl.
4. SAKAL, r.; Rohlf, f. (2000). Biometria. Zasady i praktyka statystyki w badaniach biologicznych. Trzeci wyd. Blume Editions.
5. Spiegel, m.; Stephens, L. (2008). Statystyka. Czwarty ed. McGraw-Hill/Inter-American z Meksyku S. DO.
6. Wikipedia. (2019). 68-95-99.7 Zasada. Odzyskane z.Wikipedia.org.
7. Wikipedia. (2019). Standardowy błąd. Odzyskane z.Wikipedia.org.