Mechaniczne wzory energii, koncepcja, typy, przykłady, ćwiczenia

energia mechaniczna obiektu lub systemu jest definiowane jako suma jego energii potencjalnej i energii kinetycznej. Jak sama nazwa wskazuje, system nabywa energię mechaniczną dzięki działaniu sił mechanicznych, takich jak waga i siła elastyczna.

Zgodnie z ilością energii mechanicznej, jaką ma ciało, będzie ono również miało możliwość wykonywania pracy mechanicznej.

Rysunek 1. Ruch Roller Mountain Car można opisać przez zachowanie energii mechanicznej. Źródło: Pixabay.

Energia - typ, który jest - jest ilością skalarną, a zatem brakuje kierunku i znaczenia. Być I_M Energia mechaniczna obiektu, LUB jego potencjalna energia i K Jego energia kinetyczna, formuła do jej obliczenia, jest:

I_M = K + u

Jednostką w jakimkolwiek międzynarodowym systemie energetycznym jest Joule, który jest skrócony jako J. 1 J jest równoważne 1 N.M (Newton na metr).

Jeśli chodzi o energię kinetyczną, oblicza się w następujący sposób:

K = ½ m.v²

Gdzie M Jest to masa obiektu i v Jego prędkość. Energia kinetyczna jest zawsze dodatnią ilością, ponieważ masa i kwadrat prędkości są. Jeśli chodzi o energię potencjalną, jeśli chodzi o grawitacyjną energię potencjalną, masz:

U = m.G.H

Tutaj M To wciąż jest ciasto, G Jest to przyspieszenie grawitacji i H Jest to wysokość w stosunku do poziomu odniesienia lub jeśli jest preferowana, podłoże.

Teraz, jeśli omawiane ciało ma elastyczną energię potencjalną -może to być sprężyna -to dlatego, że jest skompresowana lub może wydłużona. W takim przypadku powiązana energia potencjalna to:

U = ½ kx²

Z k jako stała sprężyna, która wskazuje, jak łatwa lub trudna jest ją zdeformowana i X Długość wspomnianego deformacji.

[TOC]

Koncepcja i cechy energii mechanicznej

Pogłębienie podanej wcześniej definicji, energia mechaniczna zależy następnie od energii związanej z ruchem ciała: energia kinetyczna, a także wkład energii potencjalnej, co, jak powiedzieliśmy, może być grawitacyjne, zarówno ze względu na wagę, jak i wagę i pozycję zajmującą organizm szacunek dla poziomu gleby lub odniesienia.

Zilustrujmy to prostym przykładem: załóżmy, że masz garnek na podłodze i na spoczynku. Ponieważ nadal nie ma energii kinetycznej, a także na ziemi, miejsce, w którym nie może upaść; Dlatego brakuje mu grawitacyjnej energii potencjalnej, a jej energia mechaniczna wynosi 0.

Załóżmy, że teraz ktoś umieszcza garnek na krawędzi dachu lub okna, o 3.0 metrów wysokości. W tym celu osoba musiała wykonywać pracę przeciwko grawitacji. Garnek ma teraz grawitacyjną energię potencjalną, może spaść z tej wysokości, a jej energia mechaniczna nie jest już nieważna.

Rysunek 2. Garnek na oknie ma grawitacyjną energię potencjalną. Źródło: Pixabay.

W tych okolicznościach ma garnek I_M = U I ta ilość zależy od wysokości i masy doniczki, jak wskazano wcześniej.

Powiedzmy, że garnek pada, ponieważ był w niepewnej pozycji. Wraz ze wzrostem prędkości i wraz z nią energia kinetyczna, podczas gdy grawitacyjna energia potencjalna maleje, ponieważ traci wysokość. Energia mechaniczna w dowolnym momencie upadku to:

Może ci służyć: jakie są pochodne wielkości?

I_M = U + k = ½ m.v² + M.G.H  

Siły konserwatywne i niekonserwatywne

Kiedy garnek jest na pewnej wysokości, ma grawitacyjną energię potencjalną, ponieważ wspinał się na nią, wykonał pracę przeciwko grawitacji. Wielkość tej pracy jest warta takiej samej jak ten, który robi grawitację, gdy garnek spada Z tej samej wysokości, ale ma przeciwny znak, ponieważ został wykonany przeciwko niemu.

Praca, która wymusza, takie jak grawitacja i elastyczność, zależy tylko od pozycji początkowej i pozycji końcowej uzyskanej przez obiekt. Bez względu na trajektorię nastąpiła od jednego do drugiego, tylko same wartości mają znaczenie. Siły, które zachowują się w ten sposób, są nazywane Siły konserwatywne.

A ponieważ są konserwatywni, pozwalają, aby praca wykonana przez nich była przechowywana jako energia potencjalna w konfiguracji obiektu lub systemu. Dlatego garnek na krawędzi okna lub dachu miał możliwość upadku, a wraz z nim rozwinąć ruch.

Z drugiej strony istnieją siły, których prace zależą od ścieżki, a następnie obiektu, na którym działają. Tarcie należy do tego rodzaju sił. Podeszwy butów będą wydawane więcej, gdy przejdziesz z jednego miejsca na drugie na drodze z wieloma okrążeniami, niż kiedy wybierzesz kolejne bezpośrednio.

Siły tarcia wykonują pracę, która zmniejsza energię kinetyczną ciał, ponieważ je spowalnia. I dlatego energia mechaniczna systemów, w których działa tarcie.

Na przykład część pracy wykonanej przez siłę jest tracona przez ciepło lub dźwięk.

Rodzaje energii mechanicznej

Energia mechaniczna jest, jak powiedzieliśmy, suma energii kinetycznej i energii potencjalnej. Teraz energia potencjalna może pochodzić z różnych sił konserwatywnych: waga, wytrzymałość sprężystość i siła elektrostatyczna.

- Energia kinetyczna

Energia kinetyczna to skalarna ilość, która zawsze staje się ruchem. Każda cząstka lub ruchomy obiekt ma energię kinetyczną. Obiekt, który porusza się w linii prostej, ma energię kinetyczną tłumaczenia. To samo dzieje się, jeśli się obraca, w tym przypadku mówi się o obrotowej energii kinetycznej.

Na przykład samochód, który porusza się wzdłuż drogi, ma energię kinetyczną. Także piłka nożna podczas poruszania się po boisku lub osoby, która pospiesznie idzie, aby dotrzeć do biura.

- Energia potencjalna

Zawsze można powiązać funkcję skalarną zwaną energią potencjalną z siłą konserwatywną. Wyróżnia się następujące:

Grawitacyjna energia potencjalna

Ten, który wszystkie obiekty mają na mocy swojej wysokości w odniesieniu do ziemi lub poziomu odniesienia, który został wybrany jako taki. Jako przykład, ktoś, kto spoczywa na tarasie 10 -story budynku, ma energię potencjalną 0 w odniesieniu do gruntu tarasu, ale nie w odniesieniu do ulicy, która znajduje się 10 pięter poniżej.

Elastyczna Energia potencjalna

Zazwyczaj jest przechowywany w obiektach takich jak ligi i źródła, związane z odkształceniem, jakie doświadczają podczas ich rozciągania lub kompresji.

Elektrostatyczna energia potencjalna

Jest przechowywany w systemie obciążeń energii elektrycznej w równowadze, ze względu na interakcję elektrostatyczną między nimi. Załóżmy, że istnieją dwa ładunki elektryczne tego samego oddzielnego znaku w niewielkiej odległości; Ponieważ opłaty elektryczne o tym samym znaku są odpychane, oczekuje się, że agent zewnętrzny wykonał pracę, aby zbliżyć.

Może ci służyć: Obwody bieżące naprzemienne: typy, aplikacje, przykłady

Po ustawieniu systemu udaje się przechowywać pracę, którą agent wykonał, aby je skonfigurować, w postaci elektrostatycznej energii potencjalnej.

Ochrona energii mechanicznej

Wracając do spadającego garnka, grawitacyjna energia potencjalna, jaką miała, gdy była na krawędzi dachu, jest przekształcana w kinetyczny ruch ruchu. Wzrasta to kosztem pierwszego, ale suma obu pozostaje stała, ponieważ upadek doniczki jest aktywowany przez grawitację, która jest siłą konserwatywną.

Istnieje wymiana między jednym rodzajem energii a drugą, ale pierwotna kwota jest taka sama. Dlatego ważne jest, aby potwierdzić, że:

Początkowa energia mechaniczna = końcowa energia mechaniczna

I_{Początkowe m} = E_{M Final}

Alternatywnie:

K_wstępny + LUB_wstępny = K _finał + LUB_finał

Innymi słowy, energia mechaniczna się nie zmienia i ∆E_M = 0. Symbol „∆” oznacza zmianę lub różnicę między końcową i początkową.

Aby poprawnie zastosować zasadę zachowania energii mechanicznej do rozwiązywania problemów, konieczne jest:

-Dotyczy to tylko wtedy, gdy siły działające w systemie są konserwatywne (nasilenie, sprężyste i elektrostatyczne). W tym wypadku: ∆E_M = 0.

-System badań musi być izolowany. W żaden sposób nie ma transferu energii.

-Jeśli pojawia się w problemach, to jest to, że jest to miękkie, to ∆E_M ≠ 0. Mimo to problem można rozwiązać poprzez znalezienie pracy wykonanej przez siły konserwatywne, ponieważ jest to przyczyna spadku energii mechanicznej.

Odliczenie mechanicznej ochrony energii

Załóżmy, że siła konserwatywna działa na system, który wykonuje pracę W. Ta praca powoduje zmianę energii kinetycznej:

W = ∆k (Twierdzenie o energii roboczej kinowej)

Należy zauważyć, że kinetyka twierdzenia o energii pracy ma zastosowanie nawet w przypadku sił niekonserwatywnych.

Z drugiej strony praca jest również odpowiedzialna za zmianę energii potencjalnej, aw przypadku siły konserwatywnej zmiana energii potencjalnej definiuje się jako negatywne tej pracy:

W = -∆u

Dopasowanie tych równań, ponieważ oba odnoszą się do pracy wykonanej w obiekcie:

∆K = -∆U 

K_F - K_albo = -(U_F - LUB_albo)

Klodowce symbolizują „finał” i „inicjał”. Grupowanie:

K_F + LUB_F = K_albo + LUB_albo                                                    

Przykłady energii mechanicznej

Wiele obiektów ma złożone ruchy, w których skomplikowane jest znalezienie wyrażeń dla pozycji, prędkości i przyspieszenia w funkcji czasu. W takich przypadkach zastosowanie zasady ochrony energii mechanicznej jest bardziej skuteczną procedurą niż próba bezpośredniego zastosowania przepisów Newtona.

Spójrzmy na niektóre przykłady, w których zachowuje się energię mechaniczną:

-Narciarz, który zjeżdża z dół po zaśnieżonych wzgórzach, pod warunkiem, że brak tarcia jest przypuszczalnie. W takim przypadku waga jest siłą sprawną ruchu w trakcie trajektorii.

-Rosyjskie wózki górskie, Jest to jeden z najbardziej typowych przykładów. Tutaj także waga jest siłą definiującą ruch i energię mechaniczną jest zachowana, jeśli nie ma tarcia.

Może ci służyć: energia jonizacyjna

-Proste wahadło Składa się z masy podlegającej niewydajnej linii -nie zmienia długości -która krótko oddziela się od pionowego i może oscylować. Wiemy, że ostatecznie się zatrzyma z powodu tarcia, ale gdy tarcie nie jest brane pod uwagę, energia mechaniczna jest również zachowana.

-Blok, który wpływa na wiosnę Naprawiono jeden koniec do ściany, wszystkie umieszczone na bardzo gładkim stole. Blok ściska sprężynę, przesuwa się w pewną odległość, a następnie zostaje wystrzelony w przeciwnym kierunku, ponieważ sprężyna się rozciąga. Tutaj blok nabywa swoją potencjalną energię dzięki pracy, która sprawia, że ​​wiosna.

-Wiosna i piłka: Kiedy sprężyna jest ściśnięta przez piłkę, to odbijanie. Dzieje się tak, ponieważ po zwolnieniu sprężyny energia potencjalna staje się energią kinetyczną w piłce.

-Skok trampoliny: Działa podobnie do wiosny, elastycznie promując osobę, która na niego skaczy. To wykorzystuje swoją wagę podczas skakania, z którymi deformuje trampolinę, ale ten, po powrocie do pierwotnej pozycji, daje impuls do zworki.

Rysunek 3. Ścieżka działa jak wiosna, promując ludzi, którzy na nią skaczą. Źródło: Pixabay.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Obiekt masy M = 1 kg jest upuszczany przez rampę z wysokości 1 m. Jeśli rampa jest wyjątkowo gładka, oblicz prędkość ciała, gdy koliduje sprężyna.

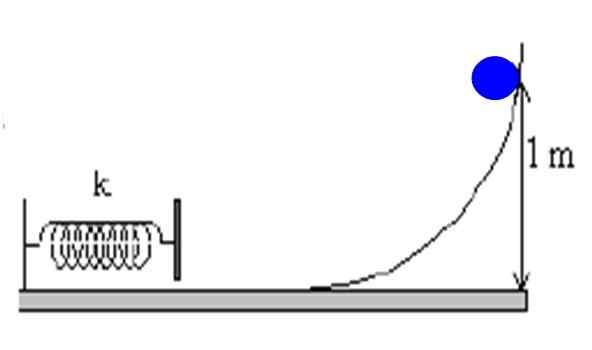Rysunek 4. Obiekt schodzi na rampie bez tarcia i ściska sprężynę przymocowaną do ściany. Źródło: f. Zapata.

Rozwiązanie

Oświadczenie informuje, że rampa jest gładka, co oznacza, że ​​jedyną siłą, która działa na ciało, jest jego waga, siła konserwatywna. Zatem wskazane jest zastosowanie ochrony energii mechanicznej między dowolnymi punktami trajektorii.

Rozważ punkty oznaczone na rycinie 5: A, B i C.

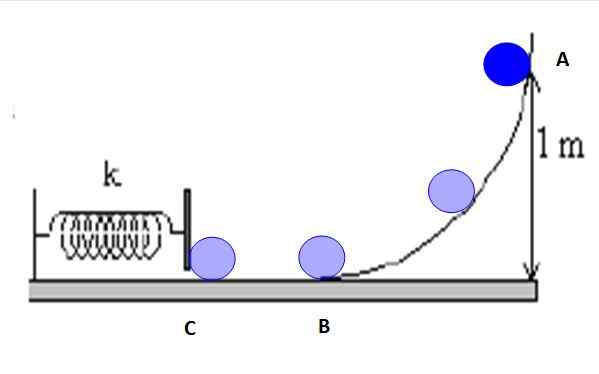Rysunek 5. Ścieżką podążającą za obiektem jest tarcie, a energia mechaniczna jest zachowana między dowolną parą punktów. Źródło: f. Zapata.

Możliwe jest ustanowienie ochrony energii między A i B, B i C lub A i C lub którykolwiek z punktów pośrednich na rampie. Na przykład, między A i C masz:

Energia mechaniczna w A = energia mechaniczna w C

I_mama = E_MC

K_DO + LUB_DO = K_C + LUB_C

½ m.v_DO² + M.G.H_DO = ½ m V_C² + M.G.H_C

Jak uwolnie się od punktu A, prędkość v_DO = 0, z drugiej strony H_C = 0. Ponadto masa jest anulowana, ponieważ jest to wspólny czynnik. Więc:

G.H_DO = ½ v_C²

v_C²= 2 g.H_DO

- Ćwiczenie 2

Znajdź maksymalną kompresję, jaką doświadczy sprężyna rozwiązywanego ćwiczenia 1, jeśli stała sprężystej tego samego wynosi 200 N/M.

Rozwiązanie

Stała sprężystości sprężyny wskazuje siłę, która ma być przyłożona w celu odkształcenia jednostki długości. Ponieważ stała tej wiosny jest warta k = 200 N/m, oznacza to, że 200 n jest wymagane do kompresji lub rozciągnięcia 1 m.

Być X Odległość, którą obiekt ściska sprężynę przed zatrzymaniem w punkcie D:

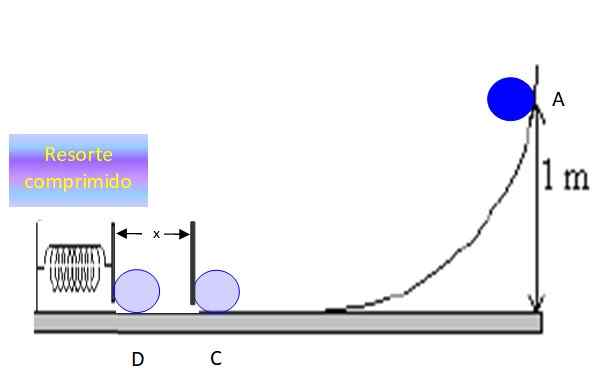Rysunek 6. Obiekt ściska sprężynę i odległość x i na chwilę zatrzymuje się. Źródło: f. Zapata.

Ochrona energii między punktami C i D stwierdza, że:

K_C + LUB_C = K_D + LUB_D

W punkcie C nie ma grawitacyjnej energii potencjalnej, ponieważ jej wysokość wynosi 0, ale ma energię kinetyczną. W D zatrzymał się całkowicie, dlatego tam_D = 0, ale zamiast tego masz do dyspozycji energia potencjalna sprężonej sprężyny u_D.

Ochrona energii mechanicznej pozostaje:

K_C = U_D

½ mV_C² = ½ kx²

 

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
3. Knight, r.  2017. Fizyka dla naukowców i inżynierii: podejście strategiczne. osoba.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
5. Wikipedia. Energia mechaniczna.Odzyskane z: jest.Wikipedia.org.