Gibbs Free Energy jednostki, sposób obliczania, rozwiązane ćwiczenia

Bezpłatna energia Gibbs (powszechnie nazywane g) jest potencjałem termodynamicznym zdefiniowanym jako różnica w entalpii H, z wyjątkiem iloczynu temperatury t, przez entropię systemu:

G = h - t s

Gibbs Free Energy jest mierzona w dżuli (według systemu międzynarodowego) w ERGIOS (dla systemu ligowego jednostek), w kalorii lub woltach elektronów (Dla elektro woltów).

Rysunek 1. Schemat pokazujący definicję energii Gibbs i jej związek z innymi potencjałami termodynamicznymi. Źródło: energia jądra.internet.

W procesach występujących przy stałym ciśnieniu i temperaturze zmienność energii swobodnej Gibbs wynosi δG = δH - t δs. W takich procesach (g) reprezentuje energię dostępną w systemie, która może stać się pracą.

Na przykład w egzotermicznych reakcjach chemicznych entalpia zmniejsza się, podczas gdy entropia rośnie. W funkcji GIBBS te dwa czynniki są przeciwdziałane, ale tylko wtedy, gdy energia Gibbsa zmniejsza reakcję.

Jeśli więc zmienność G jest ujemna, proces jest spontaniczny. Gdy funkcja GIBBS osiągnie minimum, układ osiąga stabilną równowagę. Krótko mówiąc, w procesie, dla którego ciśnienie i temperatura pozostają stałe, możemy potwierdzić:

- Jeśli proces jest spontaniczny, to ΔG < 0

- Gdy system jest w równowadze: ΔG = 0

- W procesie niestabilnym wzrasta: ΔG> 0.

[TOC]

Jak to jest obliczane?

Gibbs Free Energy (G) jest obliczany na podstawie definicji podanej na początku:

G = H - THSS

Z kolei entalpia H jest potencjałem termodynamicznym zdefiniowanym jako:

H = u + p v

- Krok po kroku

Następnie zostanie przeprowadzona analiza kroku -step, aby poznać niezależne zmienne, które energię Gibbs jest funkcją:

1- Z pierwszego prawa termodynamiki energia wewnętrzna jest związana z entropią systemu i jego objętością V dla odwracalnych procesów poprzez relację zróżnicowaną:

Może ci służyć: etydium bromek: struktura, właściwości, zastosowania, toksyczność

du = dq - dw = tds - PDV

Z tego równania wynika, że ​​energia wewnętrzna u jest funkcją zmiennych S i V:

U = u (s, v)

2- Począwszy od definicji H i przyjmuje różnicę:

DH = du + d (p v) = du + vdp + pdv

3- Zastąpienie wyrażenia DU uzyskanego w (1) musisz:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Stąd stąd stwierdza się, że entalpia H zależy od entropii i ciśnienia P, to znaczy:

H = H (S, P)

4- Obecnie obliczane jest całkowita różnica energii swobodnej Gibbs Uzyskiwanie:

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Gdzie DH został zastąpiony wyrażeniem znalezionym w (3).

5- Wreszcie, upraszczając, dostajesz: DG = VDP - SDT, Oczywiste jest, że energia swobodna g zależy od ciśnienia i temperatury t jako:

G = g (p, t)

- Relacje termodynamiczne Maxwella

Z analizy w poprzedniej sekcji wynika, że ​​energia wewnętrzna systemu jest funkcją entropii i objętości:

U = u (s, v)

Następnie różnica LUB Być:

du = ∂_SU |_V DS + ∂_VU |_S DV = TDS - PDV

Na podstawie tego wyrażenia w częściowych pochodnych można wywnioskować relacje termodynamiczne Maxwell Maxwell. Pochodne częściowe obowiązują, gdy funkcja zależy od więcej niż jednej zmiennej i można je łatwo obliczyć, stosując twierdzenie z poniższej sekcji.

Pierwszy związek Maxwella

 ∂_VT |_S = -Mon_SP |_V 

Aby dotrzeć do tego związku, Twierdzenie Clairaut - Schwarz na częściowych pochodnych, które stwierdzają:

„Mieszane pochodne drugiego rzędu ze zmiennymi wymienionymi są takie same, pod warunkiem, że funkcje, które mają być wyprowadzone, są ciągłe i różniczne”.

Drugi związek Maxwella

Począwszy od tego, co zostało wykazane w 3 punkcie poprzedniej sekcji:

Może ci służyć: czynniki wpływające na rozpuszczalność

H = H (S, P) i DH = TDS + VDP

Można uzyskać:

 ∂_PT |_S = ∂_SV |_P 

Postępuj w podobny sposób z wolną energią Gibbs G = g (p, t) i z swobodną energią Helmholtza F = f (t, v) Aby uzyskać pozostałe dwa termodynamiczne relacje Maxwella. 

Rysunek 2. Josiah Gibbs (1839–1903) był amerykańskim fizykiem, chemikiem i matematykiem, który wniósł wielki wkład w termodynamikę. Źródło: Wikimedia Commons.

Cztery relacje termodynamiczne Maxwella 

1- Powiązane z energią wewnętrzną u: ∂_VT |_S = -Mon_SP |_V

2- Ten uzyskany z entalpii h: ∂_PT |_S = ∂_SV |_P 

3- związane z energią Helmholtza f: ∂_TP |_V = ∂_VS |_T 

4- Połączone z energią swobodną Gibbsa G: ∂_TV |_P = -Mon_PS |_T

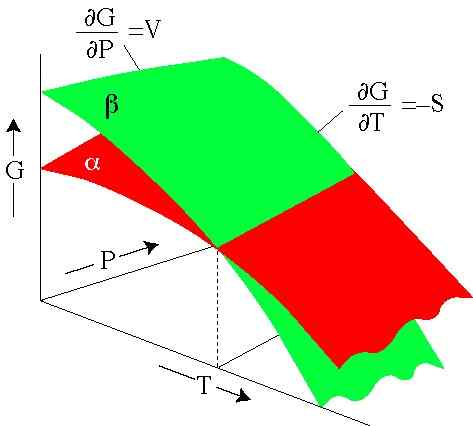Rysunek 2. Energia Gibbsa zależy od ciśnienia i temperatury. Każda powierzchnia reprezentuje fazę. (SERC.Carleton.Edu)

Rozwiązane ćwiczenia

Ćwiczenie 1

Oblicz zmianę energii swobodnej GIBBS dla 2 moli idealnego gazu w temperaturze 300k podczas rozszerzenia izotermicznego, co prowadzi do początkowego systemu objętości 20 litrów do końcowej objętości 40 litrów.

Rozwiązanie

Pamiętając o definicji swobodnej energii Gibbsa:

G = h - t s

Wówczas skończona odmiana F będzie:

ΔG = ΔH - t δs, Ponieważ δT = 0

W gazach idealnych entalpia zależy tylko od jej temperatury bezwzględnej, ale ponieważ jest to proces izotermiczny, a następnie δH = 0 i ΔG = - t δs.

W przypadku gazów idealnych odmiana entropii procesu izotermicznego wynosi: 

ΔS = nr ln (v₂/V₁)

To dotyczyło tego ćwiczenia:

ΔS = 2 mole x 8314 J/(k mol) x ln (40l/20l) = 11,53 J/k

Następnie możemy uzyskać zmianę energii Helmholtza:

ΔG = - 300K x 11,53 J/k = -3457,70 j.

Ćwiczenie 2

Biorąc pod uwagę, że energia swobodna GIBBS jest funkcją temperatury i ciśnienia g = g (t, p); Określić zmienność g podczas procesu, w którym temperatura się nie zmienia (izotermiczna) dla n moli idealnego gazu monoatomicznego.

Może ci służyć: wodorotlenek strontu (SR (OH) ₂)

Rozwiązanie

Jak pokazano powyżej, zmiana energii Gibbsa zależy tylko od zmiany temperatury T i objętości V, więc jego nieskończenie małe zmienność jest obliczana zgodnie z:

Dg = -sdt + vdp

Ale jeśli jest to proces, w którym temperatura jest stała, wówczas df = + vdp, więc skończona zmienność ciśnienia δp prowadzi do zmiany energii gibbsa podanej przez:

ΔG = + ∫ Vdp = + ∫ (n r t) dp/p = + n r t ln (δp)

Korzystanie z równania gazu idealnego:

P v = n r t

Podczas procesu izotermicznego zdarza się, że:

D (p v) = p dv + v dp = 0

To jest:

dp/p = - dv/v

Więc poprzedni wynik można zapisać w zależności od zmienności objętościowej Δv:

ΔG = + ∫ Vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (δv)

Ćwiczenie 3

Biorąc pod uwagę następującą reakcję chemiczną:

N₂0 (g) + (3/2) lub₂ (g) ↔️₂ (g) W temperaturze t = 298 K

Znajdź zmianę energii swobodnej Gibbs i poprzez uzyskany wynik, wskazuj, czy jest to proces spontaniczny.

Rozwiązanie

Poniżej kroków:

- Pierwszy krok: entalpie reakcji

ΔHr = 2*δh (nie₂ (g)) - ΔH (n₂0 (g)) = 2*33,2-81,6 = -15,2 kJ/mol

- Drugi krok: zmienność entropii reakcji

ΔSR = 2*s (nie₂ (g)) - s (n₂0 (g)) - (3/2) s (lub₂ (g)) = 2*240,1 - 220,1 - 1,5*205,2 = -47,7 j/(mol*k).

- Trzeci krok: Zmienność funkcji GIBBS

Ta wartość określi równowagę między zmniejszającą energią a rosnącą entropią, aby wiedzieć, czy reakcja jest wreszcie spontaniczna, czy nie.

ΔGR = ΔHr -t δSr = -15,2 -298*(-47,7) = -985,4 J/mol

Ponieważ jest to ujemna zmiana energii Gibbs, można stwierdzić, że jest to spontaniczna reakcja w temperaturze 298 k = 25 ºC.

Bibliografia

1. Castaños e. Ćwiczenia energetyczne. Odzyskane z: lidiaconlachimica.WordPress.com.
2. Cengel i. 2012. Termodynamika. 7. edycja. McGraw Hill.
3. Librettexts. Bezpłatna energia Gibbs. Odzyskane z: chem.Librettexts.org
4. Librettexts. Co to jest bezpłatna energia. Odzyskane z: chem.Librettexts.org
5. Wikipedia. Bezpłatna energia Gibbs. Odzyskane z: jest.Wikipedia.com
6. Wikipedia. Bezpłatna energia Gibbs. Źródło: w:.Wikipedia.com