ENEGON WŁAŚCIWE, JAK ZROBIĆ ENEGON, Przykłady

A ENEGON Jest to wielokąta dziewięciu stron i dziewięć wierzchołków, które mogą być regularne lub nie. Nominacja Enegona pochodzi od greckiego i składa się z greckich słów Ennea (Dziewięć i Gonon (kąt).

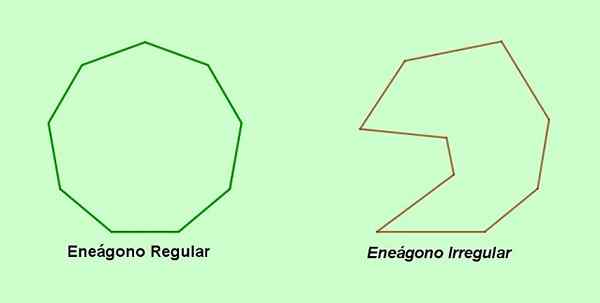
Alternatywną nazwą dla dziewięciokrotnego wielokąta jest słowo nie -słowo, które pochodzi z łaciny Nonus (Dziewięć i Gonon (wierzchołek). Z drugiej strony, jeśli boki lub kąty Eneregonu są dla siebie nierówne, jest wtedy Nieregularny ENEGON. Jeśli wręcz przeciwnie, dziewięć stron i dziewięć kątów Eneregonu jest równe, to jest to Regularny ENEGON.

Rysunek 1. Regularny Enegon i nieregularny ENEGON. (Własne opracowanie)

[TOC]

ENEGON WŁAŚCIWOŚCI

Dla wielokąta n boków suma jego wewnętrznych kątów wynosi:

(N - 2) * 180º

W ENEGON byłoby to n = 9, więc suma jego wewnętrznych kątów to:

SA = (9 - 2) * 180º = 7 * 180º = 1260º

W każdym wielokąta liczba przekątnej wynosi:

D = n (n - 3) / 2, aw przypadku Enegona, ponieważ n = 9, musisz d = 27.

Regularny ENEGON

W Enegon lub zwykłym nonagon.

Następnie konieczne jest zmierzenie wewnętrznych kąty enregonu wynosi 1260º / 9 = 140º.

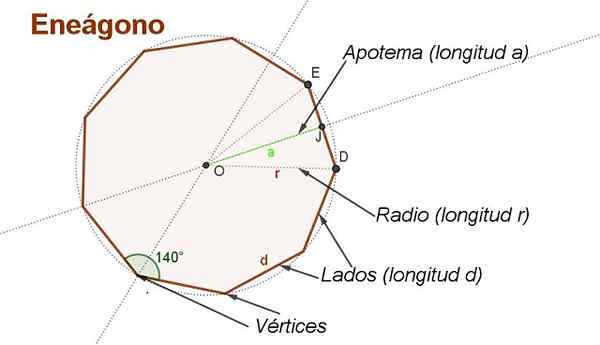Rysunek 2. Apothem, radio, boki, kąty i wierzchołki zwykłego enregonu. (Własne opracowanie)

Aby wydedukować formułę obszaru enregonu zwykłego z boku D Wygodne jest tworzenie niektórych konstrukcji pomocniczych, takich jak te pokazane na rycinie 2.

Centrum jest ALBO Rysowanie mediów dwóch sąsiednich stron. Centrum ALBO Equidista wierzchołków.

Promień długości R To segment przechodzi od centrum ALBO W wierzchołku Enegona. Radia pokazano na rycinie 2 Od I Oe długości R.

Może ci służyć: symetria

Apothem jest segmentem, który przechodzi od środka do punktu środkowego po jednej stronie ENEGON. Na przykład OJ To apothem, którego długość jest Do.

Obszar znanej strony i apothem

Rozważamy trójkąt ODA Z ryc. 2. Obszar tego trójkąta jest produktem jego podstawy Z według wysokości OJ podzielone przez 2:

Obszar ODA = (Od * OJ) / 2 = (D * a) / 2

Ponieważ w Eneregonie jest 9 trójkątów tego samego obszaru, stwierdza się, że obszar tego samego jest:

Obszar Enegon = (9/2) (D * a)

Obszar znanego enregonu

Jeśli znana jest tylko długość enregonu, konieczne jest znalezienie długości apothemu, aby móc zastosować wzór z poprzedniej sekcji.

Rozważamy trójkąt Oje Prostokąt w J (Patrz Rysunek 2). Jeśli zastosowany jest stosunek trygonometryczny momentu obrotowego, uzyskuje się go:

Więc(∡OEJ) = OJ / Np.

Kąt ∡oej = 140º / 2 = 70º, za bycie EO Bisektor kąta wewnętrznego Enegonu.

Oprócz, OJ To jest apothem długości Do.

Następnie jako J Jest to punkt środkowy Wyd Wynika, że Ex = d/2.

Zastępowanie powyższych wartości w związku stycznej to:

Tan (70º) = A / (d / 2).

Teraz usuwamy długość Apothem:

A = (d/2) Tan (70º).

Poprzedni wynik jest zastępowany w wzorze obszaru, aby uzyskać:

Obszar Enegon = (9/2) (D * a) = (9/2)( D * (d/2) Tan (70º))

Wreszcie istnieje formuła, która pozwala na uzyskanie stałego obszaru enregonu, jeśli znana jest tylko długość D jego stron:

Obszar Enegon = (9/4) d² Tan (70º) = 6 1818 D²

Obwód regularnego enregonu znany jest po boku

Obwód wielokąta jest sumą jego boków. W przypadku enregonu, jak każda z nich, mierzy długość D, Jego obwód będzie sumą dziewięciu razy D, to jest do powiedzenia:

Może ci służyć: równania wielomianowe

Obwód = 9 D

Obwód ENEGON Znał jego radio

Biorąc pod uwagę trójkąt Oje Prostokąt w J (Patrz rysunek 2), stosowany jest powód trygonometryczny:

CO (∡OEJ) = Np / Oe = (d / 2) / r

Gdzie jesteś uzyskany:

D = 2r CO (70º)

Podstawiając ten wynik, wzór obwodu jest uzyskiwany jako funkcja promienia enregonu:

Obwód = 9 D = 18 r cos (70º) = 6 1564 r

Jak zrobić regularny enregon

1- Aby zbudować regularny enregon, z regułą i kompasem, opiera się na obwodzie C To ogranicza Enegon. (Patrz Rysunek 3)

2- dwie prostopadłe linie są rysowane przez środek lub obwód. Następnie skrzyżowania a i b jednej z linii są oznaczone obwodem.

3- Z kompasem, czyniąc w środku w przechwytywaniu B i otwieranie równe promieniu BO.

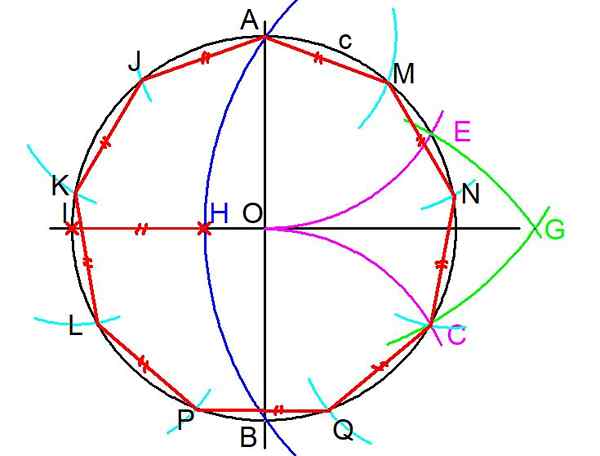Rysunek 3. Kroki, aby zbudować regularny engon. (Własne opracowanie)

4- Poprzedni krok jest powtarzany, ale wykonanie środka w A i Radio AO narysuje się łuk, który przechwytuje obwód C w punkcie E.

5- z otwieraniem prądu przemiennym i środkiem w łuku a obwód jest narysowany. Podobnie wraz z otwieraniem i środkiem B narysowanym kolejnym łukiem. Przecięcie tych dwóch łuków jest oznaczone jako G.

6- Making Center w g i otwieraniu GA narysuje się łuk, który przechwytuje oś wtórną (w tym przypadku poziomym) w punkcie H. Przecięcie osi wtórnej jest oznaczone oryginalnym obwodem c jako i.

7- Długość odcinka IH jest równa długości D z boku enregonu.

8- Z otworzeniem kompasu IH = D Centralne łuki są sukcesywnie przyciągane do Radio AJ, Centro J Radio AK, KL Radio KL i Centro L Radio LP.

Może ci służyć: transformacje liniowe: właściwości, jakie są użycie, typy, przykłady

9- Podobnie, zaczynając od A i po prawej stronie, Radio Arcos IH = D są rysowane na pierwotnych punktach C obwodu M, N, C i Q.

10- Wreszcie segmenty AJ, JK, KL, LP, AM, MN, NC, CQ i wreszcie PB są rysowane.

Należy zauważyć, że metoda konstrukcji nie jest całkowicie dokładna, ponieważ można zweryfikować, że ostatnia strona PB jest o 0,7% dłuższa niż inne strony. Do tej pory nie wiadomo, że metoda konstrukcji konstrukcyjnej i kompasu jest w 100% precyzyjna.

Przykłady

Niektóre przykłady rozwiązane zostaną omówione poniżej.

Przykład 1

Chcesz zbudować regularny enregon, którego strony mierzą 2 cm. Jaki radio powinien go ograniczyć, tak że przy zastosowaniu wcześniej opisanej konstrukcji uzyskano pożądany wynik?

Rozwiązanie:

We wcześniejszej sekcji wywnioskowano formułę, która odnosi promień R ograniczenionego obwodu z Regularnym Dégonem:

D = 2r CO (70º)

Oczyszczanie R z poprzedniego wyrażenia mamy:

R = D / (2 cos (70º)) = 1 4619 * D

Zastąpienie wartości d = 2 cm w poprzedniej wzorze OTRZYMANE jest promień 2,92 cm.

Przykład 2

Ile kosztuje obszar zwykłego enregonu bocznego 2 cm?

Rozwiązanie:

Aby odpowiedzieć na to pytanie, musisz odwołać się do wcześniej pokazanej formuły, która pozwala znaleźć obszar Enegona znanego długości D po jego stronie:

Obszar Enegon = (9/4) d² Tan (70º) = 6 1818 D²

Uzyskuje się wymianę D dla jego wartości 2 cm w wzorze przednim:

Obszar Enegon = 24,72 cm

Bibliografia

1. C. I. DO. (2003). Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematyka 2. Grupa redakcyjna Patria.
3. Freed, k. (2007). Odkryj wielokąty. Benchmark Education Company.
4. Hendrik, v. (2013). Uogólnione wielokąty. Birkhäuser.
5. Iger. (S.F.). Matematyka pierwszy semestr Tacaná. Iger.
6. Jr. Geometria. (2014). Wielokąty. Lulu Press, Inc.
7. Miller, Heeren i Hornsby. (2006). Matematyka: rozumowanie i aplikacje (wydanie dziesiąta). Edukacja Pearsona.
8. Patiño, m. (2006). Matematyka 5. Progreso redakcyjne.