W jakich sytuacjach są funkcje liniowe i kwadratowe?

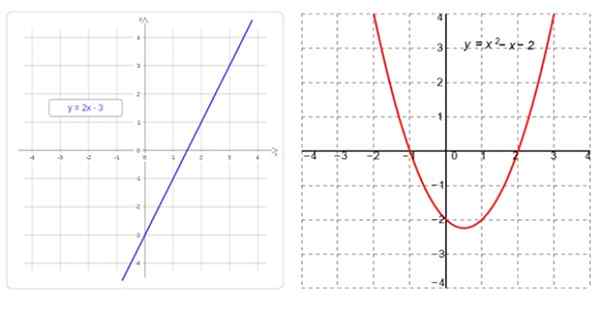
Po lewej stronie funkcja liniowa, której wykres jest linią prostą, a po prawej, funkcja kwadratowa, której wykres jest parabola. Źródło: f. Zapata

Jakie są funkcje liniowe i kwadratowe?

Funkcje liniowe i funkcje kwadratowe są funkcjami należącymi do grupy funkcji wieloparomicznych. Służą one do modelowania różnych sytuacji, takich jak zależność między objętością i wagą ciała, ilość i koszt produktu, pozycja w porównaniu z czasem i nie tylko.

Ogólnie rzecz biorąc, funkcja to związek, który łączy dwie zmienne i może być używana do modelowania świata rzeczywistego. Funkcje wielomarne, jak sama nazwa wskazuje, są wyrażane przez wielomian, którego ogólną formą jest:

f (x) = a_NX^N + Do _N-1X ^N-1 + Do_X-2X^N-2 +… Do_albo

Gdzie n jest liczbą naturalną, liczby₀, Do₁, Do₂,… Do_N Są prawdziwe, aby₀ Jest to niezależny termin i do_N, Jest to współczynnik towarzyszący najwyższej mocy. Wartość n wskazuje rodzaj funkcji, dla n = 1 funkcja jest liniowa, podczas gdy dla n = 2 funkcja jest kwadratowa.

W pierwszym z tych przypadków ogólne wyrażenie jest zmniejszone do:

f (x) = a₁x + a_albo

A w drugim przypadku pozostaje tak:

f (x) = a₂X² + Do₁x + a_albo ;   (Do₂≠ 0)

Wykresy funkcji wielomianowych są ciągłe, to znaczy nie doświadczają nagłych skoków ani pęknięć, a tym samym miękkie zachowanie, bez nieprawidłowości. Dlatego są one obserwowane w modelowaniu wielu sytuacji nauki, ekonomii i innych obszarów ludzkiej wiedzy.

Następnie interesujące się wzajemne zastosowania są szczegółowo opisane.

Sytuacje, w których pojawiają się funkcje liniowe

Funkcja liniowa jest reprezentowana algebraicznie przez:

f (x) = a₁x + a_albo

Lub równoważnie:

f (x) = MX + B

Jego charakterystyczna funkcja polega na tym, że jego wykres jest linią prostą. Wartość M, który jest współczynnikiem X, reprezentuje kolczyk tej linii i daje miarę tego, jak jest to skłonne.

Może ci służyć: programowanie nieliniowe: metody i ćwiczenia

Nachylenie może być dodatnie, ujemne lub zerowe, ale zawsze jest stałe, to znaczy jego kurs wymiany pozostaje niezmieniony.

Linia nachylenia 0 jest całkowicie pozioma, dodatnie nachylenie wskazuje na podwyższenie lub wzrost (jeśli jedna z zmiennych wzrasta, druga również, zawsze w tej samej szybkości) i na koniec ujemne nachylenie wskazuje na spadek (jako A zmiennych wzrasta, drugi maleje).

Wartość B, Ze swojej części reprezentuje cięcie lub przecięcie linii z osą pionową. Tak B = 0, Linia przechodzi przez pochodzenie układu współrzędnych.

Modelowanie przykładów z funkcjami liniowymi

1. Jednolity ruch prostoliniowy

Równanie, które łączy pozycję X i czas T telefonu komórkowego, w jednolitym ruchu prostoliniowym, jest liniowe:

x (t) = v⋅t + x_albo

Gdzie v, nachylenie linii, jest prędkość telefonu komórkowego, która pozostaje stała przez cały ruch i x_albo to początkowa pozycja.

2. Gęstość

Gęstość obiektu lub substancji, która ustanawia związek między masą a objętością. Wzywając ρ do gęstości (czyta „rho”), m do ciasta i v do głośności, masz:

Oczyszczając ciasto pod względem objętości, jest uzyskiwane:

M = ρv

Podczas wykresu ciasta w zależności od objętości uzyskuje się linię prostą, której nachylenie jest gęstością obiektu lub substancji.

3. Długość obwodu

Kontur koła lub jego długości jest proporcjonalny do jego promienia. Oznacza to, że im większy promień, tym większy kontur obwód, zgodnie z równaniem:

Może ci służyć: współczynnik korelacji: wzory, obliczenia, interpretacja, przykład

C = 2πr

Gdzie C jest konturem lub długością, R jest radiem, a π (odczytuje „PI”) jest stałą, której przybliżona wartość to πAMP3.14 ..

4. Koszt wysłania paczki

Ponieważ łatwo się wywnioskować, cięższy lub nieporęczny jest droższy pakiet to transport. Firmy, które są poświęcone transportowi ładunków, modelują swoje ceny zgodnie z pewnymi zasadami, na przykład:

C (x) = 2.75x

W tym równaniu C (x) to koszt dolara na wysłanie pakietu, którego waga to x funty. Stała wartość 2.75 ma jednostki dolara/funta (koszt jednostkowy).

Sytuacje, w których pojawiają się funkcje kwadratowe

Algebraicznie funkcja kwadratowa jest reprezentowana przez:

f (x) = a₂ X² + Do₁ x + a_albo

Ze stanem współczynnika do₂ Różni się od 0. Charakteryzuje się jego wykresem w kształcie paraboli, którego osi osiowej lub osi symetrii jest pionowy (równolegle do osi y)))).

Przecięcie przypowieści i wspomnianej osi jest punktem zwanym wierzchołkiem. Jeśli przypowieść otworzy się (a₂ > 0), wierzchołek jest jego minimalnym punktem, a jeśli się otworzy (a₂ < 0), es el máximo.

Na osi symetrii znajduje się szczególny punkt, który określa krzywiznę paraboli. Jeśli na światło słoneczne wpłynie na lustro paraboliczne, promienie zostaną odbite na powierzchni, zbieżne w ogrzewaniu, które jest natychmiast ogrzewane.

Modelowanie przykładów z funkcjami kwadratowymi

1. Wysokość pocisku uruchomiona pionowo

Pocisk to dowolny obiekt, do którego zapewniana jest prędkość początkowa, a następnie zwolniona, pod działaniem grawitacji. Jeśli początkowa prędkość jest pionowa, wielkość v₀ i skierowany, obiekt wzrośnie do maksymalnej wysokości, a następnie zejdzie.

Może ci służyć: homotecia

Równanie wysokości h jako funkcji czasu t jest:

H (t) = −4.9 t²+v₀ T

Gdzie poczucie pionowego jest uznane za pozytywne, a pionowe ujemne.

2. Trajektoria poziomego lub ukośnego pocisku

Jeśli do pocisku zostanie dostarczona pozioma lub ukośna prędkość początkowa, opisuje trajektorię paraboliczną, którą można reprezentować poprzez funkcję kwadratową, jak opisano wcześniej.

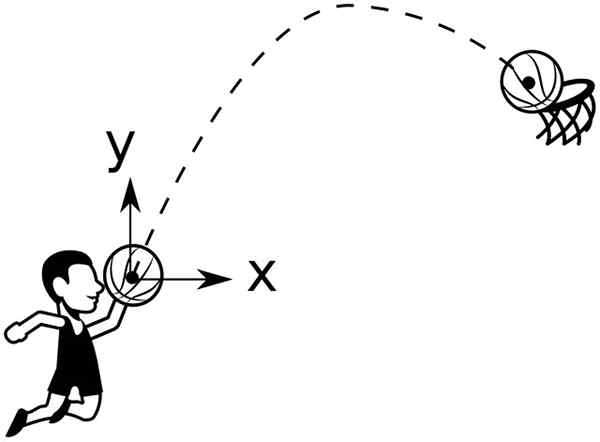KALL BAKUS opisuje trajektorię paraboliczną, która ma zostać wrzucona do kosza. Źródło: Wikimedia Commons

Na przykład piłka wyrzucona z wysokości i₀, Kąt formowania θ₀ Jeśli chodzi o poziome, ma trajektorię podaną przez:

Z G jako przyspieszenie grawitacji, które może około 10 m/s². Na przykład kopnięcie piłki nożnej z ziemi (i₀ = 0), z początkową prędkością 6 m/s i kątem 45º w odniesieniu do poziomego, będzie miał trajektorię podaną przez następującą przypowieść:

3. Obszar koła

Im wyższy promień koła, tym większy będzie jego obszar. Rzeczywiście, powierzchnia okręgu jest proporcjonalna do kwadratu promienia r, stała proporcjonalności jest liczba π:

A = πr²

4. Skuteczność reklamy

Im bardziej to widzą, tym bardziej skuteczne reklamy komercyjne. Skuteczność E, w skali od 0 do 10, od jednego zawiadomienia można modelować zgodnie z następującą funkcją kwadratową:

Bibliografia 

1. Funkcje wieloparomiczne. Odzyskane z zasobów.Edukacja.Jest.
2. Larson, r. (2012). Przedłużanie. 8. wydanie. Cengage Learning.
3. Miller, c. (2013). Matematyka: rozumowanie i aplikacje. 12. wydanie. Edukacja Pearsona.
4. Stewart, J. (2012). Przedłużanie. Matematyka do obliczeń. 6th. wydanie. Cengage Learning.
5. Zill, d. (2008). Prefrecment z postępami obliczeniowymi. 4. wydanie. McGraw Hill.