Ogólne równanie linii, której nachylenie jest równe 2/3

Ogólne równanie linii L jest następujące: AX+przez+c = 0, gdzie a, b i c są stałe, x jest zmienną niezależną e i zmienną zależną.

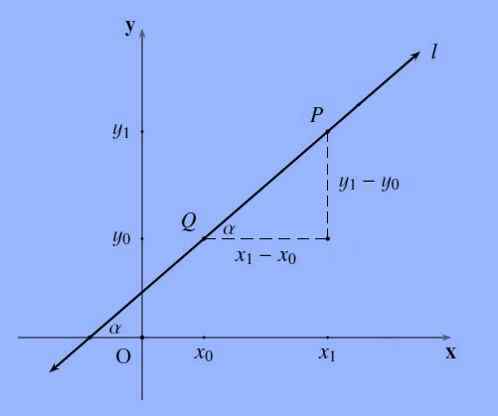
Nachylenie linii, oznaczone ogólnym sposobem literą M, która przechodzi przez punkty p = (x1, y1) i q = (x0, y0) jest następującym ilorazem m: = (y1-y0)/(x1 -X0).

Nachylenie linii prostej reprezentuje nachylenie; Powiedział bardziej formalnie, nachylenie linii jest stycznie kątem, że ten kształt z osi x.

Należy zauważyć, że kolejność nazywanych punktów jest obojętna, ponieważ (y0-y1)/(x0-x1) =-(y1-y0)/(-(x1-x0)) = (y1-y0) /(X1-x0).

Oczekująca linia

Jeśli znane są dwa punkty, przez które przechodzi linia, łatwo jest obliczyć jej nachylenie. Ale co się stanie, jeśli te punkty nie są znane?

Biorąc pod uwagę ogólne równanie linii AX+przez+c = 0, musi ona.

Jakie jest ogólne równanie linii, której nachylenie wynosi 2/3?

Ponieważ nachylenie linii wynosi 2/3, równość jest ustalana -a/b = 2/3, co może zobaczyć, że a = -2 i b = 3. Tak że ogólne równanie linii z nachyleniem równym 2/3 wynosi -2x+3y+c = 0.

Należy wyjaśnić, że jeśli zostaniesz wybrany a = 2 i b = -3, to samo równanie zostanie uzyskane. Rzeczywiście, 2x -3y+c = 0, co jest równe poprzednim mnożonym przez -1. Znak C nie ma znaczenia, ponieważ jest to ogólna stała.

Inną obserwacją, którą można dokonać, jest to, że dla A = -4 i B = 6 otrzymuje się ta sama linia, chociaż jego ogólne równanie jest różne. W takim przypadku ogólne równanie wynosi -4x+6y+c = 0.

Czy istnieją inne sposoby znalezienia ogólnego równania linii?

Odpowiedź brzmi tak. Jeśli nachylenie linii jest znane, istnieją dwie formy, dodatkowe do poprzedniej, aby znaleźć ogólne równanie.

W tym celu stosowane są równanie i równanie cięcia.

-Zakładające punkty równanie: jeśli M jest nachyleniem linii i p = (x0, y0) punkt, w którym przechodzi, to równanie y-y0 = m (x-x0) nazywane jest równanie nakładającym punkt.

-Równanie nakładające do cięcia: jeśli M jest nachyleniem linii i (0, b) jest cięciem linii z osą y, wówczas równanie y = mx+b nazywane jest równanie nakładające się na cięcie.

Korzystając z pierwszego przypadku, uzyskuje się, że wyraża równanie linii, której nachylenie wynosi 2/3, jest podane przez wyrażenie y-y0 = (2/3) (x-x0).

Aby osiągnąć ogólne równanie, wszystkie terminy są mnożone przez 3 po obu stronach i są zgrupowane razem, uzyskując w ten sposób -2x+3y+(2 × 0-3y0) = 0 jest ogólnym równaniem linii, gdzie C = 2 × 2 × 0-3Y0.

Jeśli używany jest drugi przypadek, uzyskuje się, że wycinanie równania linii, której nachylenie wynosi 2/3 to y = (2/3) x+b.

Ponownie, pomnożenie 3 po obu stronach i grupowanie wszystkich zmiennych, jest uzyskiwane -2x+3y -3b = 0. To ostatnie jest ogólnym równaniem linii, w której c = -3b.

W rzeczywistości, uważnie przyjrzeniu obu przypadków, można zauważyć, że drugi przypadek jest po prostu szczególnym przypadkiem pierwszego (gdy x0 = 0).