Normalny rozkład formuły, cechy, przykład, ćwiczenia

 normalna dystrybucja o Rozkład Gaussa jest rozkładem prawdopodobieństwa w zmiennej ciągłej, w której funkcja gęstości prawdopodobieństwa opisuje wykładniczą funkcję argumentu kwadratowego i negatywnego, co powoduje rozdrobnioną formę.

Nazwa rozkładu normalnego wynika z faktu, że ten rozkład jest ten, który jest stosowany do największej liczby sytuacji, w których pewna ciągła zmienna losowa jest zaangażowana w daną grupę lub populację.

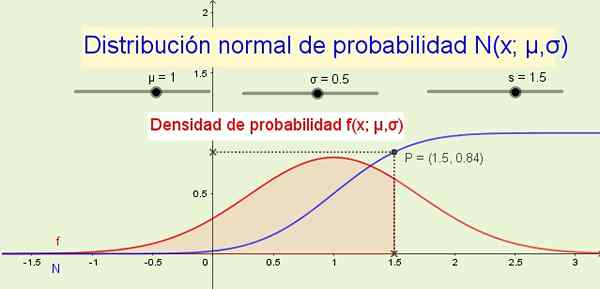
Rysunek 1. Rozkład normalny n (x; μ, σ) i jego gęstość prawdopodobieństwa f (s; μ, σ). (Własne opracowanie)

Jako przykłady zastosowania rozkładu normalnego: wysokość mężczyzn lub kobiet, różnice w zakresie pewnej wielkości fizycznej lub w mierzalnych cechach psychologicznych lub socjologicznych, takich jak iloraz intelektualny lub nawyki konsumpcyjne określonego produktu.

Z drugiej strony nazywa się to dystrybucją Gaussa lub Bell Gaussa, ponieważ to ten niemiecki geniusz matematyczny przypisuje się jego odkrycie za użycie, jakie podał do opisu błędu statystycznego pomiarów astronomicznych w 1800 roku.

Twierdzi się jednak, że ta dystrybucja statystyczna została wcześniej opublikowana przez innego wielkiego matematyka pochodzenia francuskiego, podobnie jak Abraham de Moivre, w 1733 roku.

[TOC]

Formuła

Do funkcji rozkładu normalnego w zmiennej ciągłej X, Z parametrami μ I σ Jest to oznaczone przez:

N (x; μ, σ)

I wyraźnie jest tak napisany:

N (x; μ, σ) = ∫_-∞^X f (s; μ, σ) ds

Gdzie f (u; μ, σ) Jest to funkcja gęstości prawdopodobieństwa:

f (s; μ, σ) = (1/(σ√ (2π)) exp ( - s²/(2σ²)

Stała, która zwielokrotnia funkcję wykładniczą w funkcji gęstości prawdopodobieństwa, jest nazywana stałą normalizacyjną i została wybrana w taki sposób, aby:

N (+∞, μ, σ) = 1

Poprzednie wyrażenie zapewnia prawdopodobieństwo, że zmienna losowa X być między -∞ i +∞ albo 1, to jest 100% prawdopodobieństwo.

Parametr μ Jest to średnia arytmetyczna ciągłej zmiennej losowej x i σ Odchylenie standardowe lub pierwiastek kwadratowy wariancji tej samej zmiennej. W przypadku tego μ = 0 I σ = 1 Masz normalny rozkład standardowy lub rozkład normalny typowy: 

N (x; μ = 0, σ = 1)

Charakterystyka rozkładu normalnego

1- Jeśli losowa zmienna statystyczna wynika z normalnego rozkładu gęstości prawdopodobieństwa F (s; μ, σ), Większość danych jest pogrupowana wokół średniej wartości μ I są rozproszeni wokół nich, aby tuż nad danymi były pomiędzy μ - σ I μ + σ. 

Może ci służyć: Częstotliwość bezwzględna: wzór, obliczenia, rozkład, przykład

2- Odchylenie standardowe σ To zawsze pozytywne.

3- Forma funkcji gęstości F Przypomina funkcję dzwonka, więc ta funkcja jest często nazywana funkcją gaussa lub gaussa. 

4- W dystrybucji Gaussa średnia, mediana i moda zbieżą się.

5- Punkty fleksji funkcji gęstości prawdopodobieństwa są dokładnie znalezione w μ - σ I μ + σ.

6- Funkcja F jest symetryczna w odniesieniu do osi, która przechodzi według jej średniej wartości μ I masz zero asymptotycznie dla x ⟶ +∞ i x ⟶ -∞.

7- Wyższa wartość σ większa dyspersja, szum lub dystansowanie danych wokół średniej wartości. To znaczy Greater σ Kształt dzwonka jest bardziej otwarty. Zamiast σ Małe wskazuje, że kości płynęły do ​​średniej, a kształt dzwonka jest bardziej zamknięty lub spiczasty.

8- Funkcja rozkładu N (x; μ, σ) wskazuje prawdopodobieństwo, że zmienna losowa jest mniejsza lub równa X. Na przykład na rycinie 1 (powyżej) prawdopodobieństwo p zmienną X jest mniejsze lub równe 1.5 wynosi 84% i odpowiada obszarowi w ramach funkcji gęstości prawdopodobieństwa f (x; μ, σ) Od -∞ do X.

Interwały zaufania

9- Jeśli dane są zgodne z rozkładem normalnym, wówczas 68,26% z nich jest pomiędzy μ - σ I μ + σ.

10- 95,44% danych następujących po rozkładowi normalnym jest pomiędzy μ - 2σ I μ + 2σ.

11- 99,74% danych, które następują po rozkładowi normalnym μ - 3σ I μ + 3σ.

12- Jeśli zmienna losowa X Postępuj zgodnie z rozkładem N (x; μ, σ), Następnie zmienna

Z = (x - μ) / σ  Postępuj zgodnie ze standardowym rozkładem normalnym  N (z; 0,1).

Zmiana zmiennej X do z Nazywa się to standaryzacja lub typowanie i jest bardzo przydatne w momencie zastosowania standardowych tabel rozkładu do danych, które następują po normalnym niestandardowym rozkładowi.

Zastosowania rozkładu normalnego

Aby zastosować rozkład normalny, konieczne jest przejście przez obliczenie całki gęstości prawdopodobieństwa, która z analitycznego punktu widzenia nie jest łatwa i nie zawsze jest dostępny program komputerowy, który umożliwia jego obliczenia numeryczne. W tym celu stosowane są standardowe lub typowe tabele wartości, co jest niczym więcej niż rozkładem normalnym w przypadku μ = 0 i σ = 1.

Może ci służyć: połączone operacje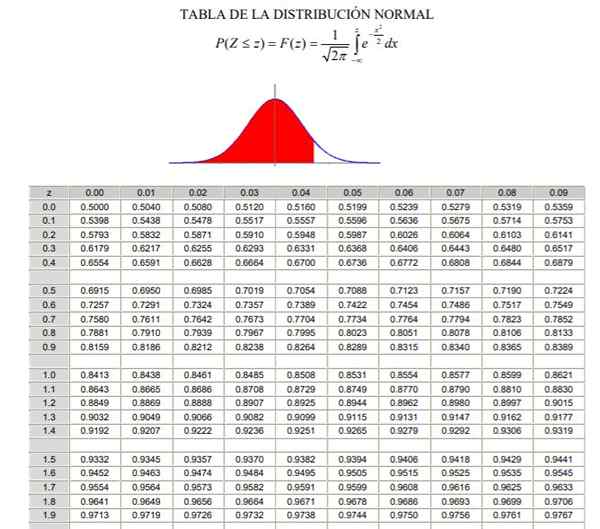Tabela rozkładu normalnego (część 1/2) 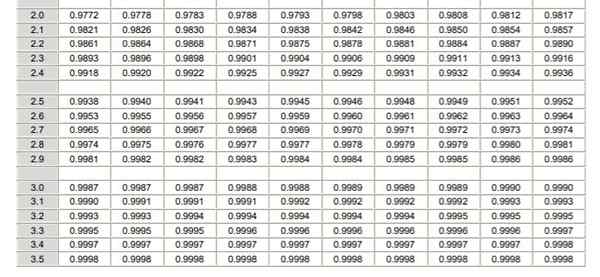Tabela rozkładu normalnego (część 2/2)

Należy zauważyć, że tabele te nie zawierają wartości ujemnych. Jednak przy użyciu właściwości symetrii funkcji gęstości prawdopodobieństwa Gaussa można uzyskać odpowiednie wartości. W rozwiązanym ćwiczeniu pokazanym poniżej użycie tabeli jest wskazane w tych przypadkach.

Przykład

Załóżmy, że masz losowy zestaw danych x, który przestrzegał normalnego rozkładu 10 i odchylenia standardowego 2. Poproszono o znalezienie prawdopodobieństwa:

a) Zmienna losowa x jest mniejsza lub równa 8.

b) jest mniejsze lub równe 10.

c) ta zmienna x jest poniżej 12.

d) prawdopodobieństwo, że wartość x wynosi od 8 do 12.

Rozwiązanie:

a) Aby odpowiedzieć na pierwsze pytanie, które musisz po prostu obliczyć:

N (x; μ, σ)

Z x = 8, μ = 10 I σ = 2. Zdajemy sobie sprawę, że jest to całka, która nie ma rozwiązania analitycznego w funkcjach elementarnych, ale rozwiązanie jest wyrażone zgodnie z funkcją błędu ERF (x).

Z drugiej strony istnieje możliwość rozwiązania całki w sposób numeryczny, co robi wiele kalkulatorów, arkuszy kalkulacyjnych i programów komputerowych, takich jak Geogebra. Poniższy rysunek pokazuje rozwiązanie numeryczne odpowiadające pierwszemu przypadkowi:

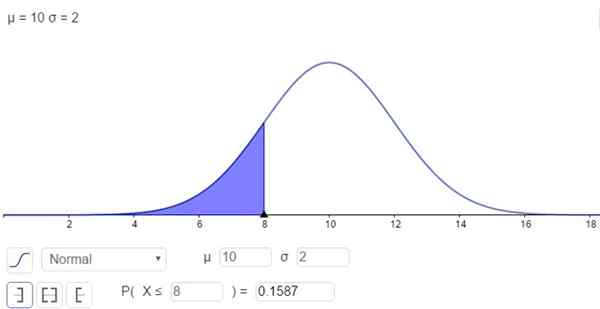Rysunek 2. Gęstość prawdopodobieństwa f (x; μ, σ). Zacieniony obszar reprezentuje P (x ≤ 8). (Własne opracowanie)

Odpowiedź brzmi, że prawdopodobieństwo, że x jest poniżej 8, wynosi:

P (x ≤ 8) = n (x = 8; μ = 10, σ = 2) = 0,1587

b) W tym przypadku chodzi o znalezienie prawdopodobieństwa, że ​​zmienna losowa x będzie poniżej średniej, która w tym przypadku jest warta 10. Odpowiedź nie wymaga żadnych obliczeń, ponieważ wiemy, że połowa danych jest poniżej średniej, a druga połowa powyżej średniej. Dlatego odpowiedź brzmi:

P (x ≤ 10) = n (x = 10; μ = 10, σ = 2) = 0,5

c) Aby odpowiedzieć na to pytanie, które musisz obliczyć N (x = 12; μ = 10, σ = 2), które można wykonać za pomocą kalkulatora, który ma funkcje statystyczne lub przez oprogramowanie takie jak Geogebra:

Może ci służyć: dzielnicy 8: co to jest i łatwe wyjaśnienie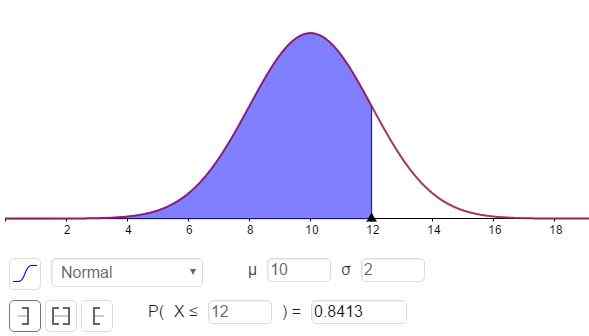Rysunek 3. Gęstość prawdopodobieństwa f (x; μ, σ). Zacieniony obszar reprezentuje P (x ≤ 12). (Własne opracowanie)

Odpowiedź na część C można zobaczyć na rycinie 3 i jest:

P (x ≤ 12) = n (x = 12; μ = 10, σ = 2) = 0,8413.

d) Aby znaleźć prawdopodobieństwo, że zmienna losowa x wynosi od 8 do 12, możemy użyć wyników części A i C w następujący sposób:

P (8 ≤ x ≤ 12) = p (x ≤ 12) - p (x ≤ 8) = 0,8413 - 0,1587 = 0,6826 = 68,26.

Ćwiczenie rozwiązane

Średnia cena akcji spółki wynosi 25 USD, a odchylenie standardowe w wysokości 4 USD. Określ prawdopodobieństwo:

a) Działanie ma koszt mniejszy niż 20 USD.

b) ma koszt przekraczający 30 USD.

c) Cena wynosi od 20 do 30 USD.

Użyj typów normalnych rozkładu, aby znaleźć odpowiedzi.

Rozwiązanie:

Aby skorzystać z tabel, konieczne jest przejście do zmiennej znormalizowanej lub typowej:

20 USD w znormalizowanej zmiennej jest równe Z = (20 USD - 25 USD) / 4 USD = -5/4 = -1,25 i 

30 USD w znormalizowanej zmiennej jest równe Z = (30 USD - 25 USD) / 4 USD = +5/4 = +1,25.

a) 20 USD jest równoważne -1,25 w znormalizowanej zmiennej, ale tabela nie ma wartości ujemnych, więc umieszczamy wartość +1,25, która pokazuje wartość 0,8944.

Jeśli ta wartość zostanie odjęta 0,5, wynikiem będzie obszar od 0 do 1,25, który, nawiasem mówiąc, jest identyczny (przez symetrię) z obszarem między -1.25 i 0. Wynik odejmowania wynosi 0,8944 - 0,5 = 0,3944, który jest obszarem między -1.25 i 0.

Ale zainteresowania obszaru od -ślistra do -1,25, które wyniesie 0,5 -0,3944 = 0,1056. Stwierdzono zatem, że prawdopodobieństwo, że działanie jest poniżej 20 USD, wynosi 10,56%.

b) 30 USD w typowej zmiennej Z wynosi 1,25. Dla tej wartości w tabeli pojawia się liczba 0,8944, która odpowiada obszarowi od -∞ do +1,25. Obszar między +1.25 y +∞ wynosi (1 - 0,8944) = 0,1056. Innymi słowy, prawdopodobieństwo, że akcja kosztuje ponad 30 USD, wynosi 10,56%.

c) prawdopodobieństwo, że akcja ma koszt od 20 do 30 USD, zostanie obliczone w następujący sposób:

100% -10,56% - 10,56% = 78,88%

Bibliografia

1. Statystyki i prawdopodobieństwo. Normalna dystrybucja. Źródło: ProjectOdescartes.org
2. Geogebra. Klasyczny Geogebra, obliczanie prawdopodobieństwa. Odzyskane z Geogebry.org
3. Mathworks. Dystrybucja Gaussa. Odzyskane z: jest.Mathworks.com
4. Mendenhall, w. 1981. Statystyka administracji i ekonomii. 3. wydanie. Grupa redakcyjna Iberoamerica.
5. Stat Trek. Naucz się statystyki. Dystrybucja Poissona. Odzyskane z: Stattrek.com,
6. TRIOLA, m. 2012. Statystyka podstawowa. 11. Wyd. Edukacja Pearsona.
7. University of Vigo. Główne ciągłe dystrybucje. Odzyskany z: anapg.strony internetowe.Uvigo.Jest
8. Wikipedia. Normalna dystrybucja. Odzyskane z: jest.Wikipedia.org