Rozkład F Charakterystyka i ćwiczenia rozwiązane

Rozkład f o Dystrybucja Fisher-Enedecor jest używana do porównywania wariancji dwóch różnych lub niezależnych populacji, z których każda jest zgodna z rozkładem normalnym.

Rozkład, który następuje po wariancji zestawu próbek pojedynczej normalnej populacji, jest rozkład ji-kwadrat (Χ²) stopnia n-1, jeśli każda z próbek zestawu ma n elementy.

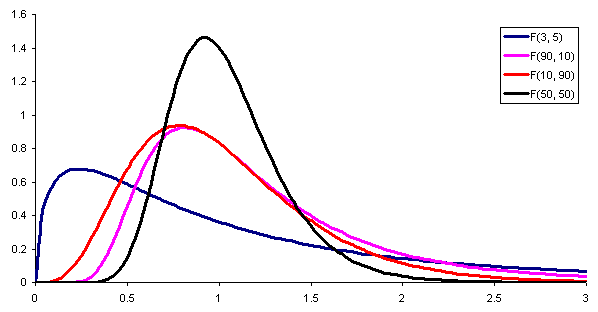
Rysunek 1. Oto gęstość prawdopodobieństwa rozkładu F z różnymi kombinacjami parametrów (lub stopni swobody) odpowiednio licznika i mianownika. Źródło: Wikimedia Commons.

Aby porównać wariancje dwóch różnych populacji, należy zdefiniować statystyczny, to znaczy pomocnicza zmienna losowa, która pozwala dostrzec, czy obie populacje mają tę samą wariancję.

Ta zmienna pomocnicza może być bezpośrednio ilorazem wariancji próbki każdej populacji, w którym to przypadku, jeśli wspomniany iloraz jest blisko jednostki, dowodzi, że obie populacje mają podobne wariancje.

[TOC]

Statystyka F i jego rozkład teoretyczny

Zmienna losowa F lub statystyczna F zaproponowana przez Ronalda Fishera (1890–1962) jest tym, który częściej stosował do porównania wariancji dwóch populacji i jest zdefiniowana w następujący sposób:

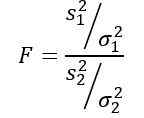
Bycie s² Wariancja próbki i σ² Wariancja populacji. Aby rozróżnić każdą z dwóch grup populacji, odpowiednio stosuje się subskrypcje 1 i 2.

Wiadomo, że rozkład ji-kwadrat z (n-1) stopnie wolności jest tym, który następuje po zmiennej pomocniczej (lub statystycznej), która jest zdefiniowana poniżej:

X² = (N-1) s² / σ².

Dlatego statystyka F jest zgodna z rozkładem teoretycznym podanym przez następujący wzór:

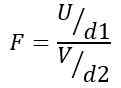
Istnienie LUB Rozkład ji-kwadrat z D1 = N1 - 1 stopnie swobody dla populacji 1 i V Rozkład ji-kwadrat z D2 = N2 - 1 stopnie swobody dla ludności 2.

Może ci służyć: algebra wektorowa

Stosunek zdefiniowany w ten sposób jest nowym rozkładem prawdopodobieństwa, znanym jako Rozkład f z D1 stopnie swobody w licznikach i D2 stopnie wolności w mianowniku.

Średnia, moda i wariancja dystrybucji f

Połowa

Średni rozkład F jest obliczany w następujący sposób:

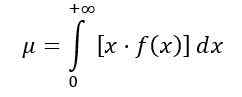
Będąc f (x) gęstość prawdopodobieństwa rozkładu f, co pokazano na rycinie 1 dla kilku kombinacji parametrów lub stopni swobody.

Możesz napisać gęstość prawdopodobieństwa f (x) w zależności od funkcji γ (funkcja gamma):

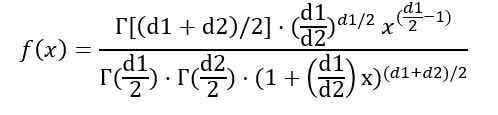
Po wskazaniu całki wcześniej stwierdzono, że średnia rozkładu F ze stopniami swobody (D1, D2) wynosi: IS: IS: IS:

μ = D2 / (D2 - 2) z D2> 2

Gdzie to pokazuje, co ciekawe, średnia nie zależy od stopni wolności D1 licznika.

Moda

Z drugiej strony moda zależy od D1 i D2 i jest podana przez:

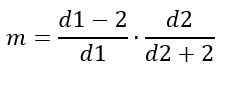
Dla D1> 2.

Wariancja rozkładu f

Wariancja σ² dystrybucji F jest obliczane na podstawie całki:

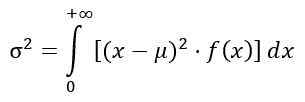
Uzyskanie:

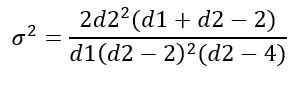
Zarządzanie dystrybucją f

Podobnie jak inne ciągłe rozkłady prawdopodobieństwa, które obejmują skomplikowane funkcje, zarządzanie dystrybucją F odbywa się według tabel lub oprogramowania.

Tabele dystrybucji f

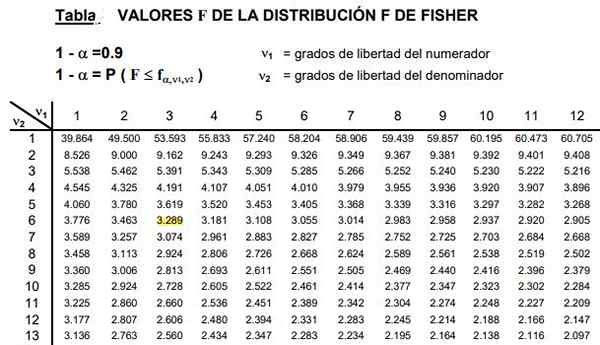Rysunek 2. Pokazana jest część tabeli rozkładu F, która jest zwykle bardzo obszerna, ponieważ istnieje szeroka kombinacja możliwych stopni swobody D1 i D2.

Tabele obejmują dwa parametry lub stopnie swobody dystrybucji f, kolumna wskazuje stopień swobody licznika i rząd stopień swobody mianownika.

Może ci służyć: nierówność trójkąta: demonstracja, przykłady, rozwiązane ćwiczenia

Ryc. 2 pokazuje odcinek tabeli rozkładu F dla przypadku a poziom istotności 10%, to znaczy α = 0,1. Wartość F jest podświetlana, gdy D1 = 3 i D2 = 6 z poziom zaufania 1- α = 0,9 to 90%.

Oprogramowanie do dystrybucji f

Jeśli chodzi o oprogramowanie, które zarządza dystrybucją F, istnieje duża różnorodność, od arkuszy kalkulacyjnych Przewyższać nawet wyspecjalizowane pakiety, takie jak Minitab, SPSS I R Wymienić niektóre z najbardziej znanych.

Należy zauważyć, że oprogramowanie geometrii i matematyki Geogebra Ma narzędzie statystyczne, które obejmuje główne rozkłady, w tym dystrybucja f. Rysunek 3 pokazuje rozkład F dla przypadku D1 = 3 i D2 = 6 poziom zaufania 90%.

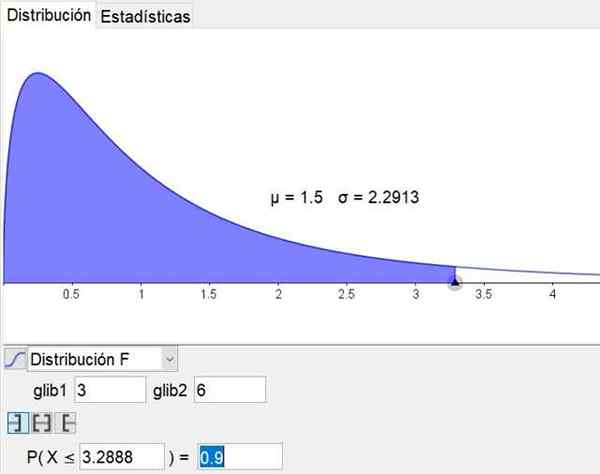Rysunek 3. Rozkład F jest pokazany dla przypadku D1 = 3 i D2 = 6 z poziomem ufności 90%, uzyskanym przez narzędzie statystyczne Geogebra. Źródło: Geogebra.org

Rozwiązane ćwiczenia

Ćwiczenie 1

Rozważ dwie próbki populacji o tej samej wariancji populacji. Jeśli próbka 1 ma rozmiar N1 = 5, a próbka 2 ma rozmiar N2 = 10, określ prawdopodobieństwo teoretyczne, że stosunek jej odpowiednich wariancji jest mniejszy lub równy 2.

Rozwiązanie

Należy pamiętać, że statystyka F jest definiowana jako:

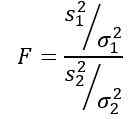
Ale powiedziano nam, że wariancje ludności są takie same, więc do tego ćwiczenia ma zastosowanie:

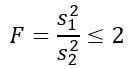
Jak chcesz poznać teoretyczne prawdopodobieństwo, że ten stosunek wariancji próbki jest mniejszy lub równy 2, musimy znać obszar pod dystrybucją F między 0 a 2, co można uzyskać za pomocą tabel lub oprogramowania. W tym celu należy wziąć pod uwagę, że wymagany rozkład F ma d1 = n1 - 1 = 5 - 1 = 4 i d2 = n2 - 1 = 10 - 1 = 9, to znaczy rozkład f o stopniach swobody (4, 9).

Może ci służyć: seria mocy: przykłady i ćwiczenia

Używając narzędzia statystycznego Geogebra Ustalono, że obszar ten wynosi 0.82, więc stwierdza się, że prawdopodobieństwo, że stosunek wariancji próbki jest mniejszy lub równy 2, wynosi 82%.

Ćwiczenia 2

Istnieją dwa cienkie procesy produkcyjne. Zmienność grubości musi być jak najwięcej. Pobrane są 21 próbek każdego procesu. Próbka procesu ma odchylenie standardowe 1,96 mikronów, podczas gdy proces B ma odchylenie standardowe 2,13 mikronów. Który z procesów ma niższą zmienność? Użyj 5% poziomu odrzucenia.

Rozwiązanie

Dane są następujące: SB = 2,13 z NB = 21; SA = 1,96 z Na = 21. Oznacza to, że musisz pracować z rozkładem F (20, 20) stopni wolności.

Hipoteza zerowa oznacza, że ​​wariancja populacji obu procesów jest identyczna, to znaczy σa^2 / σb^2 = 1. Alternatywna hipoteza oznaczałaby różne wariancje populacji.

Następnie, przy założeniu identycznych wariancji populacji, definiuje się statystyka F obliczona jako: fc = (sb/sa)^2.

Ponieważ poziom odrzucenia został przyjęty jako α = 0,05, wówczas α/2 = 0,025

Rozkład f (0.025; 20,20) = 0,406, podczas gdy F (0.975; 20,20) = 2,46.

Dlatego hipoteza zerowa będzie prawdą, jeśli F Obliczono: 0,406 ≤ FC ≤ 2,46. W przeciwnym razie hipoteza zerowa jest odrzucona.

Jak fc = (2,13/1,96)^2 = 1,18 stwierdza się, że statystyka FC jest w zakresie akceptacji hipotezy zerowej z pewnością 95%. Innymi słowy, z pewnością 95% oba procesy produkcyjne mają tę samą wariancję populacji.

Bibliografia

1. F Test dla niezależności. Odzyskany z: saylordotorg.Github.Io.
2. Med Wave. Statystyki zastosowane do nauk o zdrowiu: test f. Odzyskany z: Medwave.Cl.
3. Prawdopodobieństwa i statystyki. Rozkład f. Źródło: prawdopodobieństwa i.com.
4. TRIOLA, m. 2012. Statystyka podstawowa. 11. Wydanie. Addison Wesley.
5. Unam. Rozkład f. Odzyskany z: doradczy.Cuautitlan2.Unam.MX.
6. Wikipedia. Rozkład f. Odzyskane z: jest.Wikipedia.com