Matematyka

Miary zmienności

Miary zmienności
Rysunek 1.- Najbardziej znane miary zmienności. Źródło: f. Zapata.

Jakie są miary zmienności?

Miary zmienności, Nazywane również miarami dyspersji, są to wskaźniki statystyczne, które wskazują, jak bliskie lub zdalne znaleziono dane o średniej arytmetycznej. Jeśli dane są zbliżone do średniej, rozkład jest skoncentrowany, a jeśli są daleko, jest to rozkład rozproszony.

Istnieje wiele miar zmienności, wśród najbardziej znanych jest:

  • Zakres
  • Średnie odchylenie
  • Zmienność
  • Odchylenie standardowe

Środki te uzupełniają środkowe miary tendencji i są niezbędne do zrozumienia rozkładu uzyskanych danych i wydobywania jak największej ilości informacji.

Zakres

Zakres lub trasa mierzy amplitudę zestawu danych. Aby określić jego wartość, stwierdzono różnicę między najwyższą wartością xMax i najmniejsza wartość xmin:

R = xMax - Xmin

Jeśli dane nie są luźne, ale zgrupowane według przedziału, wówczas zakres jest obliczany na podstawie różnicy między górną granicą ostatniego przedziału a dolną granicą pierwszego przedziału.

Kiedy zakres jest niewielką wartością, oznacza to, że wszystkie dane są całkiem blisko siebie, ale duży zakres wskazuje, że istnieje duża zmienność. Oczywiste jest, że oprócz górnej granicy i dolnej granicy danych, zakres nie uwzględnia wartości między nimi, więc nie jest wskazane użycie, gdy numer danych jest duży.

Obliczenie i ma te same jednostki danych, jest jednak natychmiastową miarą, więc łatwo ją zinterpretować.

Przykład rangi

Następnie lista jest dostępna z liczbą celów oznaczonych w weekend, w ligach piłkarskich z dziewięciu krajów:

Może ci służyć: jakie są dzielniki 30? (Wyjaśnienie)

40, 32, 35, 36, 37, 31, 37, 29, 39

Jest to zestaw danych bez grupowania. Aby znaleźć zasięg, zamawiają je od najmniej do największego:

29, 31, 32, 35, 36, 37, 37, 39, 40

Dane o najwyższej wartości to 40 celów, a ta o najniższej wartości to 29 celów, dlatego zakres to:

R = 40–29 = 11 celów.

Można uznać, że zakres jest niewielki w porównaniu z danymi o wartości minimalnej, czyli 29 celów, więc można założyć, że dane nie mają dużej zmienności.

Średnie odchylenie

Ta miara zmienności jest obliczana na podstawie średniej wartości bezwzględnych odchyleń w odniesieniu do średniej. Oznaczanie średniego odchylenia jako dM, W przypadku danych niezgrupowych średnie odchylenie jest obliczane według następującego wzoru:

Gdzie n jest liczbą dostępnych danych, xSiema Reprezentuje każde dane, a x̄ to średnia, która jest określana przez dodanie wszystkich danych i podzielenie między N:

Średnie odchylenie pozwala średnio wiedzieć, ile jednostek dane odbiegają od arytmetyki i mają tę zaletę, że posiadanie tych samych jednostek, co dane, z którymi działają.

Przykład odchylenia środkowego

Zgodnie z danymi z zakresu liczba oznaczonych celów wynosi:

40, 32, 35, 36, 37, 31, 37, 29, 39

Jeśli chcesz znaleźć średnie odchylenieM Spośród tych danych konieczne jest najpierw obliczenie średniej arytmetycznej X̄:

A teraz, gdy wartość X̄ jest znana, stwierdzamy średnie odchylenieM:

= 2.99 ≈ 3 bramki

Dlatego można powiedzieć, że średnio dane odsuwają się w przybliżeniu w 3 średnich celach, które są 35 celami, i jak wspomniano, jest to znacznie dokładniejsza miara niż zakres.

Może ci służyć: hiperbola

Zmienność

Średnie odchylenie jest znacznie cieńszą miarą zmienności niż zakres, ale jak obliczono na podstawie wartości bezwzględnej różnic między każdym daniem a średnią, nie oferuje większej wszechstronności z algebraicznego punktu widzenia.

Dlatego preferowana jest wariancja, która odpowiada średniej różnicy kwadratowej każdej danych ze średnią i jest obliczana przy użyciu wzoru:

W tym wyrażeniu S2 oznacza wariancję i jak zawsze xSiema Reprezentuje każdą z danych, x̄ to średnia i n całkowitych danych.

Podczas pracy z próbką zamiast populacji preferuje się obliczenie takiej wariancji:

Różnica w poprzednim wzorze polega na tym, że w mianowniku jest N - 1 zamiast n. Zdarza się, że dzieląc przez n, wariancja próbki nie docenia wariancji populacji, z której została wyodrębniona, ale nie wtedy, gdy jest dzielona przez n - 1. W niektórych tekstach, które wyrażenie pojawia się z nazwą Quasi-Variza.

W każdym razie wariancja charakteryzuje się zawsze ilością dodatnią, ale będąc średnią różnic kwadratowych, ważne jest, aby zauważyć, że nie ma takich samych jednostek, jak te z danych.

Przykład wariancji

Aby obliczyć wariancję danych przykładów zakresu i średniego odchylenia, odpowiednie wartości są zastąpione i wskazana suma. W takim przypadku jest wybrane do podzielenia między N-1:

= 13.86

Odchylenie standardowe

Wariancja nie ma takiej samej jednostki, jak w badanej zmiennej, na przykład, jeśli dane są dostarczane w licznikach, wariancja powoduje metry kwadratowe. Lub w przykładzie celów, które byłyby w celach kwadratowych, co nie ma sensu.

Może ci służyć: jakie są elementy przypowieści? (Części)

Dlatego definiuje się odchylenie standardowe, zwane również typowe odchylenie, Jak pierwiastek kwadratowy wariancji:

S = √s2

W ten sposób miara zmienności danych jest uzyskiwana w tych samych jednostkach, a im niższa wartość S, tym bardziej zgrupowane dane są wokół średniej.

Zarówno wariancja, jak i odchylenie standardowe są miarami zmienności, które należy wybrać, gdy średnia arytmetyczna jest miarą centralnej tendencji, która najlepiej opisuje zachowanie danych.

I jest tak, że odchylenie standardowe ma ważną własność, znaną jako twierdzenie Chebyheva: co najmniej 75% obserwacji jest w przedziale określonym przez X ± 2s. Innymi słowy, 75% danych jest co najwyżej w odległości równej 2s około średniej.

Podobnie, co najmniej 89% wartości znajduje się w odległości 3s od średniej, procent, który można rozszerzyć, pod warunkiem, że dostępnych jest wiele danych, a one są zgodne z rozkładem normalnym.

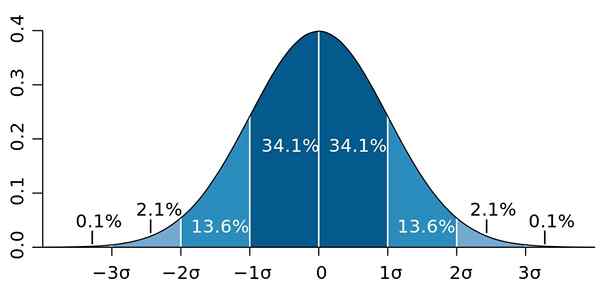
Rysunek 2.- Jeśli dane podążają za rozkładem normalnym, 95.4 z nich to dwa standardowe odchylenia po obu stronach średniej. Źródło: Wikimedia Commons.

Przykład odchylenia standardowego

Standardowe odchylenie danych przedstawionych w poprzednich przykładach to:

S = √s2 = √13.86 = 3.7 ≈ 4 bramki