Rozkład wykładniczy

Wyjaśniamy, co to jest rozkład wykładniczy, jego cechy, wzory, przykłady i rozwiązywane ćwiczenia

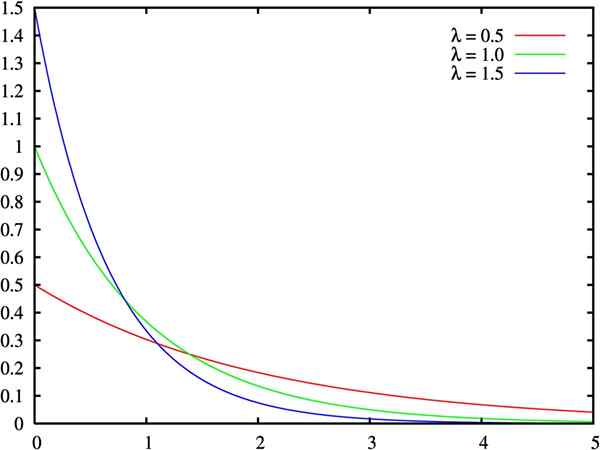
Wykres funkcji gęstości rozkładu wykładniczego, dla trzech wartości parametru Lambda. Źródło: Wikimedia Commons.

Co to jest rozkład wykładniczy?

Rozkład wykładniczy Jest to model probabilistyczny dla ciągłych zmiennych losowych. Oznacza to, że dzięki temu możesz znać prawdopodobieństwo wystąpienia pewnej wartości zmiennej, więc jest to rozkład prawdopodobieństwa.

Aby uzyskać rozkład, zaczyna się od funkcja gęstości, który ma wykładniczy kształt parametru λ> 0:

Funkcja gęstości jako taka nie pozwala na obliczenie prawdopodobieństwa, ale po ustaleniu f (x) funkcję rozkładu f (x), za pomocą której uzyskuje się prawdopodobieństwa, jest uzyskiwana przez integrację f (x). Na przykład prawdopodobieństwo P, że zmienna losowa przyjmuje wartości między 0 a x, wynosi:

Wykonanie integracji, która jest bardzo prosta, ponieważ całka wykładnicza jest ta sama wykładnicza, z wyjątkiem stałych towarzyszących argumentowi, jest uzyskiwana:

Rozkład wykładniczy jest szeroko stosowany do określenia prawdopodobieństwa zdarzenia po określonym czasie oczekiwania, na przykład czas, który ma miejsce w pojawieniu się szpitala, zanim przybył pacjent.

Często zdarzenia odnoszą się do awarii lub rozpadu typów elektrycznych, elektronicznych i innych. W takim przypadku rozkład wykładniczy pomaga oszacować czas potrzebny na awarię komponentu, a także czas między naprawami. Jest to znane jako teoria niezawodności.

Charakterystyka rozkładu wykładniczego

Niektóre z najwybitniejszych cech funkcji gęstości f (x) rozkładu wykładniczego są następujące:

• f (x) jest dodatni.
• Obszar pod krzywą y = f (x) = λe^−λX Jest zawsze równy 1, ponieważ suma prawdopodobieństwa wystąpienia wszystkich wartości zmiennej musi wynosić 1. Jest to warunek, który spełnia funkcje gęstości. Obszar ten jest obliczany za pośrednictwem całki:

Może ci służyć: anuma

Brak wykładniczej pamięci rozkładu

Najwybitniejszą cechą rozkładu wykładniczego jest brak pamięci. Załóżmy na przykład, że upłynął czas modelowanie z tym rozkładem, dopóki nie nastąpi awaria elementu.

Cóż, brak pamięci odnosi się do wiedzy, że element działał przez czas przeżycia „S”, nie modyfikuje prawdopodobieństwa, że ​​element będzie nadal biegał do określonego dodatkowego czasu „t”.

Oznacza to, że prawdopodobieństwo, że element zawodzi stąd do określonego czasu (na przykład 1 minuta, 1 godzina) nie zależy od tego, że działało dobrze, że działało dobrze.

Matematycznie oblicza się z definicji prawdopodobieństwa niezależnych zdarzeń:

Dlatego prawdopodobieństwo nie zależy od S ani czasu przeżycia.

Formuły

1.- Funkcja gęstości rozkładu wykładniczego wynosi:

Gdzie λ jest parametrem rozkładu.

2.- Jak opisano powyżej, rozkład samego prawdopodobieństwa jest oznaczony jako F (x), a różne prawdopodobieństwa uzyskuje się przez integrację funkcji gęstości:

3.- Z powyższego wynika, że ​​prawdopodobieństwo, że zmienna przyjmuje wartości mniejsze lub równe „x” wynosi p [x ≤x] = 1 −e^−λX.

4.- Obszar pod krzywą y = f (x), uwzględniony między a i b, pozwala obliczyć prawdopodobieństwo, że zmienna jest w przedziale [a, b]. Ten obszar to:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- Wartość p [x ≥ a] wynosi 1 - f (a) = 1 - (1 - e^−λX) = e^−λX

Oczekiwana wartość rozkładu wykładniczego

Nadzieja lub oczekiwana wartość e (x) rozkładu wykładniczego jest wartością, która ma się występować częściej. Jest obliczany na podstawie całki:

Może Ci służyć: techniki rejestracji informacji

Co jest łatwo rozwiązane metodą integracji przez części. Wynik to:

E (x) = 1/λ

Wariancja rozkładu wykładniczego

Do obliczenia wariancji należy określić całkę:

Który jest również rozwiązany za pomocą metody integracji przez części, aby uzyskać:

Var (x) = 1/λ²

Szczególność rozkładu wykładniczego jest to, że odchylenie standardowe S (x), zdefiniowane jako pierwiastek kwadratowy wariancji to:

S (x) = √var (x) = √ (1/λ²) = 1/λ

Oznacza to, że odchylenie standardowe jest równe nadziei na dystrybucję.

Przykłady rozkładu wykładniczego

Datowanie próbek węgla 14

Rozkład wykładniczy służy do określenia czasu potrzebnego do rozpadu cząstki radioaktywnej. Te czasy są używane do datowania próbek kopalnych przez radiowęglowy.

Czas potrzebny na sprawdzenie poczty

Możesz modelować czas, który użytkownicy zajmują na przejrzenie ich e -maila, po otrzymaniu powiadomienia za pomocą dystrybucji wykładniczej. Załóżmy, że parametr rozkładu wynosi λ = 0.2 Zatem prawdopodobieństwo, że dana osoba zajmuje mniej niż 1 minutę, aby przejrzeć swoją e -mail:

Ta całka została rozwiązana na początku, pozostaje tylko na zastąpienie wartości numerycznych w roztworze i obliczenie końcowego wyniku:

P [x ≤ 1] = 1 --e^-0.2×1 = 1− e^-0.2 = 1– 0.819 = 0.181

Można go również bezpośrednio wymienić na funkcji F (x) podanej powyżej, aby uzyskać F (1).

Ćwiczenia

Ćwiczenie 1

Znajdź prawdopodobieństwo, że osoba później jedna godzina przeglądała e -mail, jeśli rozkład prawdopodobieństwa jest wykładniczy, z parametrem λ = 0.2.

Rozwiązanie

P [x ≥ 60] należy obliczyć, ponieważ 1 godzina jest równoważna 60 minut i prawdopodobieństwa, że ​​osoba pod koniec 60 minut lub więcej na sprawdzenie poczty jest wymagane. Prawdopodobieństwo oblicza się z tą samą całką przedstawioną na początku, po prostu zmieniając granice integracji:

Może ci służyć: Rapa Nui: historia, cechy, kultura, tradycje

Uzyskana wartość jest niewielka, więc jest bardzo mało prawdopodobne, aby osoba zajmowała ponad godzinę na przejrzenie e -maila.

Ćwiczenie 2

Żarówki elektryczne zwykle mają skończony czas, z wyjątkiem słynnej żarówki straży pożarnej w Livermore w Kalifornii, która nigdy nie zawiodła od pierwszego razu, w 1901 roku.

Załóżmy, że czas trwania bieżącej żarówki wynika z rozkładu wykładniczego, z oczekiwaną wartością 8 miesięcy. Oblicz:

a) Jakie jest prawdopodobieństwo, że żarówka będzie trwać od 5 do 14 miesięcy?

b) prawdopodobieństwo, że żarówka będzie trwać ponad 25 miesięcy, wiedząc, że ma ponad 11 miesięcy.

Rozwiązanie

Pierwszą rzeczą jest znalezienie wartości λ, poprzez oczekiwaną wartość rozkładu e (x) = 8 miesięcy. Zgodnie z tym, co zostało powiedziane w poprzednim rozdziale, oczekiwana wartość jest odwrotność parametru λ, dlatego:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Następnie obliczane jest wymagane prawdopodobieństwo, za pomocą całki podanej na początku, ale wygodnie zmieniają granice integracji:

Następnie jest zastępowany w funkcji F (x) podanej w poprzedniej sekcji, jak następuje:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Rozwiązanie b

Aby odpowiedzieć na ten problem, zostanie użyta właściwość braku pamięci, wypowiedziana powyżej. Jak wiadomo, że trwał już ponad 11 miesięcy, zatem:

S = 11 miesięcy

Dodatkowy czas do trwania 25 miesięcy lub więcej to:

T = 14 miesięcy

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{−0.125 × 14} = 0.174