Formuły rozkładu Poissona, równania, model, właściwości

Dystrybucja Poissona Jest to dyskretny rozkład prawdopodobieństwa, za pomocą którego można znać prawdopodobieństwo, że w dużej próbce i podczas pewnego przedziału występuje zdarzenie, którego prawdopodobieństwo jest niewielkie.

Często można zastosować rozkład Poissona zamiast rozkładu dwumianowego, o ile opisano następujące warunki: duża próbka i małe prawdopodobieństwo.

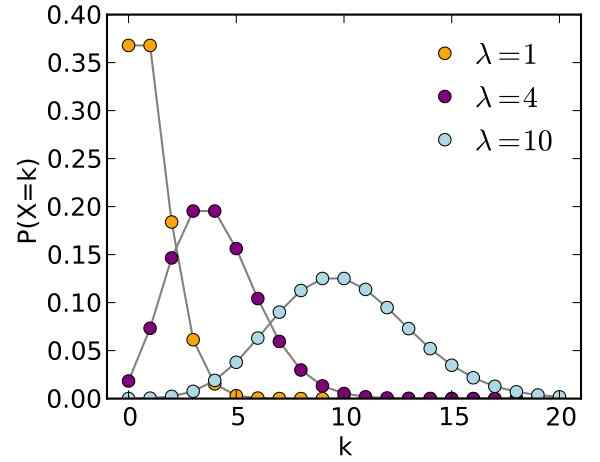
Rysunek 1. Wykres rozkładu Poissona dla różnych parametrów. Źródło: Wikimedia Commons.

Siméon-Denis Poisson (1781–1840) stworzył ten rozkład, który nosi jego imię, bardzo przydatne, jeśli chodzi o nieprzewidywalne wydarzenia. Poisson opublikował swoje wyniki w 1837 r., Prace badawcze dotyczące prawdopodobieństwa wystąpienia błędnych wyroków karnych.

Następnie inni badacze dostosowali dystrybucję w innych obszarach, na przykład liczba gwiazd, które mogłyby znajdować się w określonej objętości przestrzeni lub prawdopodobieństwa umrze żołnierza z powodu konia Coz.

[TOC]

Wzór i równania

Matematyczna forma dystrybucji Poissona jest następująca:

 - Zmienna losowa jest I

- μ (czasami również oznaczane jako λ) Jest to średni lub parametr rozkładu

- Numer Eulera: E = 2.71828

- Prawdopodobieństwo uzyskania y = k wynosi p

- k Jest to liczba sukcesów 0, 1,2,3 ..

- N Jest to liczba testów lub zdarzeń (wielkość próbki)

Odrębne zmienne losowe, jak sama nazwa wskazuje, zależą od przypadków i przyjmują tylko dyskretne wartości: 0, 1, 2, 3, 4 ..., k.

Średnia rozkładu jest podana przez:

Wariancja σ, która mierzy dyspersję danych, jest kolejnym ważnym parametrem. Dla dystrybucji Poissona jest to:

σ = μ

Poisson ustalił, że gdy n → ∞ i p → 0, średnia μ -nazywana również wartość oczekiwana- Ma tendencję do stałej:

μ → stałe

Ważny: P Jest to prawdopodobieństwo wystąpienia zdarzenia uwzględniającego całkowitą populację, podczas gdy P (y) To prognoza Poissona na temat próbki.

Model i właściwości

Rozkład Poissona ma następujące właściwości:

-Rozmiar próbki jest duży: N → ∞.

-Rozważane zdarzenia lub zdarzenia są niezależne od siebie i występują losowo.

-Prawdopodobieństwo P Co za pewne wydarzenie I Występuje przez określony czas jest bardzo mały: P → 0.

-Prawdopodobieństwo więcej niż jednego zdarzenia w przedziale czasu wynosi 0.

-Średnia wartość jest zbliżona do stałej podanej przez: μ = n.P (n to wielkość próbki)

-Ponieważ dyspersja σ jest równa μ, ponieważ przyjmuje większe wartości, zmienność jest również większa.

-Zdarzenia muszą być dystrybuowane równomiernie w stosowanym przedziale czasowym.

-Zestaw możliwych wartości zdarzeń I To jest: 0,1,2,3,4 .. .

Może ci służyć: losowy eksperyment: koncepcja, przestrzeń próbki, przykłady

-Suma Siema Zmienne, które po rozkładu Poissona są również kolejną zmienną Poissona. Jego średnia wartość jest sumą średnich wartości tych zmiennych.

Różnice z rozkładem dwumianowym

Rozkład Poissona różni się od rozmieszczenia dwumianowego w następujących ważnych aspektach:

-Na rozkład dwumianowy wpływa zarówno wielkość próbki S, jak i prawdopodobieństwo P, Ale rozkład Poissona wpływa jedynie średnia μ.

-W rozkładu dwumianowym możliwe wartości zmiennej losowej I Wynoszą 0,1,2,… zamiast tego w rozmieszczeniu Poissona nie ma górnej granicy dla tych wartości.

Przykłady

Poisson początkowo zastosował swój słynny rozkład w sprawach prawnych, ale na poziomie przemysłowym jednym z jego pierwszych zastosowań było produkcja piwa. W tym procesie uprawy drożdży są używane do fermentacji.

Drożdże składa się z żywych komórek, których populacja jest zmienna w czasie. W produkcji piwa konieczne jest dodanie niezbędnej ilości, więc konieczne jest znanie ilości komórek na jednostkę objętości.

Podczas II wojny światowej dystrybucja Poissona była używana, aby wiedzieć, czy Niemcy naprawdę wskazują na Londyn z Calais, czy po prostu strzelali losowo. Było to ważne dla aliantów, aby ustalić, jak dobra była technologia dostępna dla nazistów.

Praktyczne zastosowania

Aplikacje dystrybucyjne Poissona zawsze odnoszą się do liczby czasów lub liczby przestrzeni. A ponieważ prawdopodobieństwo wystąpienia jest niewielkie, jest również znane jako „prawo rzadkich wydarzeń”.

Oto lista wydarzeń, które należą do jednej z tych kategorii:

-Rejestracja cząstek w rozkładu radioaktywnym, podobnie jak wzrost komórek drożdży, jest funkcją wykładniczą.

-Liczba wizyt na określonej stronie internetowej.

-Przybycie ludzi do rządu, aby zapłacić lub uczestniczyć (teoria ogonów).

-Liczba samochodów, które przechodzą przez określony punkt na drodze, przez dany czas czasowy.

Rysunek 2. Ilość samochodów, które przechodzą przez punkt, jest w przybliżeniu rozkładem Poissona. Źródło: Pixabay.

-Mutacje cierpiały w pewnym łańcuchu DNA po otrzymaniu narażenia na promieniowanie.

-Liczba meteorów średnicy większa niż 1 m spadła w ciągu roku.

-Wady na metr kwadratowy tkaniny.

-Ilość komórek krwi w 1 centymetrze sześciennym.

-Połączenia na minutę do wymiany telefonicznej.

-Iskry czekoladowe obecne w 1 kg ciasta ciasta.

-Liczba drzew zarażonych na drodze 1 hektara lasu.

Należy zauważyć, że te zmienne losowe reprezentują liczbę zdarzeń zdarzenia przez stały czas (Połączenia na minutę do wymiany telefonicznej) lub dany region przestrzeni (Wady tkaniny na metr kwadratowy).

Może ci służyć: proporcjonalna różnica

Wydarzenia te, jak już ustalone, są niezależne od czasu, który minął od ostatniego wydarzenia.

Zbliżając się do rozmieszczenia dwumianowego z rozkładem Poissona

Rozkład Poissona jest dobrym podejściem do rozmieszczenia dwumianowego, o ile:

-Rozmiar próbki jest duży: n ≥ 100

-Prawdopodobieństwo P jest mały: p ≤ 0,1

- μ być w kolejności: NP ≤ 10

W takich przypadkach dystrybucja Poissona jest doskonałym narzędziem, ponieważ rozkład dwumianowy może stać się skomplikowany w tych przypadkach.

Rozwiązane ćwiczenia

Ćwiczenie 1

Badanie sejsmologiczne wykazało, że w ciągu ostatnich 100 lat na całym świecie było 93 duże trzęsienia ziemi, co najmniej 6.0 w skali Richter -logarithmic-. Załóżmy, że rozkład Poissona jest w tym przypadku odpowiednim modelem. Znajdować:

a) Średnie występowanie dużych trzęsień ziemi rocznie.

b) Tak P (y) Jest to prawdopodobieństwo wydarzenia I Trzęsienia ziemi na losowy wybrany rok, znajdź następujące prawdopodobieństwa:

P(0), P(1), P (2), P (3), P (4), P (5), P (6) i P (7).

c) Prawdziwe wyniki badania są następujące:

- 47 lat (0 trzęsień ziemi)

- 31 lat (1 trzęsienia ziemi)

- 13 lat (2 trzęsienia ziemi)

- 5 lat (3 trzęsienia ziemi)

- 2 lata (4 trzęsienia ziemi)

-  0 lat (5 trzęsień ziemi)

- 1 lata (6 trzęsień ziemi)

- 1 lata (7 trzęsień ziemi)

Jak te wyniki z wynikami uzyskanymi w podsekcji B? Czy dystrybucja Poissona jest dobrym wyborem do modelowania tych zdarzeń?

Rozwiązanie)

a) Trzęsienia ziemi to zdarzenia, których prawdopodobieństwo P Jest mały i rozważamy ograniczony czas, jeden rok. Przeciętne trzęsienia ziemi to:

μ = 93/100 trzęsienia ziemi / rok = 0.93 trzęsienia ziemi rocznie.

Rozwiązanie B)

b) Aby obliczyć żądane prawdopodobieństwa, wartości są zastępowane w wzorze podanym na początku:

Na przykład P (2), To byłoby prawdopodobieństwo, że rocznie będą 2 duże trzęsienia ziemi:

y = 2

μ = 0.93

E = 2.71828

I to jest prawdopodobieństwo, że na rok jest 7 dużych trzęsień ziemi:

Jest to całkiem mniej niż p (2).

Wyniki są wymienione poniżej:

P (0) = 0.395, p (1) = 0.367, p (2) = 0.171, p (3) = 0.0529, P (4) = 0.0123, p (5) = 0.00229, p (6) = 0.000355, p (7) = 0.0000471.

Na przykład możemy powiedzieć, że istnieje prawdopodobieństwo 39.5 %, że w danym roku nie występuje wielkie trzęsienie ziemi. Lub że istnieje 5,29 %, że w tym roku występuje 3 duże trzęsienia ziemi.

Rozwiązanie C)

c) Częstotliwości są analizowane, mnożąc się przez n = 100 lat:

39.5; 36.7; 17.1; 5.29; 1.23; 0.229; 0.0355 i 0.00471.

Może ci służyć: pochodne algebraiczne

Na przykład:

- Częstotliwość 39.5 wskazuje, że w 39.5 ze 100 lat lub dużych trzęsień ziemi, moglibyśmy powiedzieć, że jest to całkiem blisko prawdziwego 47 -latku -wolny wynik bez żadnego wielkiego trzęsienia ziemi.

Porównajmy kolejny wynik Poissona z prawdziwymi wynikami:

- Wartość uzyskana z 36.7 oznacza, że ​​w okresie 37 lat jest 1 wielkie trzęsienie ziemi. Prawdziwy wynik jest taki, że za 31 lat było 1 wielkie trzęsienie ziemi, dobry zbieg okoliczności z modelem.

- 17 jest oczekiwane.1 lata z 2 dużymi trzęsieniami ziemi i wiadomo, że za 13 lat, co jest bliską wartością, w efekcie istniało 2 duże trzęsienia ziemi.

Dlatego model Poissona jest dopuszczalny w tym przypadku.

Ćwiczenie 2

Firma szacuje, że liczba komponentów, które zawodzą przed ukończeniem 100 godzin pracy, jest zgodna z dystrybucją Poissona. Jeśli średnia liczba awarii wynosi 8 w tym czasie, znajdź następujące prawdopodobieństwa:

a) że komponent zawodzi w ciągu 25 godzin.

b) awaria mniej niż dwa elementy, w 50 godzin.

c) że co najmniej trzy komponenty zawodzą w ciągu 125 godzin.

Rozwiązanie)

a) Wiadomo, że średnia błąd w 100 godzinach wynosi 8, dlatego w 25 godzinach czwartej części awarii jest oczekiwana, to znaczy 2 niepowodzenia. To będzie parametr μ.

Żądane jest prawdopodobieństwo awarii 1 komponentu, losową zmienną jest „składniki, które zawodzą przed 25 godzinami”, a jej wartość wynosi y = 1. Zastępując funkcję prawdopodobieństwa:

 b) Teraz losową zmienną jest „składniki, które zawodzą przed 50 godzinami”. Parametr to μ = 4, Ponieważ oczekiwana wartość awarii w 50 godzinach wynosi 4.

Pytanie polega jednak na prawdopodobieństwie, że mniej niż dwa elementy zawodzą w ciągu 50 godzin, nie że dokładnie 2 komponenty zawodzą w ciągu 50 godzin, dlatego musimy dodać prawdopodobieństwo, że:

-Żaden nie zawiedzie

-PRACA TYLKO 1

P (mniej niż 2 składniki) = P (0) + P (1)

P (mniej niż 2 komponenty) = 0.0183+0.0732 = 0.0915

c) że co najmniej 3 komponenty zawodzą w 125, oznacza to, że 3, 4, 5 lub więcej w tym czasie może się nie udać.

Prawdopodobieństwo, które wystąpi przynajmniej jedno z kilku zdarzeń, jest równe 1, z wyjątkiem prawdopodobieństwa, że ​​żadne z zdarzeń się nie wydarzy.

-Wydarzenie, które jest poszukiwane, to porażka 3 lub więcej komponentów w 125 godzin

-To, że zdarzenie się nie zdarza, oznacza, że ​​mniej niż 3 komponenty zawodzą, których prawdopodobieństwo jest: P (0)+P (1)+P (2)

Parametr μ rozkładu w tym przypadku to:

 μ = 8 + 2 = 10 awarii w ciągu 125 godzin.

P (upadły 3 lub więcej składników) = 1- p (0)- p (1)- p (2) =

= 1-0.0026786 = 0.9972

Bibliografia

1. Mathworks. Dystrybucja Poissona. Odzyskane z: jest.Mathworks.com
2. Mendenhall, w. 1981. Statystyka administracji i ekonomii. 3. wydanie. Grupa redakcyjna Iberoamerica.
3. Stat Trek. Naucz się statystyki. Dystrybucja Poissona. Odzyskane z: Stattrek.com,
4. TRIOLA, m. 2012. Statystyka podstawowa. 11. Wyd. Edukacja Pearsona.
5. Wikipedia. Dystrybucja Poissona. Źródło: w:.Wikipedia.org