Formuły współczynników korelacji, obliczenia, interpretacja, przykład

On Współczynnik korelacji W statystykach jest to wskaźnik, że mierzy trend dwóch zmiennych ilościowych x i y, aby mieć związek liniowości lub proporcjonalności między nimi.

Zasadniczo pary zmiennych x i y są dwiema cechami tej samej populacji. Na przykład x może być wysokością osoby e i jej wagi.

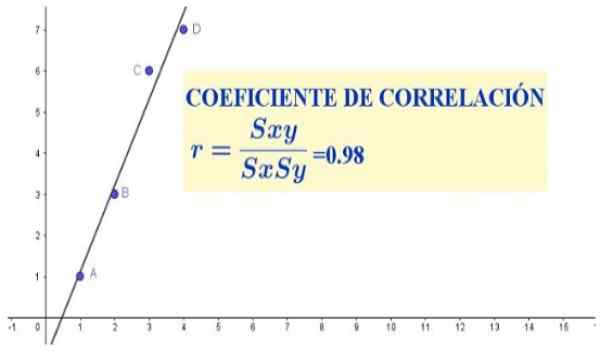
Rysunek 1. Współczynnik korelacji dla czterech par danych (x, y). Źródło: f. Zapata.

W tym przypadku współczynnik korelacji wskazywałby, czy istnieje stosunek proporcjonalności między wysokością a wagą danej populacji.

Liniowy współczynnik korelacji Pearsona jest oznaczony listem R małe litery i jego minimalne i maksymalne wartości wynoszą odpowiednio -1 i +1. 

Wartość r = +1 wskazałaby, że całe pary (x, y) są doskonale wyrównane i że gdy x rośnie i będzie rosła w tej samej proporcji. Z drugiej strony, jeśli zdarzy się, że r = -1, zestaw par byłby również doskonale wyrównany, ale w takim przypadku, gdy X rośnie i zmniejsza się w tej samej proporcji.

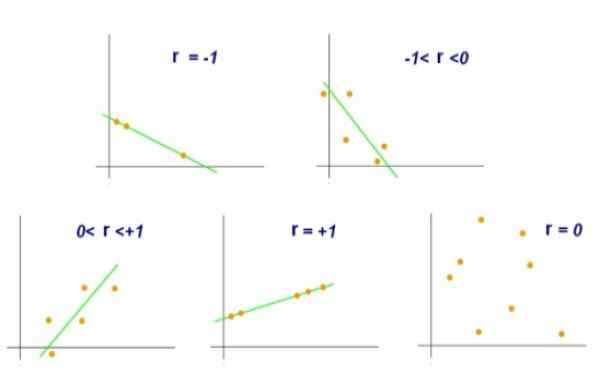Rysunek 2. Różne wartości współczynnika korelacji liniowej. Źródło: Wikimedia Commons.

Z drugiej strony wartość r = 0 wskazałaby, że nie ma liniowej korelacji między zmiennymi x i y. Podczas gdy wartość r = +0,8 wskazywałaby, że pary (x, y) mają tendencję do grupowania na jedną stronę i drugiej określonej linii.

Wzór obliczania współczynnika korelacji R jest następujący:

Gdzie licznik reprezentuje kowariancję między zmiennymi X i.

Jak obliczyć współczynnik korelacji?

Współczynnik korelacji liniowej to kwota statystyczna, która jest włączona do kalkulatorów naukowych, w większości arkuszy kalkulacyjnych i programach statystycznych.

Może ci służyć: hiperboliczny paraboloid: definicja, właściwości i przykłady

Jednak wygodnie jest wiedzieć, w jaki sposób formuła, która ją definiuje, jest zastosowana, a dla tego zostanie wyświetlona szczegółowe obliczenia, przeprowadzone na małym zestawie danych.

I jak stwierdzono w poprzednim rozdziale, współczynnikiem korelacji jest kowariancja SXY podzielona przez iloczyn odchylenia standardowego SX dla zmiennych x i SY dla zmiennej i.

Kowariancja i wariancja

Kowariancja SXY to:

Sxy = [σ (xi -) (yi -)] / (n -1)

Gdzie suma przechodzi od 1 do n par (xi, yi). E są arytmetycznymi pończochami odpowiednio danych xi e yi.

Ze swojej części odchyleniem standardowym dla zmiennej x jest pierwiastkiem kwadratowym wariancji zestawu danych XI, z I od 1 do N:

Sx = √ [σ (xi -)^2) / (n -1)]

Podobnie, odchylenie standardowe dla zmiennej i jest pierwiastkiem kwadratowym wariancji zestawu danych Yi, z I od 1 do N:

Sy = √ [σ (yi -)² ) / (N-1)]

Przypadek ilustracyjny

Aby szczegółowo pokazać sposób obliczenia współczynnika korelacji, weźmiemy następujący zestaw czterech par danych 

(X, y): (1, 1); (23); (3, 6) i (4, 7).

Najpierw obliczamy średnią arytmetyczną dla x i y, jak następuje:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Następnie obliczane są pozostałe parametry:

Sxy kowariancja

Sxy = [(1 - 2.5) (1–4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Może ci służyć: zasady pochodzenia (z przykładami)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Odchylenie standardowe SX

Sx = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Odchylenie standardowe SY

Sx = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Współczynnik poręczy r

R = 3.5 / (1.29 * 2.75) = 0.98

Interpretacja

W zestawie danych w poprzednim przypadku istnieje silna liniowa korelacja między zmiennymi x i y, która objawia się zarówno na wykresie dyspersyjnym (które można zobaczyć na rycinie 1), jak i w współczynniku korelacji, który rzucił wartość dość zbliżoną do jednostka.

W zakresie, w jakim współczynnik korelacji jest bliżej 1 lub -1, bardziej sensowne jest ustawienie danych do linii, wynik regresji liniowej.

Regresja liniowa

Linia regresji liniowej jest uzyskiwana z Metoda najmniejszych kwadratów. w którym parametr linii regresji jest uzyskiwany z minimalizacji sumy kwadratu różnicy między wartością a oszacowaną a yi danych n.

Z drugiej strony parametry a i b linii regresji y = a + bx, uzyskane metodą minimalnych kwadratów, to:

*B = sxy / (sx²) Dla zbocza

*A = - b dla przecięcia linii regresji z osą i.

Przypomnijmy, że SXY jest kowariancją zdefiniowaną powyżej i SX² Jest to wariancja lub kwadrat odchylenia standardowego wcześniej zdefiniowanego. E są arytmetycznymi środkami danych x i odpowiednio.

Przykład

Współczynnik korelacji służy do ustalenia, czy istnieje korelacja typu liniowego między dwiema zmiennymi. Ma zastosowanie, gdy zbadanie zmiennych są ilościowe, a także powinny być zgodne z normalnym rozkładem typu.

Może ci służyć: reguła korespondencji funkcji

Ilustracyjnym przykładem, który mamy poniżej: Miarą stopnia otyłości jest wskaźnik masy ciała, który jest uzyskiwany przez podzielenie ciężaru jednej osoby na kilogramy między wysokością tego samego w jednostkach kwadratowych na kwadrat.

Pożądane jest, aby wiedzieć, czy istnieje silna korelacja między wskaźnikiem masy ciała a stężeniem cholesterolu HDL we krwi, mierzonej w milimole na litr. W tym celu przeprowadzono badanie z 533 osobami podsumowanymi na poniższym wykresie, na którym każdy punkt reprezentuje dane osoby.

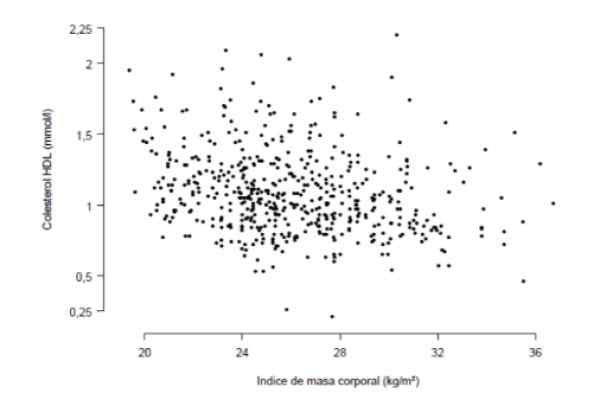Rysunek 3. Badanie IMC i cholesterol HDL u 533 pacjentów. Źródło: Aragonese Institute of Health Sciences (IACS).

Z dokładnej obserwacji wykresu wynika z tego, że istnieje pewien (niezbyt wyraźny) trend między stężeniem cholesterolu HDL a wskaźnikiem masy ciała. Miarem ilościową tego trendu jest współczynnik korelacji, który w tym przypadku okazał się r = -0,276.

Bibliografia

1. González c. Statystyka ogólna. Odzyskane z: tarwi.La Molina.Edu.pe
2. IAC. Aragonese Institute of Health Sciences. Pobrano z: ICS-Aragon.com 
3. Salazar c. i Castillo s. Podstawowe zasady statystyki. (2018). Źródło: DSPACE.Uce.Edu.Ec
4. Superprof. Współczynnik korelacji. Odzyskane z: Superprof.Jest
5. USAC. Podręcznik statystyki opisowej. (2011). Odzyskane z: statystyki.Inżynieria.USAC.Edu.Gt
6. Wikipedia. Współczynnik korelacji Pearsona. Odzyskane z: jest.Wikipedia.com.