Liniowe rozszerzenie Czym jest, wzór i współczynniki, przykład

Liniowe rozszerzenie występuje, gdy obiekt doświadcza rozszerzenia z powodu zmienności temperatury, głównie w jednym wymiarze. Wynika to z charakterystyk materiału lub jego geometrycznego kształtu. 

Na przykład w drucie lub w pasku, gdy wzrost temperatury jest długa, która cierpi na największą zmianę z powodu rozszerzenia termicznego.

Ptaki pozowane w przewodach. Źródło: Pixabay.

Kable, w których ptaki z poprzedniej figury cierpią, gdy wzrasta ich temperatura; Zamiast tego kurczą się, kiedy się chłodzi. W ten sam sposób, w jaki to się dzieje, z prętami tworzącymi szyny kolei.

[TOC]

Co to jest liniowe rozszerzenie?

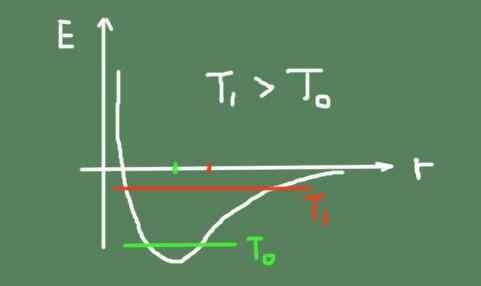Wykres energii wiązania chemicznego w porównaniu z odległością międzyatomową. Źródło: Self Made.

W stałym materiale atomy utrzymują swoje względne pozycje mniej więcej ustalone wokół punktu równowagi. Jednak ze względu na pobudzenie termiczne zawsze otaczają wokół niego.

Poprzez zwiększenie temperatury wzrasta również oscylacja termiczna, powodując zmianę pozycji oscylacji średniej. Wynika to z faktu, że potencjał łącza nie jest dokładnie paraboliczny i ma asymetrię wokół minimum.

Poniżej znajduje się liczba, która przedstawia energię wiązania chemicznego w zależności od odległości międzyatomicznej. Pokazano również całkowitą energię oscylacji w dwóch temperaturach i sposób poruszania się centrum oscylacji.

Wzór rozszerzenia liniowego i jego współczynnik

Aby zmierzyć rozszerzenie liniowe, zaczynamy od początkowej długości LE i początkowej temperatury t, od obiektu, którego chcesz zmierzyć rozszerzenie.

Załóżmy, że ten obiekt jest paskiem, którego długość wynosi l, a wymiary przekroju są znacznie niższe niż L.

Może ci służyć: natychmiastowe przyspieszenie: co to jest, jak jest obliczane i ćwiczenia

Po pierwsze, obiekt ten jest poddawany zmianom temperatury δT, tak że końcowa temperatura obiektu po ustaleniu równowagi ciepła ze źródłem ciepła wynosił.

Podczas tego procesu długość obiektu zmieni się również na nową wartość l '= l + δl, gdzie δL jest zmiennością długości.

Liniowy współczynnik rozszerzenia α jest zdefiniowany jako stosunek między względną zmiennością długości na jednostkę zmienności temperatury. Poniższy wzór określa liniowy współczynnik rozszerzenia α:

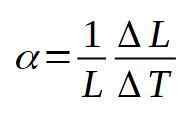W większości przypadków, α Ma stałą wartość dla temperatur między (t - δT) i (t + δt).

Wymiary liniowego współczynnika rozszerzenia to wymiary temperatury.

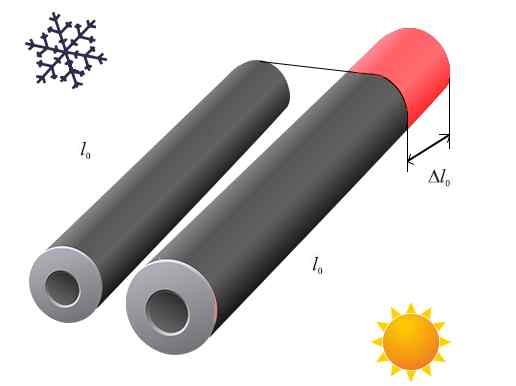
Temperatura zwiększa długość stałych w kształcie rurki. To jest znane jako rozszerzenie liniowe. Źródło: Lafer.com

Liniowy współczynnik rozszerzenia dla różnych materiałów

Następnie podamy listę liniowego współczynnika rozszerzenia dla niektórych typowych materiałów i elementów. Współczynnik oblicza się w normalnym ciśnieniu atmosferycznym na podstawie temperatury otoczenia 25 ° C; a jego wartość jest uważana za stały w zakresie δT do 100 ° C.

Liniowa jednostka współczynnika rozszerzenia będzie (° C)^-1.

- Stal: α = 12 ∙ 10^-6 (° C)^-1

- Aluminium: α = 23 ∙ 10^-6 (° C)^-1

- Złoto: α = 14 ∙ 10^-6 (° C)^-1

- Miedź: α = 17 ∙ 10^-6 (° C)^-1

- Mosiądz: α = 18 ∙ 10^-6 (° C)^-1

- Żelazo: α = 12 ∙ 10^-6 (° C)^-1

- Szkło: α = (7 do 9) ∙ 10^-6 (° C)^-1

- Rtęć: α = 60,4 ∙ 10^-6 (° C)^-1

- Kwarc: α = 0,4 ∙ 10^-6 (° C)^-1

- Diament: α = 1,2 ∙ 10^-6 (° C)^-1

- Ołów: α = 30 ∙ 10^-6 (° C)^-1

Może ci służyć: konwekcyjna transfer ciepła (z przykładami)

- Drewno dębowe: α = 54 ∙ 10^-6 (° C)^-1

- PVC: α = 52 ∙ 10^-6 (° C)^-1

- Włókno węglowe: α = -0.8 ∙ 10^-6 (° C)^-1

- Beton: α = (8 do 12) ∙ 10^-6 (° C)^-1

Większość materiałów rozciąga się ze wzrostem temperatury. Jednak niektóre specjalne materiały, takie jak włókno węglowe, wraz ze wzrostem temperatury.

Rozwiązane przykłady rozszerzenia liniowego

Przykład 1

Kabel miedziany jest zawieszony między dwoma słupkami, a jego długość w chłodnym dniu w 20 ° C wynosi 12 m. Oblicz wartość jej długości w upalny dzień w 35 ° C.

Rozwiązanie

Zaczynając od definicji liniowego współczynnika rozszerzenia i wiedząc, że dla miedzi ten współczynnik jest wart: α = 17 ∙ 10^-6 (° C)^-1

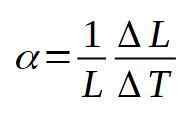
Wzrost długości jest podany przez: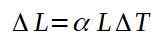

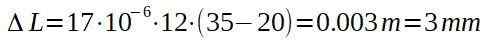
Kabel miedziany przechodzi wzrost swojej długości, ale jest to zaledwie 3 mm. To znaczy, że kabel przechodzi z 12 000 m na 12,003 m.

Przykład 2

W kowalstwie aluminiowy pręt pozostawia piekarnik w temperaturze 800 stopni Celsjusza, mierząc długość 10,00 m. Gdy ostygnie do temperatury otoczenia 18 stopni Celsjusza, określ długość, jaką będzie miał pasek.

Rozwiązanie

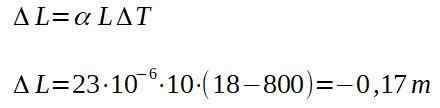
To znaczy, że bar, kiedyś zimno, będzie miał całkowitą długość:

9,83 m.

Przykład 3

Nit stalowy ma średnicę 0.915 cm. Otwór 0,910 cm jest wytwarzany na płycie aluminiowej. To jest początkowe średnice, gdy temperatura otoczenia wynosi 18 ° C.

W jakiej minimalnej temperaturze należy podgrzać płytkę, aby nit przeszedł przez otwór? Celem tego jest to, że gdy żelazo powraca do temperatury pokojowej, nit jest regulowany na płycie.

Może Ci służyć: Metoda równoległobramowa: przykłady, rozwiązane ćwiczenia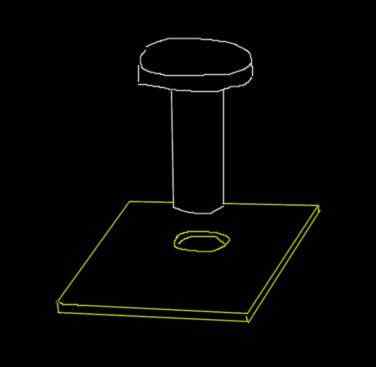Rysunek na przykład 3. Źródło: Self Made.

Rozwiązanie

Chociaż płyta jest obszarem, jesteśmy zainteresowani rozszerzeniem średnicy otworu, która jest ilością jednego wymiaru.

Zadzwońmy D₀ do pierwotnej średnicy płyty aluminiowej, a D, która będzie się ogrzewać.

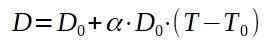
Oczyszczając końcową temperaturę t, masz:

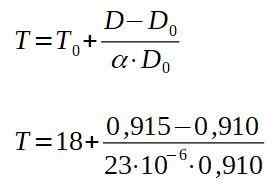
Wynik poprzednich operacji wynosi 257 ° C, czyli minimalną temperaturę, w której płyta musi być podgrzewana, aby nit przeszedł przez otwór.

Przykład 4

Nit i tablica poprzedniego ćwiczenia są umieszczane razem w piekarniku. Określ, jaka minimalna temperatura musi być piekarnik, aby nit stalowy przeszedł przez otwór płyty aluminiowej.

Rozwiązanie

W takim przypadku zarówno nit, jak i dziura opóźnią. Ale stalowy współczynnik rozszerzenia wynosi α = 12 ∙ 10^-6 (° C)^-1, Podczas gdy aluminium wynosi α = 23 ∙ 10^-6 (° C)^-1 .

Następnie szukamy końcowej temperatury T tak, że obie średnice się pokrywają.

Jeśli wezwamy 1 do nitu i 2 do płytki aluminiowej, szukamy końcowej temperatury t tak, jak d₁ = D₂.

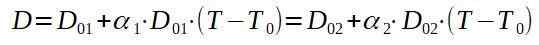
Jeśli wyczyścimy końcową temperaturę T, mamy:

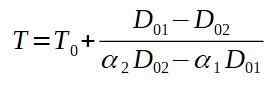
Następnie umieszczamy odpowiednie wartości.

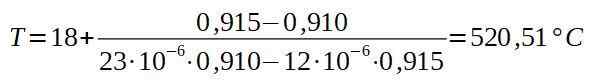
Wniosek jest taki, że piekarnik musi wynosić co najmniej 520,5 ° C, aby nit przeszedł przez otwór płyty aluminiowej.

Bibliografia

1. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. Szósta edycja. Prentice Hall. 238-249.
2. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. Mac Graw Hill. 422-527.