Różnice między prędkością i prędkością (z przykładami)

Różnice między prędkością a prędkością Istnieją, chociaż oba są powiązanymi ilościami fizycznymi. W wspólnym języku jeden lub drugi jest używany zamiennie, jakby były synonimiczne, ale w fizyce konieczne jest je odróżnić.

W tym artykule oba pojęcia są zdefiniowane, różnice są wskazane i wyjaśniane, przykładami, w jaki sposób i kiedy jedno lub drugi ma zastosowanie. Aby uprościć, rozważamy poruszającą się cząsteczką, a stamtąd przejmiemy pojęcia prędkości i prędkości. 

	Prędkość	Prędkość
Definicja	Jest to odległość przebywająca na jednostkę czasu.	To przemieszczenie (lub zmiana pozycji) w każdej jednostce czasu.
Notacja	v	v
Rodzaj obiektu matematycznego	Wspinać się.	Wektor.
Formuła (przez skończony okres)*	v = ΔS/ΔT	v = ΔR/ΔT
Formuła (przez chwilę danego czasu) **	v = ds/dt = s '(t)	v = dr/dt = r '(t)
Wyjaśnienie formuły	*Długość ścieżki przejechanej podzielona na okres używany do jej podróży.** W szybkości chwilowej rozpiętość czasu ma tendencję do zera. ** Operacja matematyczna jest pochodną łuku trajektorii w funkcji czasu w odniesieniu do czasu T.	*Przemieszczenie wektorowe podzielone przez okres, w którym wystąpiło przesunięcie. ** W szybkości chwilowej okres czasu ma tendencję do zera. ** Operacja matematyczna jest pochodną pozycji na czas.
Charakterystyka	Aby to wyrazić, wymagana jest tylko dodatnia liczba rzeczywista, niezależnie od wymiarów przestrzennych, w których występuje ruch. ** Natychmiastowa prędkość to bezwzględna wartość natychmiastowej prędkości.	W celu jej wyrażenia może być wymagana więcej niż jedna liczba rzeczywista (pozytywna lub ujemna), w zależności od wymiarów przestrzennych, w których ma miejsce. ** Moduł chwilowych prędkości jest natychmiastowy.

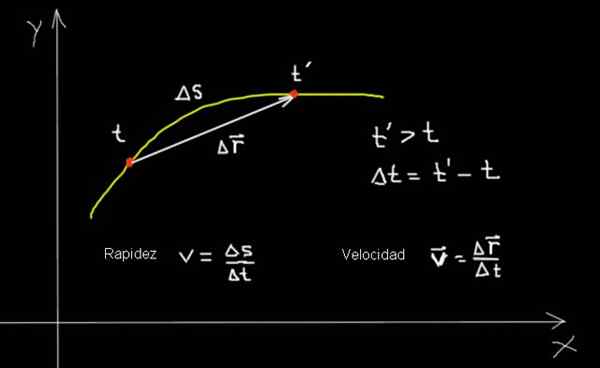
Przykłady z jednolitą szybkością na prostych sekcjach

Prędkość i prędkość cząstki, która porusza się w krzywej. Przygotowane przez: F. Zapata.

W poprzedniej tabeli podsumowano kilka aspektów prędkości i prędkości. A następnie uzupełnienie, uważa się, że kilka przykładów ilustruje związane z tym koncepcje i ich relacje:

Może ci służyć: paramagnetyzm

- Przykład 1

Załóżmy, że czerwona mrówek porusza się po linii prostej i w kierunku wskazanym na poniższym rysunku.

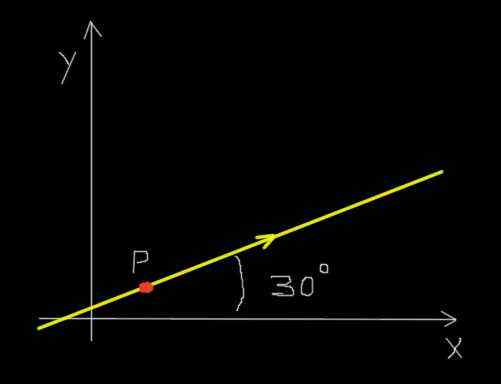Mrówka na ścieżce prostokątnej. Źródło: f. Zapata.

Ponadto mrówka porusza się równomiernie, tak że podróżuje w odległości 30 milimetrów w okresie 0,25 sekundy. 

Określić prędkość i prędkość mrówki.

Rozwiązanie 

Prędkość mrówki jest obliczana przez dzielenie odległości Δs Tourre Tour Δt.

V = δS/δT = (30 mm)/(0,25S) = 120 mm/s = 12 cm/s

Szybkość mrówek oblicza się poprzez podzielenie przemieszczenia ΔR między okresem, w którym dokonano wspomnianego wysiedlenia.

Przemieszczenie miało 30 mm w kierunku 30º w odniesieniu do osi x lub w zwartej formie: 

ΔR = (30 mm ¦ 30º)

Można zauważyć, że przemieszczenie składa się z wielkości i adresu, ponieważ jest to ilość wektorowa. Alternatywnie, przemieszczenie można wyrazić zgodnie z jego komponentami kartezjańskimi X i Y, w ten sposób:

ΔR = (30 mm* cos (30º); 30 mm* bez (30º)) = (25,98 mm; 15,00 mm)

Szybkość mrówki oblicza się poprzez podzielenie przemieszczenia między okresem, w którym został wykonany:

v = ΔR/Δt = (25,98 mm / 0,25 s; 15,00 mm / 0,25 s) = (103,92; 60,00) mm / s

Ta prędkość w komponentach kartezjańskich x i y w jednostkach CM/s to:

v = (10 392; 6000) cm/s.

Alternatywnie, wektor prędkości można wyrazić w postaci polarnej (kierunek modułu ¦), jak pokazano:

v = (12 cm/s ¦ 30º).

Notatka: W tym przykładzie, ponieważ prędkość jest stała, średnia prędkość i szybkość chwilowa pokrywają się. Udowodniono, że natychmiastowy moduł prędkości jest natychmiastowy.

Może ci służyć: gęstość

Przykład 2

Ta sama mrówka poprzedniego przykładu przechodzi od A do B, po B do C i wreszcie z C do A, podążając ścieżką trójkątną pokazaną na poniższej rysunku.

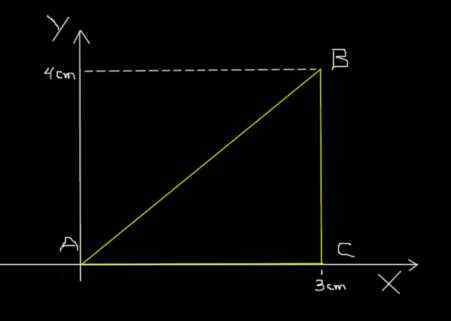Trójkątna ścieżka mrówki. Źródło: f. Zapata.

Sekcja AB podróżuje na 0,2S; BC przemieszcza się przy 0,1S i wreszcie CA podróżuje na 0,3S. Oblicz średnią prędkość trasy ABCA i średnią prędkość trasy ABCA.

Rozwiązanie 

Aby obliczyć średnią prędkość mrówki, zaczynamy od określenia całkowitego przebytego odległości:

ΔS = 5 cm + 4 cm + 3 cm = 12 cm.

Okres czasowy wykorzystywany na całą podróż jest:

ΔT = 0,2S + 0,1S + 0,3S = 0,6 s.

Tak więc średnia prędkość mrówki to:

V = δS/δT = (12 cm)/(0,6S) = 20 cm/s.

Następnie obliczana jest średnia prędkość mrówki na trasie ABCA. W takim przypadku przemieszczenie wykonane przez mrówek wynosi:

ΔR = (0 cm; 0 cm)

Wynika to z faktu, że przemieszczenie jest różnicą między pozycją końcową mniejszą pozycją początkową. Ponieważ obie pozycje są takie same, wówczas ich różnica jest nieważna, co powoduje przemieszczenie nieco.

To zerowe przemieszczenie przeprowadzono w okresie 0,6S, więc średni rodzaj mrówki wynosił:

v =(0 cm; 0 cm)/ 0,6S = (0; 0) cm/ s.

Wniosek: Średnia prędkość 20 cm/s, Ale średnia prędkość wynosi zero na trasie ABCA.

Przykłady z jednolitą szybkością na zakrzywionych sekcjach

Przykład 3

Owad porusza się po okręgu o promieniu 0,2 m z równomierną prędkością, tak że zaczynając od A i osiągając B, przemieszcza ¼ obwodu po 0,25 s.

Może ci służyć: prasa hydrauliczna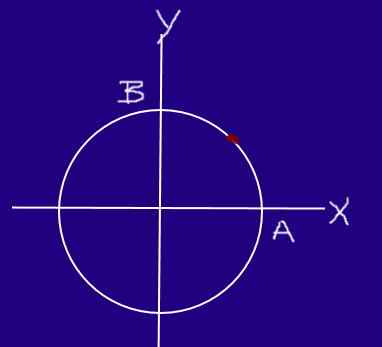Owady odcinka okrągłego. Źródło: f. Zapata.

Określ prędkość i prędkość owada w sekcji AB.

Rozwiązanie 

Długość obwodu między A i B wynosi:

ΔS = 2πr /4 = 2π (0,2 m) /4 = 0,32 m.

Stosując definicję średniej prędkości:

V = δS/δT = 0,32 m/0,25 s = 1,28 m/s.

Aby obliczyć średnią prędkość, konieczne jest obliczenie wektora przemieszczenia między pozycją początkową a a końcowym B:

ΔR = (0; r)-(r; 0) = (-r; r) = (-0,2; 0,2) m

Zastosowanie średniej definicji prędkości jest uzyskiwane:

v = ΔR/ ΔT = (-0,2; 0,2) m / 0,25S = (-0.8; 0,8) m/s.

Poprzednie wyrażenie to średnia prędkość między A i B wyrażona w postaci kartezjańskiej. Alternatywnie średnią prędkość można wyrazić w formie polarnej, to znaczy moduł i kierunek:

| v |. = ((-0,8)^2 + 0,8^2)^(½) = 1,13 m/s

Adres = arctan (0,8 / (-0,8)) = Arcan (-1) = -45º + 180º = 135º w odniesieniu do osi x.

Wreszcie, średni wektor prędkości w postaci polarnej to: v =(1,13 m/s ¦ 135º).

Przykład 4

Zakładając, że moment początkowy owada z poprzedniego przykładu wynosi 0s od punktu A, twoja pozycja wektorowa jest w jednej chwili, dowolne t, które są podane przez:

R(t) = [r cos ((π/2) t); R Sen ((π/2) t)].

Określ prędkość i natychmiastową prędkość w dowolnym momencie t.

Rozwiązanie 

Odwrotna prędkość jest pochodną w odniesieniu do czasu pozycji:

v(t) = DR/dt = [-r (π/2) bez ((π/2) t); R (π/2) cos ((π/2) t)]]]

Natychmiastowa prędkość to moduł natychmiastowej prędkości wektora:

v (t) = | v(T) |. = π r / 2^½

Bibliografia

1. Alonso m., Finn e. Fizyka Tom I: Mechanika. 1970. Międzyamerykańskie fundusz edukacyjny.DO.
2. Hewitt, str. Konceptualna nauka fizyczna. PIĄTA EDYCJA. osoba.
3. Młody, Hugh. Fizyka uniwersytecka z nowoczesną fizyką. 14. edycja. osoba.
4. Wikipedia. Prędkość. Odzyskane z: jest.Wikipedia.com
5. Zita, a. Różnica między prędkością a prędkością. Źródło:: wyróżnik.com