Ile rozwiązań ma równanie kwadratowe?

Równanie kwadratowe lub równanie drugiego stopnia może mieć zero, jedno lub dwa rzeczywiste roztwory, w zależności od współczynników, które pojawiają się we wspomnianym równaniu. Jeśli pracujesz nad liczbami złożonymi, możesz powiedzieć, że każde równanie kwadratowe ma dwa rozwiązania.

Aby rozpocząć równanie kwadratowe, jest to równanie formy AX²+Bx+C = 0, gdzie A, B i C są liczbami rzeczywistymi, a X jest zmienną.

Mówi się, że x1 jest rozwiązaniem poprzedniego równania kwadratowego, jeżeli podczas wymiany x przez x1 równanie jest spełnione, to znaczy, jeśli a (x1) ²+b (x1)+c = 0.

Jeśli masz na przykład równanie x²-4x+4 = 0, to X1 = 2 jest rozwiązaniem, ponieważ (2) ² (2) +4 = 4-8+4 = 0.

Przeciwnie, jeśli x2 = 0 zostanie zastąpione, uzyskuje się (0) ²-4 (0) +4 = 4, a jako 4 ≠ 0, to x2 = 0 nie jest rozwiązaniem równania kwadratowego.

Rozwiązania równania kwadratowego

Liczbę roztworów równania kwadratowego można oddzielić w dwóch przypadkach:

1.- W liczbach rzeczywistych

Podczas pracy z liczbami rzeczywistymi równania kwadratowe mogą mieć:

-Zero rozwiązań: Oznacza to, że nie ma rzeczywistej liczby, która spełnia równanie kwadratowe. Na przykład równanie podane x²+1 = 0, nie ma liczby rzeczywistych tak, że spełnia wspomniane równanie, ponieważ oba x² jest większe lub równe zero, a 1 jest większe niż zero, więc jego suma będzie większa, będzie większa, że ​​będzie większa Surowe niż zero.

-Powtarzające się rozwiązanie: Istnieje jedna realna wartość, która spełnia równanie kwadratowe. Na przykład jedynym rozwiązaniem równania x²-4x+4 = 0 jest x1 = 2.

-Dwa różne rozwiązania: Istnieją dwie wartości, które spełniają równanie kwadratowe. Na przykład x²+x -2 = 0 ma dwa różne roztwory, które są x1 = 1 i x2 = -2.

2.- W złożonych liczbach

Podczas pracy z liczbami złożonymi równania kwadratowe zawsze mają dwa rozwiązania, które są Z1 i Z2, gdzie Z2 jest koniugatem Z1. Ponadto można je zaklasyfikować jako:

-Kompleksy: Rozwiązania mają formę Z = p ± Qi, gdzie p i q są liczbami rzeczywistymi. Ta sprawa odpowiada pierwszemu przypadkowi poprzedniej listy.

-Czyste kompleksy: To wtedy, gdy prawdziwa część rozwiązania jest równa zero, to znaczy, że rozwiązanie ma formę Z = ± Qi, gdzie Q jest liczbą rzeczywistą. Ta sprawa odpowiada pierwszemu przypadkowi poprzedniej listy.

-Kompleksy z wyimaginowaną częścią równe zero: To wtedy, gdy złożona część rozwiązania jest równa zero, to znaczy, że rozwiązanie jest liczbą rzeczywistą. Ta sprawa odpowiada dwóch ostatnich przypadków poprzedniej listy.

Jak obliczane są roztwory równania kwadratowego?

Aby obliczyć roztwory równania kwadratowego, stosuje się formułę znaną jako „rozdzielczość”, która mówi, że roztwory równania osi+bx+c = 0 są podane przez wyrażenie następującego obrazu:

Ilość, która pojawia się w rdzeniu kwadratowym, nazywa się dyskryminacją równania kwadratowego i jest oznaczona literą „d”.

Równanie kwadratowe będzie miało:

-Dwa prawdziwe rozwiązania tak, i tylko tak, d> 0.

-Powtarzane prawdziwe rozwiązanie, jeśli i tylko jeśli, d = 0.

-Zero prawdziwe rozwiązania (lub dwa złożone rozwiązania) tak, i tylko tak, D<0.

Przykłady

-Rozwiązania równania x²+x-2 = 0 są podane przez:

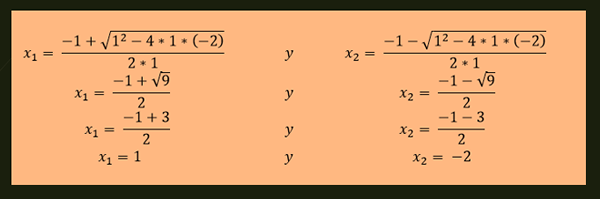
-Równanie x²-4x+4 = 0 ma powtarzane rozwiązanie, które jest podane przez:

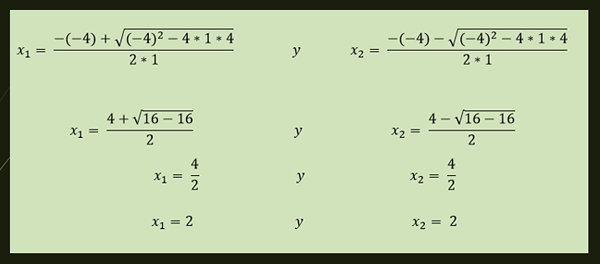
-Rozwiązania równania x²+1 = 0 są podane przez:

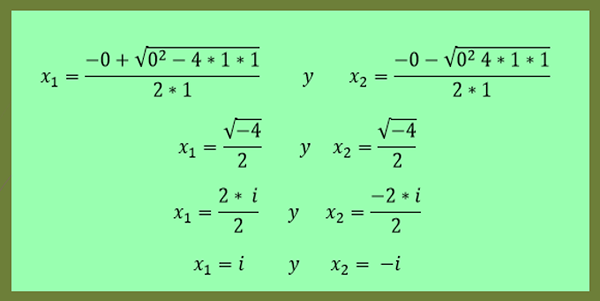
Jak widać w tym ostatnim przykładzie, x2 jest koniugatem x1.