Lina (geometria), twierdzenie i ćwiczenia

A lina, W płaskiej geometrii to segment linii łączy dwa punkty z krzywej. Mówi się, że linia zawierająca ten segment jest linią suszenia do krzywej. Często jest to obwód, ale z pewnością możesz wciągnąć sznurki do wielu innych krzywych, takich jak elipsy i przypowieści.

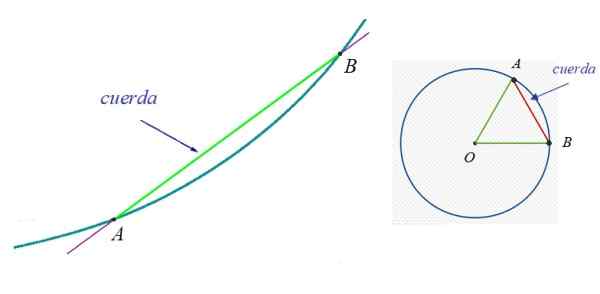
Na rycinie 1 po lewej stronie znajduje się krzywa, do której należą punkty a i b. Lina między A i B to zielony segment. Po prawej stronie jest obwód i jeden z ich strun, ponieważ możliwe jest śledzenie nieskończoności.

Rysunek 1. Po lewej stronie lina dowolnej krzywej i po prawej. Źródło: Wikimedia Commons.

W obwodzie jego średnica jest szczególnie interesująca, co jest również znane jako Główna lina. Jest to lina, która zawsze zawiera środek obwodu i mierzy dwa razy więcej promienia.

Poniższa rysunek jest reprezentowany przez promień, średnicę, linę, a także łuk koła. Prawidłowo zidentyfikuj każdy z nich jest ważny przy rozwiązywaniu problemów.

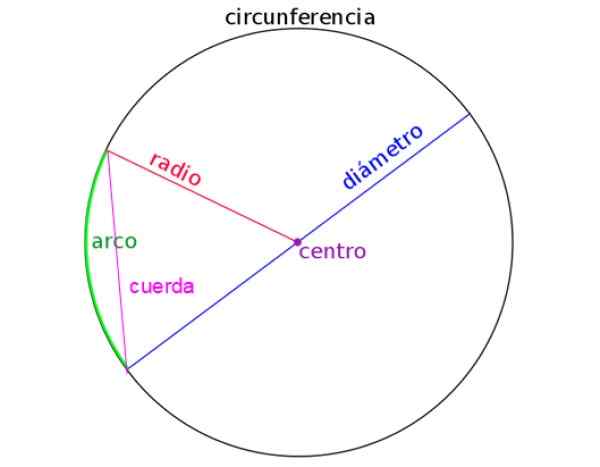Rysunek 2. Elementy obwodu. Źródło: Wikimedia Commons.

[TOC]

Długość liny obwodu

Możemy obliczyć długość liny w okręgu, zaczynając od rysunków 3a i 3b. Zauważ, że trójkąt jest zawsze tworzony z dwiema równymi stronami (izosceli): segmenty OA i OB, które mierzą r, promień obwodu. Trzecia strona trójkąta to segment ab, zwany C, który jest dokładnie długością liny.

Konieczne jest narysowanie linii prostopadłej do linii C do podziału pod kątem θ, który istnieje między dwoma radiotelefonami, a wierzchołek jest środkiem lub obwodem. To jest Kąt centralny -Ponieważ jego wierzchołek jest środkową, a linia bisektorowa jest również segntem do obwodu.

Może ci służyć: radykalne właściwości

Natychmiast powstają dwa prostokąty, których przeciwprostokąt. Ponieważ dwusa'a, a wraz z nią średnica, dzieli się na dwie części równe linie, okazuje się, że jedna z nóg ma połowę C, jak wskazano na ryc. 3B.

Z definicji piersi kąta:

sin (θ/2) = przeciwny/hipotenusa cateto = (c/2)/r

Dlatego:

sin (θ/2) = c/2r

C = 2r Sen (θ/2)

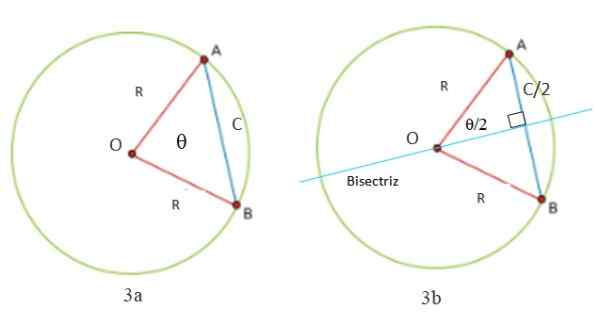Rysunek 3. Trójkąt utworzony przez dwa radiotelefony i lina obwodu to izosceles (ryc. 3), ponieważ ma on dwie strony. Bisektor dzieli go na dwa trójkąty prostokątne (ryc. 3B). Źródło: Przygotowane przez F. Zapata.

Twierdzenie o strumieniu 

Twierdzenie o łańcuchu mówi:

Jeśli w jednym punkcie przecinają się jakakolwiek dwie liny, iloczyn długości segmentów, które pojawiają się na jednym ze strun, jest równy iloczynowi długości segmentów, które są zdefiniowane w drugiej linie.

Poniższy rysunek pokazuje dwa struny tego samego obwodu: AB i CD, które przecinają się w punkcie P. W linie AB segmenty AP i Pb są zdefiniowane, podczas gdy CP i PD są zdefiniowane w linii CD. Następnie, zgodnie z twierdzeniem:

AP . PB = CP . P.S

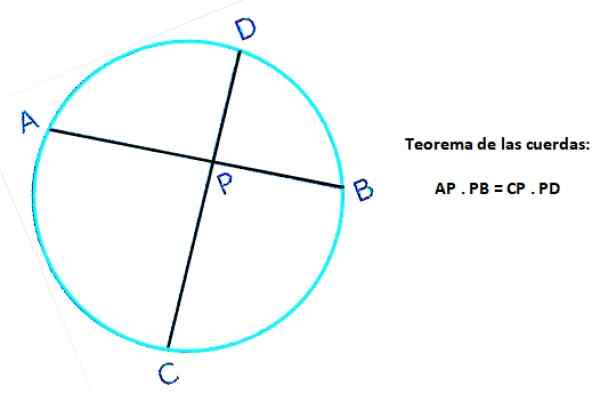Rysunek 4. Twierdzenie liny obwodu. Źródło: f. Zapata.

Rozwiązane Ćwiczenia

- Ćwiczenie 1

Okrąg ma linę 48 cm, która znajduje się 7 cm od środka. Oblicz powierzchnię koła i obwód obwodu.

Rozwiązanie  

Aby obliczyć okrąg obszar, wystarczy znać promień obwodu na kwadrat, ponieważ jest on wypełniony:

A = π.R²

Teraz liczba utworzona z dostarczanymi danymi jest trójkąt prostokąta, którego nogi wynoszą odpowiednio 7 i 24 cm.

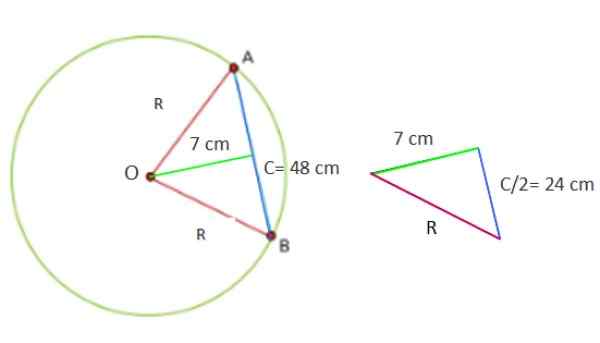Rysunek 5. Geometria rozwiązanego ćwiczenia 1. Źródło: f. Zapata.

Dlatego znalezienie wartości r² Twierdzenie Pitagoras C jest stosowane bezpośrednio² = a² + B², Ponieważ r jest hipotenuem trójkąta:

Może ci służyć: kąt zerowy: definicja i cechy, przykłady, ćwiczenia

R² = (7 cm)² + (24 cm)² = 625 cm²

Następnie żądany obszar to:

A = π. 625 cm² = 1963.5 cm²

Jeśli chodzi o obwód lub długość L obwodu, jest on obliczany przez:

L = 2π. R

Wymiana wartości:

R = √625 cm² = 25 cm

L = 2π. 25 cm = 157.1 cm.

- Ćwiczenie 2

Określić długość liny okręgu, którego równanie to:

X² + I² - 6x - 14Y -111 = 0

Wiadomo, że współrzędne środkowego punktu liny to P (17/2; 7/2).

Rozwiązanie

Punkt środkowy linii nie należy do obwodu, ale ekstremalne punkty liny tak. Problem można rozwiązać za pomocą wcześniej określonego twierdzenia o strunach, ale najpierw jest to wygodne.

Krok 1: Uzyskaj kanoniczne równanie obwodu

Kanoniczne równanie obwodu z środkiem (H, K) to:

(X-H)² + (Y-K)² = R²

Aby go uzyskać, konieczne jest wypełnienie kwadratów:

(X² - 6x) + (i² - 14Y) -111 = 0

Zauważ, że 6x = 2.(3x) i 14Y = 2.(7y), aby poprzednie wyrażenie zostało przepisane w ten sposób, pozostanie niezmienionym:

(X² - 6x+3²-3²) + (i² - 14Y+7²-7²) -111 = 0

A teraz, pamiętając o definicji znaczącego produktu (A-B)² = a² - 2AB + b² Można go napisać:

(X - 3)² - 3² + (i - 7)² - 7² - 111 = 0

= (x - 3)² + (i - 7)² = 111 + 3² + 7² → (x - 3)² + (i - 7)² = 169

Obwód ma środek (3.7) i radio r = √169 = 13. Poniższy rysunek pokazuje wykres obwodu i ciągów, które będą używane w twierdzeniu:

Może ci służyć: jakie są 7 elementów obwodu?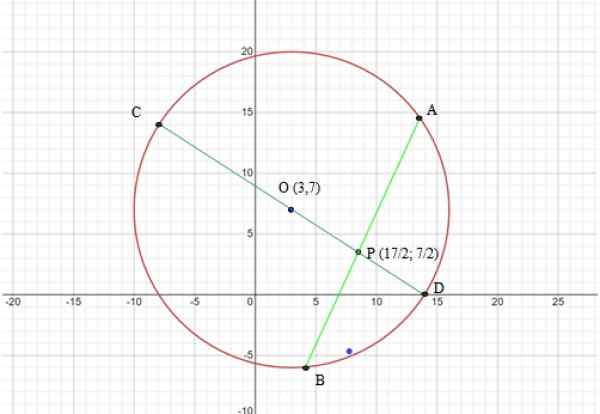Rysunek 6. Wykres obwodu ćwiczenia rozwiązanego 2. Źródło: f. Zapata za pośrednictwem internetowego kalkulatora matematyki.

Krok 2: Określ segmenty do użycia w twierdzeniu

Segmenty do użycia są ciągami CD i AB, zgodnie z ryc. 6, oba są wycięte w punkcie P, dlatego:

CP . PD = AP. Pb

Teraz znajdziemy odległość między punktami O i P, ponieważ da nam to długość segmentu OP. Jeśli dodamy promień do tej długości, będziemy mieli segment CP.

Odległość d_Op Między dwoma punktami współrzędnymi (x₁,I₁) i (x₂,I₂) Jest:

D_Op² = Op² = (x₂ - X₁)² + (I₂ - I₁)² = (3- 17/2)² + (7-7/2)² = 121/4 + 49/4 = 170/4

D_Op = Op = √170 /2

Przy wszystkich uzyskanych wynikach, a także wykres, budujemy następującą listę segmentów (patrz rysunek 6):

Co = 13 cm = r

OP = √170 /2 cm

CP = OP + R = 13 + √170 /2 cm

PD = OD - OP = 13 - √170 /2 cm

AP = Pb

2.AP = długość liny

Zastąpienie w twierdzeniu String:

CP . PD = AP . Pb = [(13 +√170 /2) . (13 --√170 /2)] = AP²

[169-170/4] = AP²

253/2 = AP²

AP = √ (253/2)

Długość liny wynosi 2.AP = 2 (√253/2) = √506

Czy czytelnik mógłby rozwiązać problem w inny sposób?

Bibliografia

1. Baldor, a. 2004. Płaska i przestrzeń geometria z trygonometrią. Publikacje kulturalne s.DO. c.V. Meksyk.
2. C-K12. Spożycie akordu. Odzyskane z: CK12.org.
3. Escobar, J. Obwód. Odzyskane z: matematyki.Ty.Edu.współ.
4. Villena, m. Stożkowy. Źródło: DSPACE.Espol.Edu.Ec.
5. Wikipedia. Lina (geometria). Odzyskane z: jest.Wikipedia.org.