Opis twierdzenia Nortona, aplikacje, przykłady i ćwiczenia

On Twierdzenie Nortona, który dotyczy obwodów elektrycznych, ustala, że ​​obwód liniowy z dwoma zaciskami A i B może zostać zastąpiony innym całkowicie równoważnym, składającym się z obecnego źródła o nazwie I_NIE połączone równolegle z oporem r_NIE.

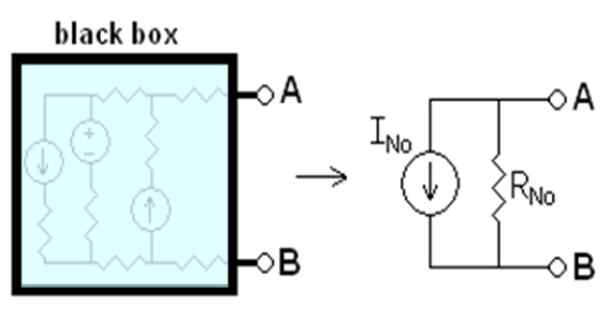
Powiedział obecny ja_NIE słyszałem_N Jest to ten, który płynąłby między punktami A i B, gdyby były krótkie -obwód. Opór r_N Jest to równoważna oporność między terminalami, gdy wszystkie niezależne źródła są dezaktywowane. Wszystko, co powiedziane, jest schematyzowane na rycinie 1.

Rysunek 1. Równoważny obwód Nortona. Źródło: Wikimedia Commons. Drumkid [CC BY-SA 3.0 (http: // creativeCommons.Org/licencje/by-sa/3.0/]]

Czarna skrzynka na rysunku zawiera obwód liniowy, który zostanie zastąpiony jego odpowiednikiem Norton. Obwód liniowy to taki, w którym wejście i wyjście mają zależność liniową, na przykład związek między napięciem V a prądem stałym I w elemencie omowym: v = i.R.

To wyrażenie odpowiada prawu Ohma, gdzie R jest oporem, co może być również impedancją, jeśli jest to obwód prądowy naprzemiennie.

Twierdzenie Nortona zostało opracowane przez elektrycznego i wynalazcę Edwarda L. inżyniera. Norton (1898–1983), który przez długi czas pracował dla Bell Laboratories.

[TOC]

Zastosowania Norton Twierdzenie

Kiedy mają bardzo skomplikowane sieci, z wieloma oporem lub impedancjami i chcesz mniejszego i łatwiejszego obwodu.

W ten sposób twierdzenie Nortona jest bardzo ważne przy projektowaniu obwodów z wieloma elementami, a także do zbadania ich odpowiedzi.

Związek między twierdzeniami Norton i Thevenina

Twierdzeniem Nortona jest twierdzenie podwójnego thenina, co oznacza, że ​​są równoważne. Twierdzenie Thevenina wskazuje, że czarne skrzynkę na rycinie 1 można zastąpić źródłem napięcia szeregowego z rezystancją, zwaną opornością_Th. Jest to wyrażone na poniższym rysunku:

Może ci służyć: mechanika materialna: historia, dziedzina studiów, zastosowania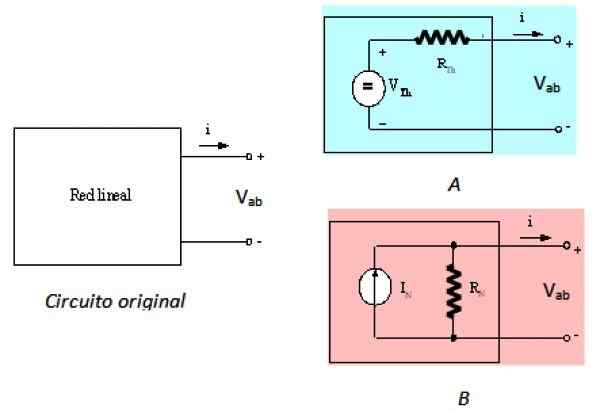 Rysunek 2. Oryginalny lewicowy obwód i jego odpowiedniki z Thévenin i Norton. Źródło: f. Zapata.

Lewy obwód to oryginalny obwód, sieć liniowa w czarnej polu, obwód w prawo jest odpowiednikiem Thevenin i obwodu B Jest to odpowiednik Nortona, jak opisano. Widoczne z terminali A i B, trzy obwody są równoważne.

Teraz obserwuj to:

-W oryginalnym obwodzie napięcie między zaciskami wynosi v_Ab.

-V_Ab  = V_Th w obwodzie DO

-Wreszcie v_Ab  = I_N.R_N w obwodzie B

Jeśli zaciski A i B są zwarciami w trzech obwodach, należy spełnić, że napięcie i prąd między tymi punktami muszą być takie same dla tych trzech, ponieważ są równoważne. Więc:

-W oryginalnym obwodzie prąd to ja.

-W przypadku obwodu A prąd to i = v_Th / R_Th, Zgodnie z prawem Ohma.

-Wreszcie w obwodzie B prąd to ja_N

Dlatego stwierdzono, że rezystancje Nortona i Thevenin mają tę samą wartość i że prąd jest podany przez:

i = i_N = V_Th / R_Th = V_Th / R_N

Przykład

Aby poprawnie zastosować twierdzenie Nortona, wykonane są następujące kroki:

-Sekcja obwodu, dla której równoważnik Nortona zostanie znaleziony z sieci, jest izolowany z sieci.

-W pozostałym obwodzie wskazuj terminale A i B.

-Wymień źródła napięcia na krótkie obwody i prądowe na otwarte obwody, aby znaleźć równoważną rezystancję między zaciskami A i B. To jest r_N.

-Zwróć wszystkie źródła do ich pierwotnych pozycji, krótko -obwód terminali A i B i znajdź prąd, który krąży między nimi. To jestem ja_N.

Może Ci służyć: Doppler Efekt: Opis, wzory, przypadki, przykłady

-Narysuj obwód równoważny Nortona zgodnie z tym, co jest wskazane na rycinie 1. Zarówno źródło prądu, jak i równoważna rezystancja są równoległe.

Możesz także zastosować twierdzenie Thevenina, aby znaleźć r_Th, To, co już wiemy, jest równe R_N, Następnie przez prawo Ohma możesz znaleźć ja_N I powstały obwód jest narysowany.

A teraz spójrzmy na przykład:

Znajdź odpowiednik Nortona między punktami A i B następującego obwodu:

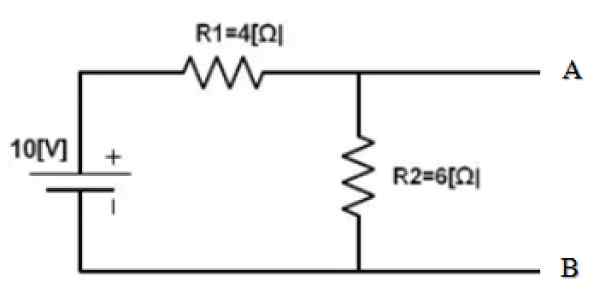Rysunek 3. Przykładowy obwód. Źródło: f. Zapata.

Część obwodu jest już izolowana, której równoważny należy znaleźć. A punkty A i B są wyraźnie określone. Poniżej znajduje się zwarcie źródła 10 V i znalezienie równoważnej rezystancji uzyskanego obwodu:

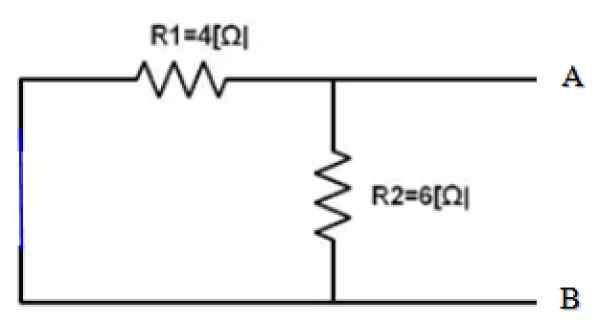Rysunek 4. Krótkie Źródło obwodu. Źródło: f. Zapata.

Widoki z terminali A i B, obie oporności r₁ i r₂ Dlatego są równoległe:

1/r_Eq = 1/r₁₂ = (1/4) + (1/6) ω^-1 = 5/12 Ω^-1  → R_Eq = 12/5 Ω = 2.4 Ω

Następnie źródło jest zwracane na swoje miejsce, a punkty A i B są krótkie -obwód, aby znaleźć prąd, który tam krąży, to będzie_N. W tym wypadku:

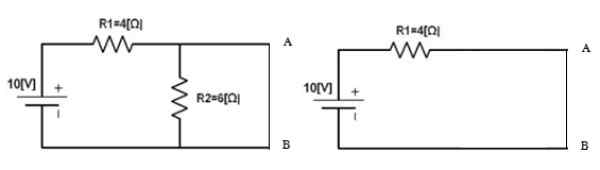Rysunek 5. Obwód do obliczenia prądu Norton. Źródło: f. Zapata.

Siema_N = 10 v / 4 Ω = 2.5 a

Norton równoważny

Wreszcie narysowany jest odpowiednik Nortona z znalezionymi wartościami:

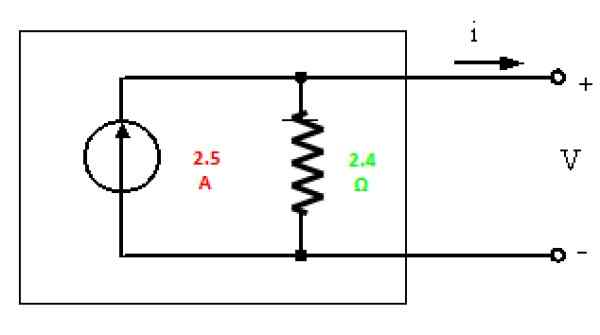Rysunek 6. Norton równoważny obwodu na rycinie 3. Źródło: f. Zapata.

Ćwiczenie rozwiązane

W obwodzie poniższego rysunku:

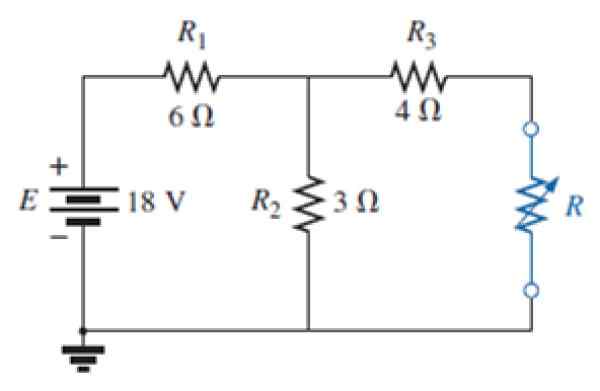Rysunek 7. Obwód do ćwiczenia rozwiązany. Źródło: Alexander, C. 2006. Podstawy obwodów elektrycznych. 3. Wydanie. MC Graw Hill.

a) Znajdź równoważny obwód Nortona zewnętrznej sieci rezystancji niebieskiej.

b) Znajdź także odpowiednik Thévenina.

Rozwiązanie

Zgodnie z powyższymi krokami źródłem musi być krótkie -obwodu:

Może ci służyć: dyfrakcja dźwięku: co składa się z przykładów, aplikacji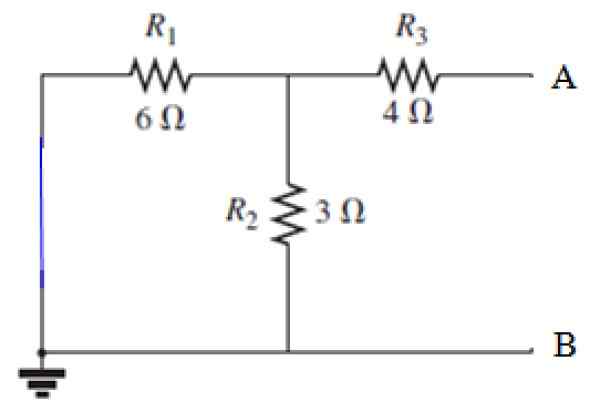 Cyfra 8. Krótkie źródło obwodu w obwodzie na ryc. 7. Źródło: f. Zapata.

Obliczanie RN

Widok z terminali A i B, opór r₃ jest szeregowo z równoległością utworzoną przez rezystancje r₁ i r₂, Najpierw obliczmy równoważny opór tej równoległości:

1/r₁₂ = (1/6)+ (1/3) ω^-1 = 1/2 Ω^-1  → R_Eq = 2/1 Ω = 2Ω

A potem ta paralela jest szeregowo z r_3, tak że równoważny opór jest:

R_Eq = 2 Ω + 4 Ω = 6 Ω

To jest wartość obu r_N od r_Th, Jak wyjaśniono wcześniej.

Obliczanie w

Następnie terminale A i B są krótkie, zwracając źródło na swoje miejsce:

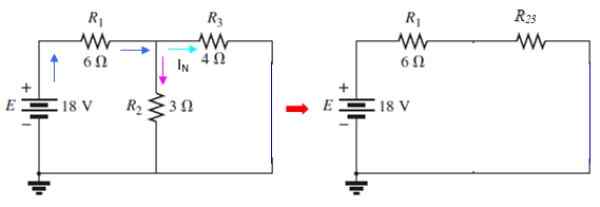Rysunek 9. Obwody prądowe Norton. Źródło: f. Zapata.

Obecny przechodzi przez ja₃ jest obecny i_N poszukiwane, które można określić metodą siatki lub za pomocą serii i równoległych. W tym obwodzie r₂ i r₃ Są równoległe:

1/r₂₃ = (1/3)+ (1/4) ω^-1 = 7/12 Ω^-1  → R₂₃ = 12/7 Ω

Opór r₁ Jest w szeregu z tą równoległą, zatem:

R₁₂₃ = 6 + (12/7) Ω = 54/7 Ω

Prąd, który wychodzi ze źródła (niebieski kolor), jest obliczany przez prawo Ohma:

V = i. R → i = v/r = 18 v/(54/7 Ω) = 7/3 a

Ten prąd jest podzielony na dwie części: jedna, która przecina r₂ I kolejny, który przecina r₃. Jednak prąd, który przekracza równoległe r₂₃ To samo, co przechodzi przez r₁, Jak widać w obwodzie pośrednie. Napięcie jest:

V₂₃ = I.R₂₃ = (7/3) a .(12/7) ω = 4 V

Obie oporności r₂ i r₃ Są na tym napięciu, ponieważ są równoległe, dlatego:

Siema₃ = V₂₃ / R₃ = 4 v / 4 Ω = 1 a

Mamy już prąd Norton, ponieważ jak wcześniej powiedziałem₃ = I_N, Więc:

Siema_N = 1 a

Norton równoważny

Wszystko jest gotowe narysować odpowiednik tego obwodu między punktami A i B:

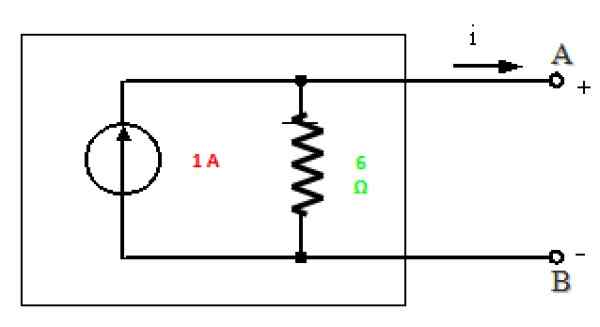Rysunek 10. Norton równoważny obwodu na ryc. 7. Źródło: f. Zapata.

Rozwiązanie b

Znalezienie odpowiednika Thévenina jest bardzo proste, ponieważ r_Th = R_N= 6 Ω i jak wyjaśniono w poprzednich sekcjach:

V_Th = I_N. R_N = 1 a . 6 Ω = 6 V

Równoważny obwód Thévenina to:

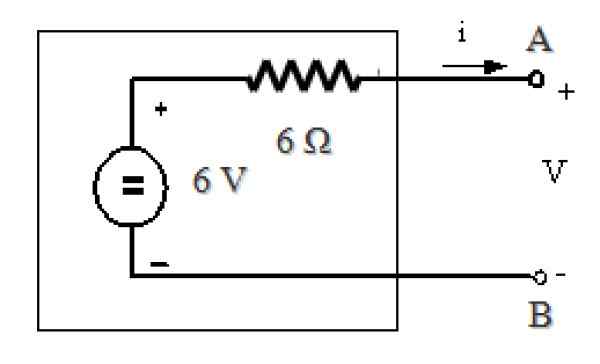Rysunek 11. Równoważny obwodu na ryc. 7. Źródło: f. Zapata.

Bibliografia

1. Alexander, c. 2006. Podstawy obwodów elektrycznych. 3. Wydanie. MC Graw Hill.
2. Boylestad, r. 2011. Wprowadzenie do analizy obwodów. 2. Wydanie. osoba.
3. Dorf, r. 2006. Wprowadzenie do cyrków elektrycznych. 7th. Wydanie. John Wiley & Sons.
4. Edminister, j. 1996. Obwody elektryczne. Seria Schaum. 3. Wydanie. MC Graw Hill.
5. Wikipedia. Twierdzenie Nortona . Odzyskane: to jest.Wikipedia.org.