Definicja i charakterystyka kątu zerowego, przykłady, ćwiczenia

On kąt zerowy Jest to ten, którego miara jest warta 0, zarówno w stopniach, jak i w promietach lub innym systemie pomiarowym. Dlatego brakuje mu amplitudy lub otwierania, na przykład jedną między dwiema równolegle.

Chociaż jego definicja brzmi dość prosto, kąt zerowy jest bardzo przydatny w wielu aplikacjach fizyki i inżynierii, a także w nawigacji i projektowaniu.

Rysunek 1. Pomiędzy prędkością a przyspieszeniem samochodu jest kąt zerowy, dlatego samochód idzie szybciej i szybciej. Źródło: Wikimedia Commons.

Istnieją wielkości fizyczne, które należy wyrównać równolegle, aby osiągnąć pewne efekty: jeśli samochód porusza się prosto na autostradzie i między jego wektorem prędkości v i jego przyspieszenie wektora Do Jest 0º, samochód rośnie.

Na poniższym rysunku pojawiają się różne typy kąta, w tym kąt zerowy po prawej stronie. Jak widać, kąt 0 brakuje amplitudy lub otwarcia.

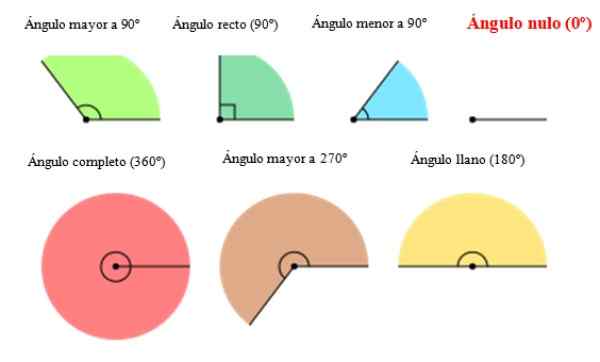Rysunek 2. Rodzaje kąta, w tym kąt zerowy. Źródło: Wikimedia Commons. Orias [CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0)].[TOC]

Przykłady kątów zerowych

Wiadomo, że linie równoległe tworzą kąt zerowy. Kiedy masz linię poziomą, jest to równoległe do osi x kartezjańskiego układu współrzędnych, dlatego jego skłonność do niego wynosi 0. Innymi słowy, linie poziome mają zerowe zbocze.

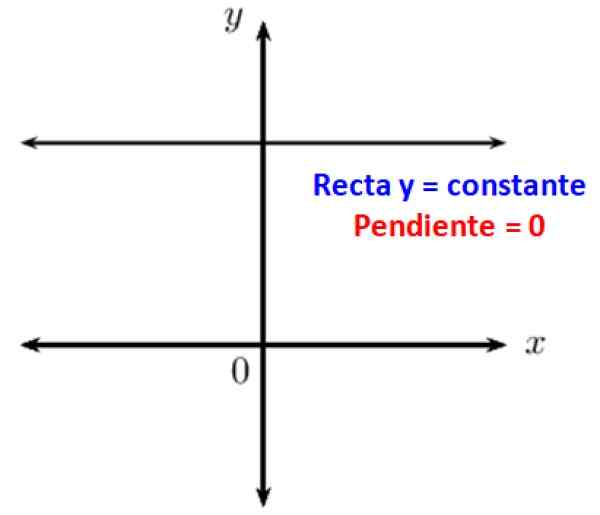Rysunek 3. Linie poziome mają zerową oczekującą. Źródło: f. Zapata.

Również trygonometryczne przyczyny kąta zerowego wynoszą 0, 1 lub nieskończoność. Dlatego kąt zerowy jest obecny w wielu sytuacjach fizycznych, które obejmują operacje z wektorami. Te powody to:

Może ci służyć: Para uporządkowana

-Sen 0º = 0

-cos 0º = 1

-TG 0º = 0

-Sec 0º = 1

-Szkoda 0º → ∞

-CTG 0º → ∞

I będą przydatne do analizy niektórych przykładów sytuacji, w których obecność kąt zerowego odgrywa fundamentalną rolę:

- Wpływ kąt zerowych na wielkości fizyczne

Suma wektorów

Gdy dwa wektory są równoległe, kąt między nimi jest zerowy, jak pokazano na rycinie 4 powyżej. W tym przypadku suma obu jest przeprowadzana przez umieszczenie jednego po drugiej, a wielkość sumy wektora jest sumą wielkości dodatków (ryc. 4B).

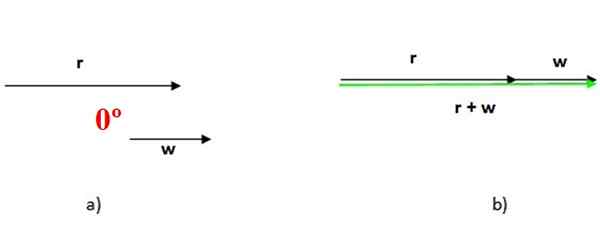Rysunek 4. Suma równoległych wektorów, w tym przypadku kąt między nimi jest kątem zerowym. Źródło: f. Zapata.

Gdy dwa wektory są równoległe, kąt między nimi jest zerowy, jak pokazano na rycinie 4 powyżej. W tym przypadku suma obu jest przeprowadzana przez umieszczenie jednego po drugiej, a wielkość sumy wektora jest sumą wielkości dodatków (ryc. 4B)

Moment obrotowy lub moment obrotowy

Moment obrotowy lub moment obrotowy powoduje obrót ciała. Zależy to od wielkości przyłożonej siły i tego, jak się stosuje. Bardzo reprezentatywnym przykładem jest angielski klucz postaci.

Aby osiągnąć najlepszy efekt zakrętu, siła prostopadle dotyczy klawisza, w górę lub w dół, ale obrót nie jest oczekiwany, jeśli siła jest równoległa do uchwytu.

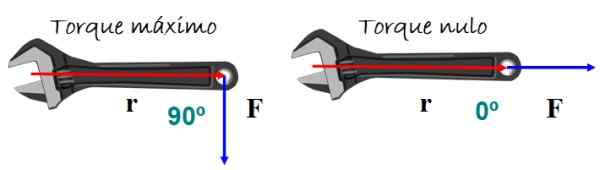Rysunek 5. Gdy kąt między wektorami położenia a wytrzymałością jest nieważny, moment obrotowy nie występuje i dlatego nie ma efektu zwrotnego. Źródło: f. Zapata.

Matematycznie moment obrotowy τ Jest zdefiniowany jako wektor lub produkt krzyżowy między wektorami R (wektor pozycji) i F (Wektor siły) z rysunku 5:

Może ci służyć: gałęzie statystyczne

τ = r X F

Wielkość momentu obrotowego wynosi:

τ = r f sen θ

Będąc θ kątem między R I F. Gdy sin θ = 0 moment obrotowy jest nieważny, w takim przypadku θ = 0º (lub także 180º).

Przepływ pola elektrycznego

Przepływ pola elektrycznego jest wielkością skalarną, która zależy od intensywności pola elektrycznego, a także od orientacji powierzchniowej, przez którą się przecina.

Na rycinie 6 istnieje okrągła powierzchnia powierzchni A, przez którą przechodzą linie pola elektrycznego I. Orientacja powierzchniowa jest podawana przez normalny wektor N. Po lewej stronie pole i normalny wektor tworzą arbitralny kąt θ, w środku tworzą kąt zerowy, a prawa są prostopadłe.

Gdy I I N Są prostopadłe, linie pola nie przecinają powierzchni, a zatem przepływ wynosi zero, podczas gdy kąt pomiędzy I I N Jest puste, linie całkowicie przecinają powierzchnię.

Oznaczając przepływ pola elektrycznego przez grecką literę φ (odczytuje „FI”), jego definicję dla pola jednolitego, jak na rysunku, pozostaje tak:

Φ = I• •NDO

Punkt pośrodku obu wektorów oznacza produkt punktowy lub skalarny, co na przemian określa:

Φ = I• •NA = eacosθ

Bold i strzałki nad literą są zasobami do rozróżnienia wektora od jego wielkości, co jest oznaczone normalnymi literami. Ponieważ cos 0 = 1 przepływ jest maksymalny, gdy I I N Są równoległe.

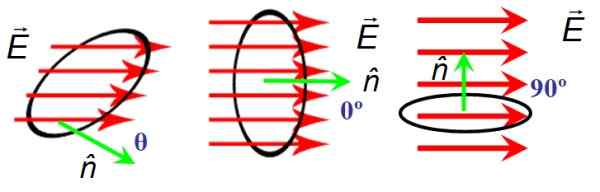Rysunek 6. Przepływ pola elektrycznego zależy od orientacji między powierzchnią a polem elektrycznym. Źródło: f. Zapata.

Ćwiczenia

- Ćwiczenie 1

Dwie siły P I Q Działają jednocześnie na terminowym obiekcie x, obie siły początkowo tworzą kąt θ. Co stanie się z wielkością powstałej siły, gdy θ maleje, aż zostanie odwołana?

Może ci służyć: ocena funkcji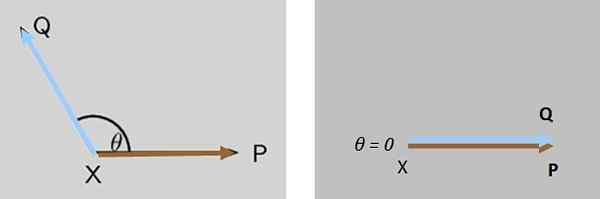 Rysunek 7. Kąt między dwiema siłami działającymi na ciało maleje, aż wielkość powstałej siły nabywa jej maksymalną wartość w tym przypadku. Źródło: f. Zapata.

Rozwiązanie

Wielkość powstałej siły Q + P Stopniowo rośnie, aż będzie maksymalnie, gdy Q I P Są całkowicie równoległe (ryc. 7 po prawej).

- Ćwiczenie 2

Wskaż, czy kąt zerowy jest rozwiązaniem następującego równania trygonometrycznego:

cos 2x = 1 + 4se x

Rozwiązanie

Równanie trygonometryczne to takie, w którym nieznane jest częścią argumentu rozumu trygonometrycznego. Aby rozwiązać proponowane równanie, wygodne jest skorzystanie z wzoru dla cosinusa podwójnego kąta:

cos 2x = cos² X - Sen² X

Ponieważ w ten sposób argument po lewej stronie staje się X zamiast 2x. Więc:

sałata² X - Sen² x = 1 + 4sen x

Z drugiej strony, cos² X + Sen² x = 1, więc:

sałata² X - Sen² x = cos² X + Sen² x + 4Sen x

Termin cos² X jest anulowany i pozostaje:

- Sen² x = sen² x + 4Sen x → - 2Sen² X - 4Senx = 0 → 2Sen² x + 4Senx = 0

Teraz dokonana jest kolejna zmiana zmiennej: Senx = U i równanie jest przekształcone w:

2U² + 4u = 0

2U (U+4) = 0

Którego rozwiązania to: u = 0 i u = -4. Zwracając zmianę, mielibyśmy dwie możliwości: sin x = 0 i senx = -4. To ostatnie rozwiązanie nie jest opłacalne, ponieważ pierś dowolnego kąta wynosi od -1 do 1, więc pozostaje nam pierwsza alternatywa:

sin x = 0

Dlatego x = 0º jest rozwiązaniem, ale również obsługuje dowolny kąt, którego sinus jest 0, który może również wynosić 180º (π radian), 360º (2 π radian), a także odpowiednie negatywy również.

Najbardziej ogólnym rozwiązaniem równania trygonometrycznego jest: x = kπ gdzie k = 0, ± 1, ± 2, ± 3, .. . K Numer liczb całkowitych.

Bibliografia

1. Baldor, a. 2004. Płaska i przestrzeń geometria z trygonometrią. Publikacje kulturalne s.DO. c.V. Meksyk.
2. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 3. Układy cząstek. Pod redakcją Douglas Figueroa (USB).
3. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 5. Interakcja elektryczna. Pod redakcją Douglas Figueroa (USB).
4. Onlinematlearning. Rodzaje kątów. Pobrano z: onlinematlearning.com.
5. Zill, d. 2012. Algebra, trygonometria i geometria analityczna. McGraw Hill Inter -American.