Koncepcja kompresji i wzory, obliczenia, przykłady, ćwiczenia

wysiłek kompresji lub kompresji Jest to siła na jednostkę obszaru, którego rezultatem jest pchanie, dokręcenie lub kompresja obiektu, dążenie do go skrócenie. Matematycznie to:

E = f /a

Tutaj I Oznacz wysiłek, F wielkość siły i DO Obszar, na którym jednostka znajduje się w systemie międzynarodowym, jeśli Newton/m² o Pascal (PA). Wysiłek kompresji to normalny wysiłek, ponieważ siła, która go wytwarza, jest prostopadła do obszaru, na którym jest wywierana.

Rysunek 1. Kolumny w akropolii Atenach podlegają kompresji. Źródło: Pixabay.

Taki wysiłek może skompresować obiekt lub wręcz przeciwnie, dokręcić i rozciągnąć, zgodnie z zastosowaniem. W przypadku wysiłku kompresyjnego siły mają zastosowanie w przeciwnym kierunku, aby wywierać efekt dokręcenia i skracania obiektu.

Gdy siły ustąpi, wiele materiałów powraca do ich pierwotnych wymiarów. Ta właściwość jest znana pod nazwą elastyczność. Ale choć tak się dzieje, jednolite deformacja elastyczna cierpiąca z powodu materiału podlegającego wysiłku jest:

Odkształcenie jednolitowe = (rozmiar końcowy - wielkość początkowa)/początkowa rozmiar

Deformacja może być liniowa, powierzchowna lub objętość, chociaż odkształcenie jednostkowe brakuje jednostek. Jednak informacje, które podaje, są bardzo ważne, ponieważ nie jest takie samo, aby odkształcić pręt o długości 10 m o długości 1 cm, aby odkształcić 1 cm Kolejne 1 m długości.

W elastycznym materiale deformacja i wysiłek są proporcjonalne, zgodne z prawem Hooke:

Wysiłek ∝ Jednostkowe deformacje

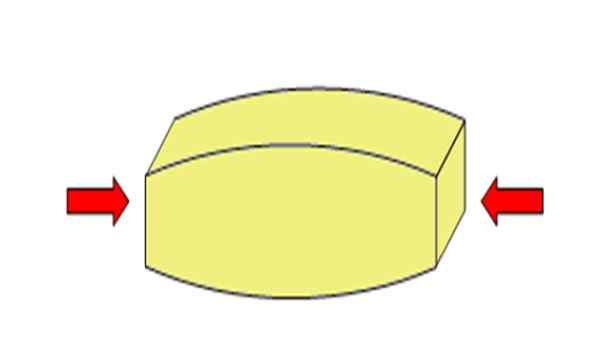Rysunek 2. Wysiłek kompresji zmniejsza długość obiektu. Źródło: Wikimedia Commons. Adre-es [CC BY-SA 4.0 (https: // creativeCommons.Org/licencje/nabrzeże/4.0)].[TOC]

¿Jak obliczyć kompresję?

Wysiłek kompresji sprawia, że ​​cząstki materiału zbliżają się. W zależności od kierunku stosowania wysiłku, nastąpi skrócenie lub zmniejszenie dowolnego z jego wymiarów.

Może ci służyć: kwantowy model mechaniczny atomu

Zacznijmy od przyjęcia cienkiego paska o pierwotnej długości L,  do którego stosuje się normalny wysiłek wielkości I. Jeśli wysiłek jest kompresja, pasek doświadcza zmniejszenia swojej długości, oznaczonej przez δ. Jeśli jest to napięcie, pasek zostanie przedłużony.

Oczywiście materiał, którego element jest podejmowany, jest decydujący pod względem zdolności do wspierania wysiłków.

Te elastyczne cechy materiału są zawarte we wyżej wymienionych stałej proporcjonalności. Jest nazywany Moduł elastyczności albo Młody moduł i jest to oznaczone jako i. Każdy materiał ma moduł elastyczności, który jest określany eksperymentalnie za pomocą testów laboratoryjnych.

Mając to na uwadze, wysiłek I Jest wyrażany w sposób matematyczny taki:

Wysiłek ∝ Jednostkowe deformacje

Wreszcie, aby ustalić ten warunek jako równanie, wymagana jest stała proporcjonalności, aby zastąpić symbol proporcjonalności ∝ i zastąpienie go równością, tak:

Wysiłek = stała proporcjonalność x deformacja jednostki        

E = y. (Δ /l)

Iloraz (Δ /l) Jest to jednolite deformacja, oznaczona jako ε i z δ = Końcowa długość - długość początkowa. W ten sposób wysiłek I Pozostaje jak:

E = y. ε

Ponieważ odkształcenie jednostki jest bezwymiarowe, jednostki I są takie same jak te I: N/m² lub PA w systemie SI, funty/in² o psi w systemie brytyjskim, a także inne kombinacje siły i obszaru, takie jak kg/cm².

Moduł elastyczności różnych materiałów

Wartości i są określane eksperymentalnie w laboratorium, w kontrolowanych warunkach. Następnie moduł elastyczności materiałów szeroko stosowanych w budownictwie, a także kości:

Może ci służyć: wektory w przestrzeni: jak wykres, aplikacje, ćwiczenia

Tabela 1

Materiał	Moduł elastyczności Y (PA) x 109
Stal	200
Żelazo	100
Mosiądz	100
Brązowy	90
Aluminium	70
Marmur	pięćdziesiąt
Granit	Cztery pięć
Beton	20
Kość	piętnaście
Drewno sosnowe	10

Przykłady

Wysiłki kompresyjne działają na różnych strukturach; To samo, które podlegają działaniu sił, takich jak waga każdego z elementów, które je komponują, a także siły z czynników zewnętrznych: wiatr, śnieg, inne struktury i wiele innych.

Zwykle jest to, że większość struktur jest zaprojektowana tak, aby oprzeć się wszelkiego rodzaju wysiłkom bez deformacji. Dlatego konieczne jest uwzględnienie wysiłków kompresji, aby uniemożliwić utracie jego kształtu lub obiekt.

Również kości szkieletu są strukturami podlegającymi różnym wysiłkom. Chociaż kości są na nie odporne, gdy limit sprężysty jest przekraczany przez przypadek, szczeliny i złamania pochodzą.

Kolumny i filary

Kolumny i filary budynków muszą być wyprodukowane, aby oprzeć się kompresji, w przeciwnym razie mają tendencję do ustalenia. To jest znane jako zgięcie boczne albo wyboczenie.

Kolumny (patrz ryc. 1) to elementy, których długość jest znacznie wyższa w porównaniu z obszarem jej przekroju.

Element cylindryczny to kolumna, gdy jego długość jest równa lub większa niż dziesięć razy większa niż średnica przekroju. Ale jeśli przekrój nie jest stały, jego mniejsza średnica zostanie pobrana w celu sklasyfikowania elementu jako kolumny.

Krzesła i banki

Kiedy ludzie zajmują miejsce w meblach, takich jak krzesła i banki, lub dodają obiekty na górze, nogi podlegają wysiłkom kompresji, które mają tendencję do zmniejszania wysokości.

Rysunek 3. Siedząc, ludzie wywierają wysiłek kompresyjny na krześle, który ma tendencję do skracania ich wzrostu. Źródło: Pixabay.

Zwykle meble są wytwarzane, aby całkiem dobrze oprzeć ciężarowi i powrócić do ich naturalnego stanu po jego usunięciu. Ale jeśli wielka waga jest przywiązana do kruchych krzeseł lub brzegów, nogi dają kompresję i pękanie.

Może ci służyć: przewody elektryczne

Ćwiczenia

- Ćwiczenie 1

Masz pręt, który pierwotnie mierzy długość 12 m, do którego ulega wysiłku kompresji, tak że jego deformacja jednostkowa wynosi -0.0004. Jaka jest nowa długość pręta?

Rozwiązanie

Zaczynając od równania podanego powyżej:

ε = (Δ /l) = - 0.0004

Tak L_F Jest to końcowa długość i L_albo początkowa długość, ponieważ δ = L_F - L_albo  Ty masz:

(L_F - L_albo)/ L_albo = -0.0004

Dlatego: L_F - L_albo = -0.0004 x 12 m = -0.0048 m. I w końcu:

L_F  = (12–0.0048) M = 11.9952 m.

- Ćwiczenie 2

Stały stalowy pręt, cylindryczny, mierzy 6 m długości i średnicy 8 cm. Jeśli pręt jest poddawany kompresji za pomocą obciążenia 90.000 kg, znajdź:

a) Wielkość wysiłku kompresji w megapascalu (MPA)

b) Ile spadła długość paska?

Rozwiązanie

Pierwszy jest obszar A przekroju paska, który zależy od jego średnicy D, co skutkuje:

A = π. D² / 4 = π. (0.08 m)² / 4 = 5.03 x 10^-3 M²

Siła jest natychmiast, przez F = m.G = 90.000 kg x 9.8 m/s²= 882.000 n.

Wreszcie średni wysiłek jest obliczany w następujący sposób:

E = f/ a = 882.000 N/ 5.03 x 10^-3 M² = 1.75 x 10⁸ PA = 175 MPa

Rozwiązanie b

Równanie wysiłku jest teraz używane, wiedząc, że materiał ma elastyczną odpowiedź:

E = y. (Δ /l)

Moduł stalowy jest znaleziony w tabeli 1:

δ = e.L / y = 6 m x 1.75 x 10⁸ PA / 200 x 10 ⁹ PA = 5.25 x 10 ^-3 M = 5.25 mm.

Bibliografia

1. Piwo, f. 2010. Mechanika materiałów. 5. Wydanie. McGraw Hill.
2. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^Tth  Wyd. Prentice Hall.
3. Hibbeler, R.C. 2006. Mechanika materiałów. 6th. Wydanie. Edukacja Pearsona.
4. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. McGraw Hill
5. Wikipedia. Stres (mechanika). Odzyskane z: Wikipedia.org.