Prostokątne elementy wektora (z ćwiczeniami)

prostokątne składniki wektora to dane, które składają się na ten wektor. Aby je ustalić, konieczne jest posiadanie układu współrzędnych, który zwykle jest płaszczyzną kartezjańską.

Po uzyskaniu wektora w układzie współrzędnych można obliczyć jego komponenty. Są to 2, składnik poziomy (równolegle do osi x), zwany „komponentem w osi x”, i komponent pionowy (równolegle do osi y), zwany „komponentem w osi y” ”.

Graficzna reprezentacja prostokątnych składników wektora

Aby określić komponenty, jest to konieczne.

[TOC]

Jak określić prostokątne składniki wektora?

Aby określić te elementy, należy znać pewne zależności między prostokątami i funkcjami trygonometrycznymi.

Na poniższym obrazie możesz zobaczyć ten związek.

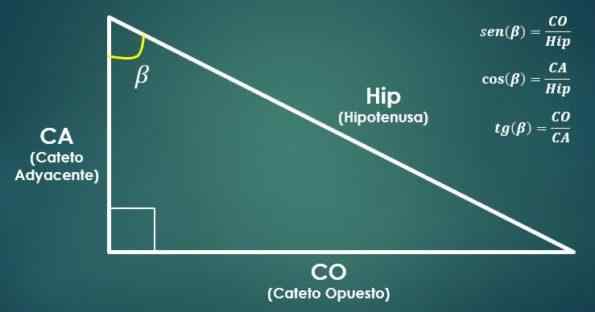Związki między prostokątami a funkcjami trygonometrycznymi

Bosom kąta jest równy ilorazowi między miarą kateto przeciwnej do kąta a miarą hipotenu.

Z drugiej strony, cosinus kąta jest równy iloraz między miarą Cateto przylegającej do kąta a miarą hipotenu.

Styczna kąta jest równa ilorazie między miarą przeciwnej nogi a miarą sąsiedniego cateto.

We wszystkich tych relacjach konieczne jest ustanowienie odpowiedniego trójkąta prostokąta.

Czy są inne metody?

Tak. W zależności od dostarczonych danych sposób obliczenia prostokątnych składników wektora może się różnić. Kolejnym narzędziem, które jest często używane, jest twierdzenie Pitagoras.

Może ci służyć: twierdzenie o istnieniu i wyjątkowości: demonstracja, przykłady i ćwiczenia

Rozwiązane ćwiczenia

Następujące ćwiczenia wprowadzone w życie definicja prostokątnych składników wektora i relacje opisane powyżej.

Pierwsze ćwiczenie

Wiadomo, że wektor A ma wielkość równą 12, a kąt, że ta forma z osą x ma miarę 30 °. Określ prostokątne elementy wspomnianego wektora.

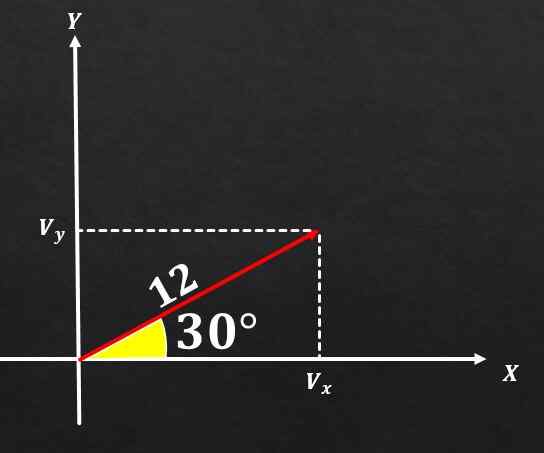
Rozwiązanie

Jeśli obraz jest doceniany, a formuły opisane powyżej są używane, można stwierdzić, że komponent w i wektorze A jest równy

sin (30 °) = vy / 12, a zatem vy = 12*(1/2) = 6.

Z drugiej strony komponent na osi x wektora A jest równy

cos (30 °) = VX / 12, a zatem VX = 12*(√3 / 2) = 6√3.

Drugie ćwiczenie

Jeśli wektor A ma wielkość równą 5, a komponent na osi x jest równy 4, określ wartość komponentu A na osi y.

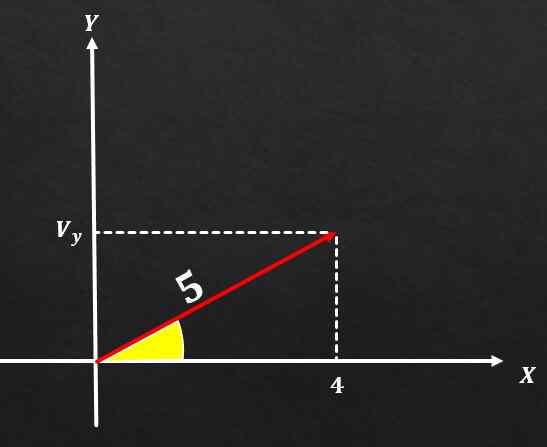
Rozwiązanie

Za pomocą twierdzenia Pitagorasa wielkość wektora wysoka kwadrat musi być równa sumie kwadratów dwóch prostokątnych składników. To znaczy m² = (vx) ² + (vy) ².

Zastępując dostarczone wartości, musisz

5² = (4) ² + (vy) ², a zatem 25 = 16 + (vy) ².

Oznacza to, że (vy) ² = 9, a zatem vy = 3.

Trzecie ćwiczenie

Jeśli wektor A ma wielkość równą 4, co tworzy kąt 45 ° z osą x, określ prostokątne składniki wspomnianego wektora.

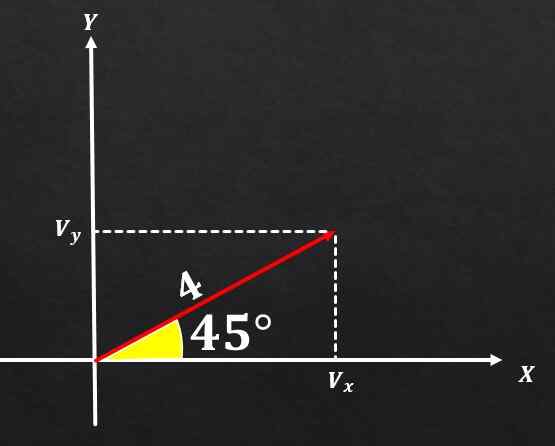
Rozwiązanie

Korzystając z zależności między trójkątem prostokąta a funkcjami trygonometrycznymi, można stwierdzić, że komponent na i wektorze A jest równy

sin (45 °) = vy / 4, a zatem vy = 4*(√2 / 2) = 2√2.

Z drugiej strony komponent na osi x wektora A jest równy

Może ci służyć: sukcesja złożona

cos (45 °) = vx / 4, a zatem vx = 4*(√2 / 2) = 2√2.

Bibliografia

1. Landaverde, f. D. (1997). Geometria (Przedruk ed.). Postęp.
2. Leake, d. (2006). Trójkąty (Ilustrowany ed.). Heinemann-Raintree.
3. Pérez, c. D. (2006). Przedłużanie. Edukacja Pearsona.
4. Ruiz, á., I Barrantes, H. (2006). Geometrie. CR technologia.
5. Sullivan, m. (1997). Przedłużanie. Edukacja Pearsona.
6. Sullivan, m. (1997). Trygonometria i geometria analityczna. Edukacja Pearsona.