Zewnętrzne alternatywne ćwiczenia i ćwiczenia rozstrzygnięte

Zewnętrzne alternatywne kąty Są to kąty, które powstają, gdy dwie równoległe linie są przechwycone za pomocą linii suszenia. Oprócz tych kątów powstaje inny moment obrotowy, które nazywane są wewnętrznymi alternatywnymi kątami.

Różnica między tymi dwoma pojęciami to słowa „zewnętrzne” i „wewnętrzne” i jak wskazano nazwa, zewnętrzne alternatywne kąty to te, które są tworzone poza dwiema równolegle.

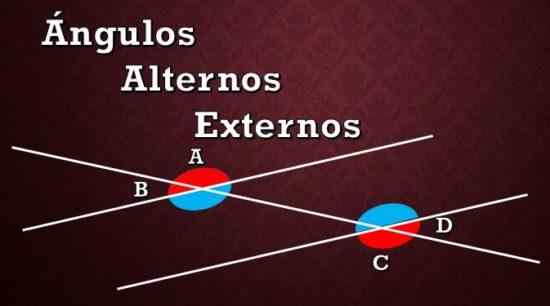
Graficzna reprezentacja alternatywnych kątów zewnętrznych A, B i C, D

Jak widać na poprzednim obrazie, między dwiema równolegle i linią suszenia powstaje osiem kąty. Czerwone kąty są zewnętrzną alternatywą, a niebieskie kąty są wewnętrznymi alternatywnymi kątami.

[TOC]

Charakterystyka zewnętrznych alternatywnych kątów

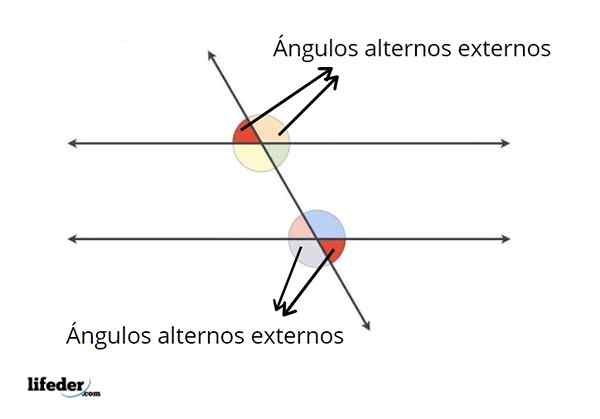Przykłady zewnętrznych alternatywnych kątów

We wstępie zostało już wyjaśnione, jakie są zewnętrzne alternatywne kąty. Oprócz bycia zewnętrznymi kątami między podobieństwami, kąty te spełniają inny warunek.

Warunkiem, które spełniają, jest to, że zewnętrzne alternatywne kąty utworzone na linii równoległej są zgodne; Ma taką samą miarę jak pozostałe dwa, które powstają na drugiej linii równoległej.

Ale każdy zewnętrzny alternatywny kąt jest zgodny z tym po drugiej stronie linii sekund.

Jakie są przystające zewnętrzne alternatywne kąty?

Jeśli zaobserwowano obraz początku i poprzednie wyjaśnienie, można stwierdzić, że zewnętrzne alternatywne kąty, które są ze sobą zgodne: kąty A i C oraz kąty B i D.

Aby wykazać, że są one zgodne.

Może ci służyć: stała funkcja: cechy, przykłady, ćwiczenia

Rozwiązane ćwiczenia

Poniżej znajduje się seria ćwiczeń, w których definicja i własność zgodności zewnętrznych kątów należy zastosować.

Pierwsze ćwiczenie

Na poniższym obrazie, jaka jest miara kąta A wiedząc, że kąt E mierzy 47 °?

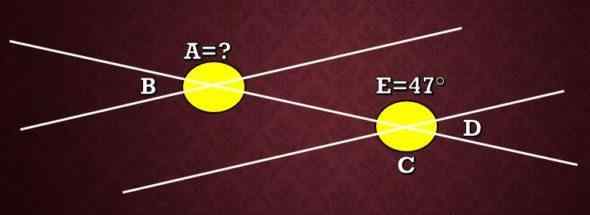
Rozwiązanie

Jak wyjaśniono wcześniej, Angles A i C są zgodne z tym, że są zewnętrzne. Dlatego miara a jest równa miarę C. Teraz, ponieważ kąty E i C są przeciwnymi kątami przez wierzchołek, mają one taką samą miarę, dlatego miara C wynosi 47 °.

Podsumowując, miara wynosi 47 °.

Drugie ćwiczenie

Oblicz miarę kąta C pokazaną na poniższym obrazie, wiedząc, że kąt B mierzy 30 °.

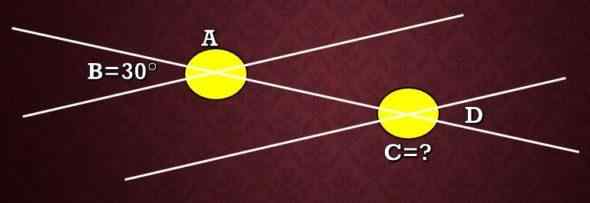
Rozwiązanie

W tym przykładzie używana jest definicja. Dwa kąty są uzupełniające, jeśli suma ich miar jest równa 180 °.

Na obrazie można zauważyć, że A i B są uzupełniające, a zatem A+B = 180 °, to znaczy w+30 ° = 180 °, a zatem a = 150 °. Teraz, podobnie jak A i C są zewnętrznymi alternatywnymi kątami, więc jego miary są takie same. Dlatego miara C wynosi 150 °.

Trzecie ćwiczenie

Na poniższym obrazie miara kąta A wynosi 145 °. Jaka jest miara kąta E?

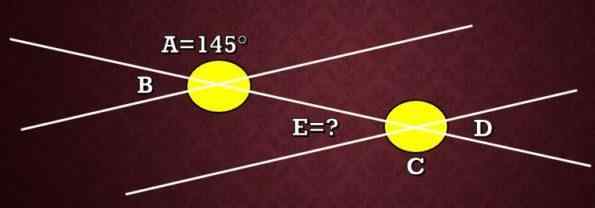
Rozwiązanie

Na obrazie można zobaczyć, że kąty A i C są zewnętrznymi alternatywnymi kątami, dlatego mają one tę samą miarę. To znaczy, że miara C wynosi 145 °.

Ponieważ kąty C i E są kątami uzupełniającymi, muszą to wynosić C+E = 180 °, czyli 145 °+E = 180 °, a zatem miara kąta E wynosi 35 °.

Może ci służyć: Błąd próbkowania: wzory i równania, obliczenia, przykłady

Bibliografia

1. Bourke. (2007). Kąt w skoroszycie matematyki geometrii. Nauka Newpath.
2. C. I. DO. (2003). Elementy geometrii: z licznymi ćwiczeniami i geometrią kompasu. University of Medellin.
3. Clemens, s. R., O'Dafer, s. 1. G., & Cooney, t. J. (1998). Geometria. Edukacja Pearsona.
4. Lang, s., & Murrow, G. (1988). Geometria: kurs szkoły średniej. Springer Science & Business Media.
5. Lira, a., Jaime, s. 1., Chavez, m., Gallegos, m., I Rodríguez, C. (2006). Geometria i trygonometria. Umbral Editions.
6. Moyano, a. R., Saro, a. R., & Ruiz, r. M. (2007). Algebra i geometria kwadratowa. Netbiblo.
7. Palmer, c. Siema., & Bibb, s. F. (1979). Praktyczna matematyka: arytmetyka, algebra, geometria, trygonometria i reguła obliczeń. Rectte.
8. Sullivan, m. (1997). Trygonometria i geometria analityczna. Edukacja Pearsona.
9. Wingard-Enelson, r. (2012). Geometria. Enslow Publishers, Inc.