Koncepcja współczynnika koncepcji, wzór, obliczenia, przykład

On Współczynnik restytucji Jest to iloraz między względną prędkością prędkości a względną prędkością zbliżania się dwóch ciał. Kiedy ciała są zjednoczone po zderzeniu, ten iloraz jest nieważny. A jednostka jest warta w przypadku, gdy zderzenie jest idealnie elastyczne.

Załóżmy, że dwie stałe sfer masy M1 i masa M2 odpowiednio, że cierpią na zderzenie. Tuż przed kolizją kule miały prędkości V1 I V2 Odnośnie określonego systemu odniesienia bezwładnościowego. Zaraz po zderzeniu ich prędkości zmieniają się na V1 ' I V2 '.

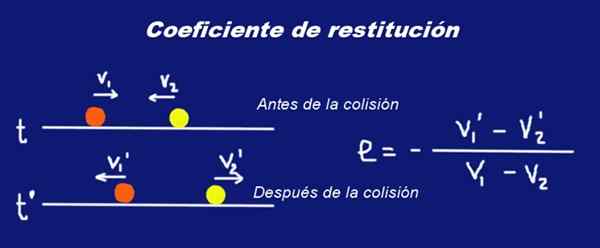Rysunek 1. Zderzenie dwóch sfer mas M1 i M2 oraz ich współczynnik restytucji i. Przygotowane przez Ricardo Pérez.

List został umieszczony pogrubiona czcionka W prędkościach wskazujących, że są to wielkości wektorowe.

Eksperymenty wskazują, że każda kolizja spełnia następujący związek:

V1 ' - V2 '= -I (V1 - V2)

Gdzie I Jest to liczba rzeczywista od 0 do 1, nazywana Współczynnik restytucji kolizji. Poprzednie wyrażenie jest interpretowane w następujący sposób: 

Względna prędkość dwóch cząstek przed zderzeniem jest proporcjonalna do względnej prędkości dwóch cząstek po zderzeniu, stała proporcjonalności wynosi (-e), gdzie e jest współczynnikiem zwrotu kolizji.

[TOC]

Jaki jest współczynnik restytucji?

Przydatność tego współczynnika polega na poznaniu stopień nieelastyczności zderzenia. W przypadku, gdy zderzenie jest całkowicie elastyczne, współczynnik wynosił 1, podczas gdy w całkowicie nieelastycznej zderzeniu współczynnik będzie wart 0, ponieważ w tym przypadku względna prędkość po zderzeniu jest null.

Wzajemnie, jeśli współczynnik restytucji zderzenia i prędkości cząstek są znane przed nią, prędkości można przewidzieć po wystąpieniu takiej kolizji. 

Może ci służyć: 13 przykładów pierwszego prawa Newtona w prawdziwym życiu

Pęd

W kolizjach, oprócz relacji ustanowionych przez współczynnik restytucji, istnieje inny fundamentalny związek, którym jest Ochrona pędu.

Pęd P cząstki lub ilości ruchu, jak się nazywa, jest to iloczyn masy M cząstki dla jej prędkości V. To znaczy: pęd P Jest to kwota wektorowa.

W zderzeniach liniowy pęd P System jest taki sam tuż przed i tuż po zderzeniu, ponieważ siła zewnętrzna jest nikczemna na krótkie, ale intensywne siły interakcji wewnętrznej podczas zderzenia. Ale ochrona pędu nie wystarczy P systemu do rozwiązania ogólnego problemu zderzenia.

W wspomnianym wcześniej przypadku, z których kolidują dwie kulki M1 i M2, zachowanie pędu liniowego jest napisane w ten sposób:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Nie ma możliwości rozwiązania problemu zderzenia, jeśli współczynnik zwrotu nie jest znany. Ochrona pędu, choć konieczna, jest niewystarczająca do przewidywania prędkości po zderzeniu.

Kiedy problem stwierdza, że ​​ciała poruszają się razem po zderzeniu, domyślnie mówi, że współczynnik zwrotu wynosi 0.

Rysunek 2. W piłkach bilardowych istnieją zderzenia współczynnika zwrotu niewiele niż 1. Źródło: Pixabay.

Współczynnik energii i zwrotu 

Inną ważną ilością fizyczną zaangażowaną w kolizje jest energia. Podczas kolizji istnieją wymiana energii kinetycznej, energii potencjalnej i innych rodzajów energii, takich jak energia kaloryczna.

Przed kolizją i po zderzeniu energia potencjalna interakcji jest praktycznie zerowa, więc bilans energetyczny obejmuje energię kinetyczną cząstek przed i po i po czym Q nazywany rozproszoną energią.

Może ci służyć: model atomowy Heisenberga

Dla dwóch sfer mas M1 i M2, które zderzają bilans energetyczny przed i po zderzeniu, jest napisane tak:

½ m1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + Q

Kiedy siły interakcji podczas kolizji są czysto konserwatywne, tak się zdarza Całkowita energia kinetyczna Z zderzających się cząstek, które są zachowane, to znaczy jest to samo przed i po zderzeniu (q = 0). Kiedy tak się dzieje, mówi się, że kolizja jest idealnie elastyczna.

W przypadkach kolizji sprężystej energia nie jest rozpraszana. A także współczynnik zwrotu jest zgodny: E = 1. 

Przeciwnie, w zderzeniach nieelastycznych, które ≠ 0 i 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Aby problem z zderzeniem był doskonale ustalony, konieczne jest znanie współczynnika zwrotu lub naprzemiennie ilość energii rozproszonej podczas kolizji.

Współczynnik restytucji zależy od charakteru i rodzaju interakcji między dwoma ciałami podczas zderzenia.

Z drugiej strony względna prędkość ciał przed zderzeniem zdefiniuje intensywność interakcji, a tym samym jej wpływ na współczynnik restytucji. 

Jak obliczono współczynnik zwrotu?

Aby zilustrować, w jaki sposób obliczany jest współczynnik restytucji zderzenia, weźmiemy prosty przypadek:

Załóżmy, że zderzenie dwóch sfer masowych M1 = 1 kg I M2 = 2 kg ten porusza się na prostym tarciu (jak na rycinie 1).

Pierwsza kula wpływa na początkową prędkość V1 = 1 m/s Około sekundy, która jest pierwotnie w spoczynku, to znaczy V2 = 0 m/s.

Może ci służyć: pierwsze prawo termodynamiki: wzory, równania, przykłady

Po zderzeniu poruszają się w ten sposób: pierwszy zatrzymuje się (V1 '= 0 m/s) i drugi porusza się w prawo z prędkością V2 '= 1/2 m/s.

Aby obliczyć współczynnik restytucji w tej kolizji, stosujemy związek:

V1 ' - V2 ' = -I ( V1 - V2 ) 

0 m/s - 1/2 m/s = - e (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Przykład

W jednym wymiarowym zderzeniu dwóch sfer poprzedniej sekcji obliczono jego współczynnik zwrotu, co skutkuje E = ½ .

Ponieważ e ≠ 1 zderzenie nie jest sprężyste, to znaczy energia kinetyczna systemu nie jest zachowana i istnieje pewna ilość rozproszonej energii q (na przykład podgrzewanie kulek z powodu zderzenia).

Określić wartość energii rozproszonej w dżuli. Oblicz także procentową część rozproszonej energii.

Rozwiązanie

Początkowa energia kinetyczna kuli 1 to: 

K1i = ½ m1 v1^2 = ½ 1 kg (1 m/s)^2 = ½ j

Podczas gdy Sphere 2 jest zero za początkowo w spoczynku.

Więc początkowa energia kinetyczna systemu to ki = ½ j.

Po zderzeniu tylko druga kula porusza się z prędkością V2 '= ½ m/s, więc ostateczna energia kinetyczna systemu będzie:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ j

Oznacza to, że energia rozproszona w zderzeniu jest:

Q = Ki - kf = (½ J - ¼ J) = 1/4 J

A ułamek energii rozproszonej w tej zderzeniu oblicza się w następujący sposób:

F = q / ki = ¼ / ½ = 0,5, to znaczy, że 50% energii systemowej zostało rozproszone z powodu zderzenia nieelastycznego, którego współczynnik zwrotu wynosi 0,5.

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill.
2. Figueroa, zm. 2005. Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
3. Knight, r. 2017. Fizyka dla naukowców i inżynierii: podejście strategiczne. osoba.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
5. Wikipedia. Ilość ruchu.Odzyskane z: jest.Wikipedia.org.