Współczynnik współczynnika Poissona, wzory, wartości, przykłady

On Współczynnik Poissona Jest to bezwymiarowa ilość, charakterystyczna dla każdego materiału. Wskazuje na deformację kawałka materiału przed zastosowaniem niektórych wysiłków.

Kiedy materiał materialny, który ulega napięciu lub kompresji, cierpi deformacja, iloraz między odkształceniem poprzecznym a deformacją wzdłużną jest dokładnie współczynnik Poissona.

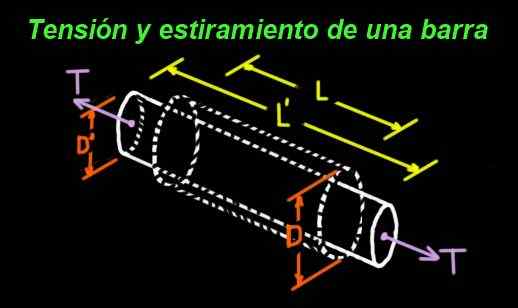
Rysunek 1. Współczynnik Poissona mierzy związek między rozciąganiem podłużnym a skęaniem poprzecznym. (Przygotowane przez Ricardo Pérez)

Na przykład gumowy cylinder, który ulega napięciu na jego końcach, jest rozciągnięty w kierunku podłużnym, ale jest poprzecznie wąski. Rysunek 1 pokazuje pasek, którego oryginalne wymiary to: długa L i średnica D.

Pasek podlega napięciem t, a w wyniku tego napięcia cierpi na rozciąganie, tak że nowa długość wynosi l '> l. Ale podczas rozciągania zwężenie jej średnicy następuje również nowa wartość: D ' < D.

Iloraz między rozciąganiem (dodatnie) a zwężeniem (ujemnym) pomnożonym przez (-1), jest liczbą dodatnią między 0 a 0,5. Ta liczba jest współczynnikiem Poissona ν SAM (list grecki).

[TOC]

Formuła współczynnika Poissona

Aby obliczyć współczynnik Poissona, konieczne jest określenie deformacji podłużnej i poprzecznej jednostki.

Deformacja jednostki podłużnej ε_L Jest to odcinek podzielony między pierwotną długość:

ε_L = (L ' - l) / l

Podobnie, poprzeczne jednolite odkształcenie ε_T Jest to zwężenie promieniowe podzielone między pierwotną średnicę:

ε_T = (D ' - d) / d

Dlatego współczynnik Poissona jest obliczany w następującym wzorze:

ν = - ε_T / ε_L 

Związek z modułem elastyczności i modułem sztywności

Współczynnik Poissona ν jest związany z modułem I elastyczności (lub młody moduł) i z modułem sztywności G, według następującej formuły:

Może ci służyć: optyka geometryczna: jakie badania, prawa, zastosowania, ćwiczenia

ν = e /(2G) - 1

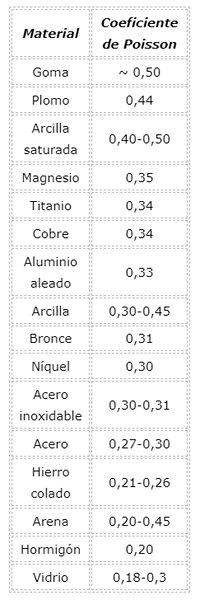
Wartość współczynnika Poissona dla materiałów

Rysunek 2. Stal nierdzewna ma współczynnik Poissona między 0,30 a 0,31. Źródło: Pixabay.

Przykłady obliczeń

Przykład 1

Pasek określonego materiału z tworzywa sztucznego ma długość 150 mm i odcinka okrągłego o średnicy 20 mm. Gdy siła ściskająca 612,25 kg-F jest poddawana sile ściskającej, obserwuje się skrócenie 14 mm i jednocześnie wzrost o 0,85 mm w średnicy słupka.

Oblicz:

a) Podłużne jednolite odkształcenie.

b) Transversalne jednolite deformacja.

c) współczynnik tego materiału Poissona.

d) moduł elastyczności Younga odpowiadający materiałowi.

e) Moduł sztywności tego plastiku.

Rozwiązanie

Przypomnijmy, że deformacja jednostki podłużnej εl jest odcinkiem podzielonym przez pierwotną długość:

εl = (l ' - l) / l

εl = (-14 mm) / 150 mm = -0,0933

Należy zauważyć, że podłużne jednolite deformacja jest bezwymiarowa, aw tym przypadku dało ujemne, ponieważ nastąpił spadek wymiaru podłużnego.

Rozwiązanie b

Podobnie jednolite odkształcenie poprzeczne εt jest zwężeniem promieniowym, podzielonym przez pierwotną średnicę:

εt = (d ' - d) / d

εT = (+0,85 mm) / 20 mm = 0,0425

Transversalne jednolite deformacja było pozytywne, ponieważ nastąpił wzrost średnicy baru.

Rozwiązanie c

Do obliczenia współczynnika Poissona musimy pamiętać, że jest on zdefiniowany jako ujemny iloraz między deformacją poprzeczną a deformacją wzdłużną:

ν = - εt / εl 

ν = - 0,0425 / (-0,0933) = 0,4554

Należy pamiętać, że współczynnik Poissona jest liczbą bezwymiarową, a dla większości materiałów wynosi od 0 do 0,5.

Może ci służyć: Darcy Law

Rozwiązanie d

Moduł elastyczności Younga, oznaczony literą E, jest stałą proporcjonalności w prawie Hooke. Poprzez E normalny wysiłek σl jest związany z jednolitym deformacją εl, jak następuje:

σl = e εl 

Normalny wysiłek jest definiowany jako iloraz między siłą normalną (w tym przypadku równolegle do osi paska) a przekroju:

σl = f / a = f / (π / 4 * d^2)

W tym wykonaniu Force F wynosi 612,25 kg-f, które zostaną wykonane dla Newtonów, które jest jednostką siły:

F = 612,25 kg-f = 612,25 * 9,8 n = 6000 n = 6 kN

Ze swojej strony przekrój A to:

A = (π/4 * d^2) = (31416/4) * (20 * 10^-3 m)^2 = 3 1416 * 10^-4 m^2

Wreszcie normalny wysiłek zastosowany do paska to:

σl = f / a = 6000 N / 3 1416 * 10^-4 m^2 = 19.098.593 PA = 19 098 MPa

Aby obliczyć moduł elastyczności Younga, oczyszczamy i prawa Hooke'a σl = e εl:

E = σl / εl = 19.098.593 PA / 0,0933 = 204,7 MPa

Rozwiązanie e

Moduł sztywności R jest związany z modułem Younga i współczynnikiem Poissona ν przez ten wzór:

E / (2 g) = 1 + ν 

Stamtąd możesz wyczyścić G:

G = E / (2 (1 + ν)) = 204,7 MPa / (2 (1 + 0,4554)) = 70,33 MPa

Przykład 2

Masz kabel o średnicy 4 mm i 1 m. Wiedząc, że moduł miedziany jest 110000 MPa i że jego współczynnik Poissona wynosi 0,34, szacuje o rozciąganiu i zwężenie, że drut cierpi, gdy ciężar 100 kg-f.

Rozwiązanie

Po pierwsze, konieczne jest obliczenie normalnego wysiłku trakcji, jaką waga wywiera na drut, zgodnie z tym wzorem:

Może ci służyć: wektory w przestrzeni: jak wykres, aplikacje, ćwiczenia

σl = f / a = f / (π / 4 * d^2)

Siła F wynosi 980 N, a przekrój to:

A = (π/4 * d^2) = (31416/4) * (4 * 10^-3 m)^2 = 1,2566 * 10^-5 m^2

Wtedy wysiłek trakcji jest:

σl = 980 N / 1 2566 * 10^-5 M^2 = 77.986.000 PA

Obliczanie jednolitego odkształcenia drutu

Moduł elastyczności Younga, oznaczony literą E, jest stałą proporcjonalności w prawie Hooke, która odnosi normalny wysiłek σl z jednolitym deformacją εl:

σl = e εl 

Stamtąd można usunąć podłużne jednolite odkształcenie drutu miedzianego:

εl = σl / e = 77 986 MPA / 110000 MPA = 7,09 * 10^-4

Obliczanie jednolitego odkształcenia poprzecznego

Z drugiej strony, aby poznać jednolite odkształcenie poprzeczne, zastosowano współczynnik Poissona:

ν = - εt / εl 

Wreszcie, musisz poprzecznie jednolite odkształcenie: 

εt = -ν εl = -0,34 * 7.09 * 10 ^-4 = -2,41 * 10 ^-4

KABLEJ bezwzględne obliczenia rozciągania

Wreszcie, aby poznać absolutne rozciąganie kabla, należy zastosować następujący związek:

ΔL = εl * l = 7,09 * 10^-4 * 1 M = 7,09 * 10^-4 M = 0,709 mm

To znaczy z tą wagą kabel ledwo rozciągnął 0,709 milimetrów.

Obliczenie spadku średnicy

Aby uzyskać absolutne kurczenie się o średnicy, używamy następującego wzoru:

ΔD = εT * d = -2,41 * 10 ^-4 * 4 mm = -9,64 * 10 ^-4 mm = -0 000964 milimetrów.

To zwężenie średnicy jest tak małe, że trudno docenić gołym okiem, nawet jego pomiar wymaga wysokiej precyzyjnej instrumentu.

Bibliografia

1. Piwo F ... mechanika materiałowa. 5. Wydanie. 2010. MC Graw Hill. 1-130.
2. Hibbeler R. Mechanika materiałów. Ósme wydanie. Prentice Hall. 2011. 3-60.
3. Gere J. Mechanika materiałów. Ósme wydanie. Cengage Learning. 4-220.
4. Giancoli, zm. 2006. Fizyka: zasady z aplikacjami. 6. edycja. Prentice Hall. 238-242.
5. Valera Negrete, J. 2005. Ogólne uwagi fizyki. Unam. 87-98.