Etapy cyklu Carnot, aplikacje, przykłady, ćwiczenia

On Cykl Carnot Jest to sekwencja procesów termodynamicznych, które mają miejsce w silniku Carnot, idealne urządzenie, które składa się tylko z procesów odwracalnych; to znaczy ci, którzy mieli miejsce, mogą powrócić do stanu początkowego.

Ten typ silnika jest uważany za idealny, ponieważ brakuje mu rozproszenia, tarcia lub lepkości, które powstają w prawdziwych maszynach, przekształcając energię cieplną w użyteczną pracę, chociaż konwersja nie jest przeprowadzana w 100%.

Rysunek 1. Lokomotywa parowa. Źródło: Pixabay

Silnik opiera się na substancji zdolnej do wykonywania pracy, takiej jak gaz, benzyna lub para. Ta substancja podlega różnym zmianom temperatury, a z kolei doświadcza zmian w jej ciśnieniu i objętości. W ten sposób można przesunąć tłok w cylindrze.

[TOC]

Jaki jest cykl Carnot?

Cykl Carnot odbywa się w systemie zwanym silnikiem Carnot lub C, który jest idealnym gazem zablokowanym w cylindrze i wyposażony w tłok, który jest w kontakcie z dwoma źródłami w różnych temperaturach t₁ oraz T₂ jak ten pokazany na poniższym rysunku po lewej stronie.

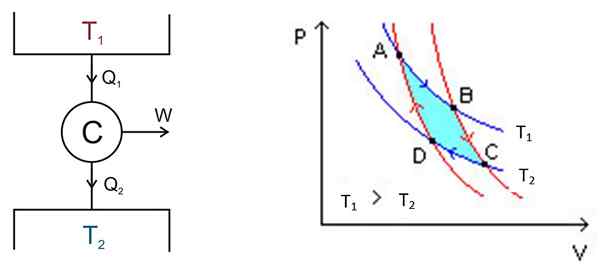Rysunek 2. Po lewej stronie schemat maszyny cnot, po prawej schemacie PV. Źródło lewego rysunku: Keta - Own Work, CC.5, https: // commons.Wikimedia.org/w/indeks.Php?Curid = 681753, prawe figura wikimedia Commons.

Istnieją następujące procesy w trybie szorstkim:

1. Do urządzenia dostarczana jest pewna ilość ciepła_wejście = Q₁ Ze zbiornika termicznego w wysokiej temperaturze t₁.
2. Silnik Carnot C wykonuje pracę w tym dostarczonym cieple.
3. Część używanego ciepła: odpady q_Wyjście, Jest przenoszony do zbiornika termicznego, który jest w niższej temperaturze t₂.

Etapy cyklu Carnot

Analiza jest przeprowadzana na podstawie diagramu p -V (ciśnienie -najemność), jak pokazano na ryc. 2 (prawy rysunek). Celem silnika może być utrzymanie zaczepu złoża termicznego 2, wydobywanie z niego ciepła. W tym przypadku jest to Maszyna czynnika chłodniczego. Jeśli wręcz przeciwnie, chcesz nadać ciepło depozyt termiczny 1, to jest to Pompa ciepła.

Schemat P -V pokazuje zmiany ciśnienia - temperatura silnika w dwóch warunkach:

- Utrzymanie stałej temperatury (proces izotermiczny).

- Brak transferu ciepła (izolacja termiczna).

Dwa procesy izotermiczne muszą być podłączone, co jest osiągane za pomocą izolacji termicznej.

Punkt

Możesz zacząć w dowolnym punkcie cyklu, w którym gaz ma określone warunki ciśnienia, objętości i temperatury. Gaz cierpi na serię procesów i może powrócić do warunków początkowych, aby rozpocząć kolejny cykl, a zawsze ostateczna energia wewnętrzna jest taka sama jak inicjał. Ponieważ energia jest zachowana:

Praca wykonana przez C = ciepło wejściowe - ciepło odlotu

ΔW = q_wejście - Q_Wyjście

Obszar zawarty w tym cyklu lub pętli, w turkusu na rysunku, jest dokładnie równy pracom wykonanym przez silnik Carnot.

Punkty A, B, C i D są oznaczone na rycinie 2. Zacznie się po punkcie śledzenia niebieskiej strzałki.

Pierwszy etap: ekspansja izotermiczna

Temperatura między punktami a i b wynosi t₁. System pochłania ciepło z depozytu termicznego 1 i cierpi rozszerzenie izotermiczne. Następnie objętość wzrasta, a ciśnienie maleje.

Jednak temperatura pozostaje w t₁, Od momentu, gdy gaz rozszerza się. Dlatego jego energia wewnętrzna pozostaje stała.

Może ci służyć: Graff Van Generator: Partie, jak to działa, aplikacje

Drugi etap: rozszerzenie adiabatyczne

W punkcie B system rozpoczyna nowe rozszerzenie, w którym system nie wygrywa ani nie traci ciepła. Osiąga się to poprzez umieszczenie go w izolacji kalorycznej, jak wskazano wcześniej. Dlatego jest to rozszerzenie adiabatyczne, które nadal wskaże C po czerwonej strzałce. Objętość wzrasta, a ciśnienie maleje, aż osiągnie najniższą wartość.

Trzeci etap: kompresja izotermiczna

Zacznij w punkcie C i zakończ w D. Izolacja jest usuwana, a system kontaktuje się z depozytem termicznym 2, którego temperatura t₂ To jest mniej. System daje ciepło odpadowe do zbiornika termicznego, ciśnienie zaczyna rosnąć, a objętość zmniejsza.

Czwarty etap: kompresja adiabatyczna

Dotarł do punktu D, system wraca do izolacji termicznej, ciśnienie wzrasta, a objętość spada, aż do osiągnięcia pierwotnych warunków punktu A. Następnie cykl powtarza się ponownie.

Twierdzenie Carnota

Twierdzenie Carnota zostało po raz pierwszy postulowane na początku XIX wieku przez francuskiego fizyka Sadi Carnota. W roku 1824 Carnot, który był częścią armii francuskiej, opublikował książkę, w której zaproponował odpowiedź na następujące pytanie: w jakich warunkach maszyna termiczna ma maksymalną wydajność? Następnie Carnot ustalił:

Brak silnika termicznego działającego między dwoma złożami termicznymi nie jest bardziej wydajny niż silnik Carnot.

Wydajność silnika termicznego jest podana przez stosunek między pracą W a pochłoniętym ciepłem q:

wydajność = praca wykonana/ciepło

W ten sposób wydajność dowolnego silnika termicznego I to: η = w/q. Podczas gdy wydajność silnika Carnot R wynosi η '= w/q', w przypadku obu silników są w stanie wykonać tę samą pracę.

Twierdzenie Carnota stwierdza, że ​​η nigdy nie jest większe niż η '. W przeciwnym razie jest sprzeczny z drugim prawem termodynamiki, zgodnie z którym proces, w którym wynik jest taki, że ciepło z korpusu niższej temperatury jest niemożliwe do przejścia do innej wyższej temperatury bez otrzymania pomocy zewnętrznej. Dlatego:

η _< η^'

Demonstracja twierdzenia Carnota

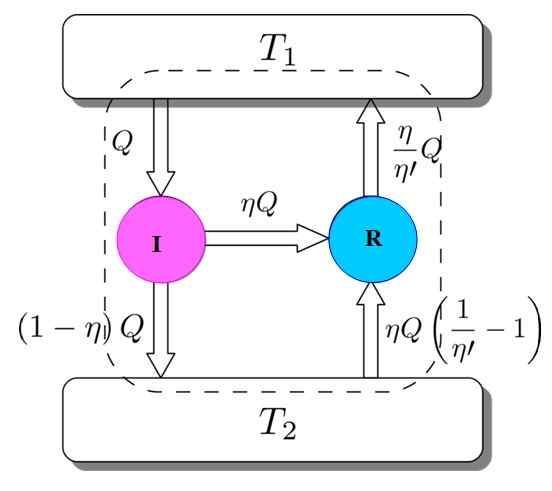
Aby pokazać, że tak jest, rozważ silnik Carnot działający jako maszyna do lodówki napędzana silnikiem I. Jest to możliwe, ponieważ silnik Carnot działa według odwracalnych procesów, jak określono na początku.

Rysunek 3. Demonstracja twierdzenia Carnota. Źródło: Netheril96 [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)]

Masz zarówno: ja i r pracujące z tym samym złóż termicznym i zostanie założone, że η _> η^'. Jeśli po drodze osiągnie sprzeczność z drugim prawem termodynamiki, twierdzenie Carnota jest wykazane przez zmniejszenie absurdu.

Rysunek 3 pomaga podążać za procesem. Silnik I przyjmuje ilość ciepła Q, co dzieli się w ten sposób: wykonywanie pracy na R równoważnym W = ηQ, a reszta to przeniesienie ciepła (1 -η) Q do zbiornika termicznego T₂.

Ponieważ energia jest zachowana, wszystko jest spełnione:

I_wejście = Q = praca w + ciepło przypisane do t₂ = ηq + (1 -η) q = e_Wyjście

Teraz maszyna do lodówki Carnot R pobiera zbiornik termiczny 2 ilość ciepła podana przez:

Może ci służyć: Imantacja: co polega na metodzie i przykładach

(η / η ') (1 -η') q =

W tym przypadku należy również zachować energię:

I_wejście = ηq + (η / η ') (1 -η') q = (η / η ') q = q' = e_Wyjście

Rezultatem jest przeniesienie do zbiornika termicznego t₂ ilości ciepła podanego przez (η / η ') q = q'.

Jeśli η jest większe niż η 'oznacza to, że złożenie termiczne o najwyższej temperaturze przyniosło więcej ciepła niż pierwotnie wziąłem. Ponieważ nie uczestniczył żaden środek zewnętrzny, taki jak inne źródło termiczne, jedynym sposobem, w jaki mogłoby się to zdarzyć, jest to, że najzimniejszy depozyt termiczny daje ciepło.

Nie zgadza się z drugim prawem termodynamiki. Stwierdzono zatem, że nie jest możliwe, że η^' Być mniej niż η, dlatego silnik I nie może mieć większej wydajności niż maszyna Carnot R.

Twierdzenie następstwa i ograniczenia

W następstwie Carnot Twierdzenie stwierdza, że ​​dwie maszyny Carnot mają taką samą wydajność, jeśli obie działają z tym samym złóż termicznym.

Oznacza to, że substancja nie ma znaczenia, wydajność jest niezależna i nie można jej podnieść, zmieniając ją.

Wniosek z poprzedniej analizy jest taki, że cykl Carnota jest szczytem idealnie osiągalnego procesu termodynamicznego. W praktyce istnieje wiele czynników, które zmniejszają wydajność, na przykład fakt, że izolacja nigdy nie jest doskonała, aw stadiach adiabatycznych w rzeczywistości istnieje wymiana kaloryczna z zewnętrzną częścią.

W przypadku samochodu blok silnika jest podgrzewany. Z drugiej strony mieszanka gazu i powietrza nie zachowuje się dokładnie jako gaz idealny, który jest punktem wyjścia cyklu Carnota. To wspomina tylko niektóre czynniki, które spowodują drastyczną redukcję wydajności.

Przykłady

Tłok w cylindrze

Jeśli system jest tłokiem zablokowanym w cylindrze, jak na rycinie 4, tłok wznosi się podczas ekspansji izotermicznej, jak widać w pierwszym schemacie ekstremalnej lewicy, a także wznosi się podczas rozszerzenia adiabatycznego.

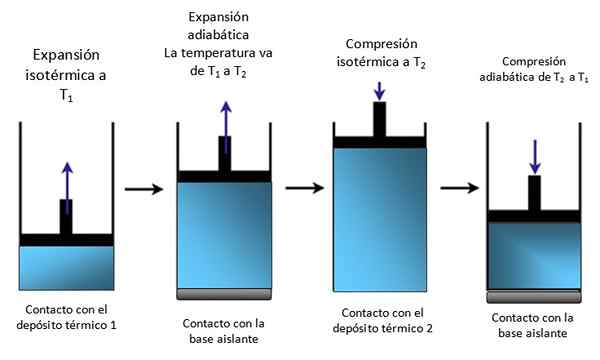Rysunek 4. Ruch tłoka w cylindrze. Źródło: Self Made.

Następnie izotermicznie ściskane, dając ciepło i nadal kompresuje adiabatycznie. Rezultatem jest ruch, w którym tłok wznosi się i w dół wewnątrz cylindra i może być przesyłany na inne części konkretnego urządzenia, takie jak na przykład silnik samochodowy, który wytwarza parę lub parną maszynę.

Różne odwracalne procesy

Oprócz ekspansji i kompresji gazu idealnego wewnątrz cylindra istnieją inne idealne odwracalne procesy, z którymi można skonfigurować cykl Carnot, na przykład:

- Ruchy w obie strony przy braku tarcia.

- Idealna sprężyna, która jest ściśnięta i dekompresowana, a to nigdy nie jest deforma.

- Obwody elektryczne, w których nie ma oporu, który rozprasza energię.

- Cykle magnetyzacji i demagnetyzacji, w których nie ma strat.

- Ładowanie i pobieranie baterii.

Elektrownia jądrowa

Chociaż jest to bardzo złożony system, następuje pierwsze podejście do produkcji energii w reaktorze jądrowym:

- Źródło termiczne, składające się z materiału, który rozpada się radiowo -uranu.

Może ci służyć: obecny model atomowy

- Zlew lub zimny depozyt termiczny, który byłby atmosfera.

- „Maszyna Carnot”, która wykorzystuje płyn, prawie zawsze bieżącą wodę, który jest dostarczany ciepło ze źródła termicznego, aby zamienić ją w parę.

Po przeprowadzeniu cyklu, energia elektryczna jest uzyskiwana jako praca netto. Po przekształceniu w parę o wysokiej temperaturze woda dochodzi do turbiny, gdzie energia jest przekształcana w ruch lub energię kinetyczną.

Turbina z kolei aktywuje generator elektryczny, który przekształca energię jego ruchu w energię elektryczną. Oprócz materiałów do pięści, takich jak uran, oczywiście paliwa kopalne mogą być stosowane jako źródło ciepła.

Rozwiązane ćwiczenia

-Przykład 1: Wydajność maszyny termicznej

Wydajność maszyny termicznej jest definiowana jako stosunek pracy wyjściowej a pracą wejściową, a zatem jest ilością bezwymiarową:

Maksymalna wydajność = (q_wejście - Q _Wyjście) /Q_wejście

Oznaczanie maksymalnej wydajności jako e_Max, Możliwe jest wykazanie zależności temperatury, która jest najłatwiejszą zmienną do pomiaru, na przykład:

I_Max = 1 - (t₂/T₁)

Gdzie t₂ Jest to temperatura zlewu i t₁ Jest to temperatura źródła termicznego. Ponieważ te ostatnie jest większe, wydajność zawsze okazuje się mniej niż 1.

Załóżmy, że maszyna termiczna jest w stanie pracować nad następującymi sposobami: a) między 200 k do 400 K, b) między 600 K do 400 K. Jaka jest wydajność w każdym przypadku?

Rozwiązanie

a) W pierwszym przypadku wydajność wynosi:

I_MAX1 = 1 - (200/400) = 0.pięćdziesiąt

b) W drugim trybie wydajność będzie:

I_MAX2 = 1- (400/600) = 0.33

Chociaż różnica temperatur jest taka sama między obiema trybami, wydajność nie jest. A jeszcze bardziej godne uwagi jest to, że najbardziej wydajny tryb działa w niższej temperaturze.

-Przykład 2: Absorbowane ciepło i ciepło Ceded

Maszyna termiczna w wysokości 22 % produkuje 1530 J pracy. Znajdź: a) Ilość ciepła pochłoniętego z złoża termicznego 1, b) Ilość ciepła odrzuconego do zbiornika termicznego 2.

a) W tym przypadku stosowana jest definicja wydajności, ponieważ wykonana praca nie jest dostępna temperatury depozytów termicznych. 22% wydajność oznacza, że ​​e _Max = 0.22 Dlatego:

Maksymalna wydajność = praca /q_wejście

Ilość pochłoniętego ciepła jest dokładnie Q_wejście, Więc czyszczysz:

Q_wejście = Praca/wydajność = 1530 J/0.22 = 6954.5 J

b) Ilość ciepła przypisanego do najzimniejszego zbiornika wynosi δW = q_wejście - Q_Wyjście

Q_Wyjście = Q_wejście - ΔW = 6954.5 -1530 J = 5424.5 J.

Inny sposób jest z I_Max = 1 - (t₂/T₁). Ponieważ temperatury nie są znane, ale są one związane z ciepłem, wydajność można również wyrazić jako:

I_Max = 1 - (Q_Sceding/Q_{zaabsorbowany})

Bibliografia

1. Bauer, w. 2011. Fizyka inżynierii i nauki. Tom 1. MC Graw Hill. 654-657
2. Energia nuklearna. Działanie elektrowni jądrowej. Odzyskane z: energetyka-nuklear.internet
3. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning. 618-622.
4. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. MacGraw Hill. 414-416.
5. Walker, J.2008. Fizyka. Czwarty edycja.Addison Wesley. 610-630