Nieelastyczne starcia w wymiarze i przykładach

Nieelastyczne wstrząsy lub nieelastyczne zderzenia są krótką i intensywną interakcją między dwoma obiektami, w których zachowana jest ilość ruchu, ale nie energia kinetyczna, z której procent jest przekształcany w inny rodzaj energii.

Wstrząsy lub zderzenia mają charakter. Cząstki subatomowe zderzają się z bardzo dużą prędkością, podczas gdy wiele sportów i gier składa się z ciągłych zderzeń. Nawet galaktyki są zdolne do zderzenia.

Rysunek 1. Zderzenie samochodu testowego. Źródło: Pixabay

W rzeczywistości ilość ruchu jest zachowana w każdym rodzaju kolizji, o ile cząstki zderzyły się przez izolowany system. Więc w tym sensie nie ma problemu. Teraz obiekty mają energię kinetyczną związaną z ruchem, który mają. Co może się zdarzyć z tą energią podczas awarii?

Siły wewnętrzne, które mają miejsce podczas starcia między obiektami, są intensywne. Kiedy stwierdzono, że energia kinetyczna nie jest zachowana, oznacza to, że jest przekształcana w inne rodzaje energii: na przykład w energii dźwiękowej (zderzenie urządzenia ma charakterystyczny dźwięk).

Więcej możliwości wykorzystania energii kinetycznej: ciepło przez tarcie i oczywiście nieuniknione odkształcenie cierpiące przez obiekty podczas zderzenia, takie jak ciała samochodu na powyższym rysunku.

[TOC]

Przykłady nieelastycznych zderzeń 

- Dwie masy plastyny, które zderzają się i spotykają razem, poruszając się jak jeden kawałek po katastrofie.

- Gumowa kulka, która podskakuje o ścianę lub podłogę. Piłka deformuje się podczas wpływu na powierzchnię.

Nie cała energia kinetyczna jest przekształcana w inne rodzaje energii, z wyjątkiem kilku wyjątków. Obiekty mogą pozostać z pewną ilością tej energii. Później zobaczymy, jak obliczyć procent.

Kiedy elementy zderzane są połączone, kolizja nazywa się idealnie nieelastyczną i oba zwykle kończą się razem.

Doskonale nieelastyczne zderzenia w wymiarze

Zderzenie figury pokazuje dwa obiekty różnych mas M₁ I M₂, poruszanie się do siebie z prędkością v_i1 I v_I2 odpowiednio. Wszystko dzieje się na poziomie, to znaczy jest zderzeniem w wymiarze, najprostszym do nauki.

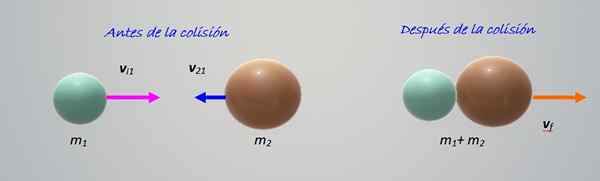Rysunek 2. Zderzenie między dwiema cząstkami różnych mas. Źródło: Self Made.

Obiekty zderzają się, a następnie są zjednoczone, przesuwając się w prawo. Jest to doskonale nieelastyczna kolizja, więc wystarczy, abyśmy zachowały ilość ruchu:

P_albo = P_F

Ilość ruchu to wektor, którego jednostki to n.S. W opisanej sytuacji zapis wektorowy można wydać, ponieważ jest to zderzenia w wymiaru:

Może ci służyć: Easy Physics Experiments (pierwotna uniwersytet)

Mv_albo = mv_F

Ilość ruchu układu jest wektorową sumą ilości ruchu każdej cząstki.

M₁ v_i1  + M₂ v_I2 = (m₁ + M₂) v_F

Ostateczna prędkość jest podana przez:

v_F = (m₁ v_i1  + M₂ v_I2)/ (M₁ + M₂)

Współczynnik restytucji

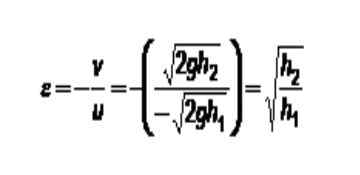
Istnieje kwota, która może wskazać, jak elastyczna jest kolizja. To jest o Współczynnik restytucji, który jest zdefiniowany jako ujemny stosunek między względną prędkością cząstek po awarii a prędkością względną przed awarią.

Pozwolę ci₁ i Ty₂ Odpowiednie prędkości cząstek początkowo. I bądź v₁ i v₂ odpowiednie końcowe prędkości. Matematycznie współczynnik zwrotu można wyrazić w następujący sposób:

Współczynnik restytucji jest dodatkową ilością, ponieważ jest to stosunek między prędkością. Ale podane informacje są bardzo interesujące:

- Jeśli ε = 0 jest równoważne stwierdzeniem, że v₂ = v₁. Oznacza to, że końcowe prędkości są takie same, a starcie jest nieelastyczne, jak opisano w poprzednim rozdziale.

- Gdy ε = 1 oznacza, że ​​prędkość względna zarówno przed, jak i po awarii się nie zmienia, w tym przypadku zderzenie jest sprężyste.

- I jeśli 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Jak określić współczynnik zwrotu?

Współczynnik restytucji zależy od klasy materiałów zaangażowanych w kolizję. Bardzo interesującym testem do ustalenia, w jaki sposób elastyczna jest materiałem do wykonania piłek, jest upuszczenie piłki na stałej powierzchni i mierzenie wysokości odbicia.

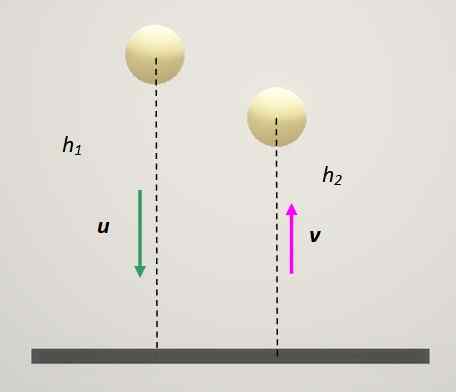Rysunek 3. Metoda określenia współczynnika zwrotu. Źródło: Self Made.

W tym przypadku stała płyta zawsze ma prędkość 0. Jeśli ten indeks 1 jest przypisany do tego, a piłka to: indeks 2 pozostaje:

Początkowa prędkość zależy od wysokości H₁ z którego upuścił:

Znak ujemny wskazuje w dół kierunku. A końcowa prędkość jest związana z maksymalną wysokością H₂ To sięga w odbiciu:

Zastąpienie współczynnika zwrotu:

Eksplozje

Na początku zasugerowano, że całą energię kinetyczną można przekształcić, przechodząc do innych rodzajów energii. W końcu energia nie jest niszczona. Czy to możliwe, że obiekty, które pojawiły się wraz z ruchem, zderzają się i łączą, tworząc jeden obiekt, który nagle odpoczywa? To nie jest takie proste do wyobrażenia.

Może ci służyć: dynamika: historia, jakie studia, prawa i teorie

Wyobraźmy sobie jednak, co się stanie do tyłu, jak w filmie widocznym z tyłu. Następnie obiekt początkowo odpoczywał, a następnie eksploduje fragmentowanie w kilka części. Ta sytuacja jest całkowicie możliwa: jest to eksplozja.

Tak aby eksplozja mogła być traktowana jako idealnie nieelastyczna zderzenie postrzegane do tyłu w czasie. Ilość ruchu jest również zachowana, będąc w stanie potwierdzić:

P_albo = P_F

Rozwiązane przykłady

-Ćwiczenie 1

Z pomiarów wiadomo, że współczynnik restytucji stali wynosi 0.90. Stalowa kula jest upuszczana z 7 m wysokości na stałej płycie. Oblicz:

a), dopóki wzrost będzie się odbity.

b) Ile trwa między pierwszym kontaktem z powierzchnią a drugim.

Rozwiązanie

a) Zastosowane jest równanie, które wcześniej wydedukowano w sekcji dotyczącej określenia współczynnika zwrotu:

Wysokość oczyszcza H₂:

0.90² . 7 m = 5.67 m

b) podnieść 5.67 metrów prędkość podana przez:

Skąd:

A czas potrzebny na osiągnięcie tej wysokości to:

T _Max = v_albo/ g = (10.54/9.8 s) = 1.08 s.

Czas potrzebny na powrót jest taki sam, dlatego całkowity czas na przesłanie 5.67 metrów i powrót do punktu początkowego jest dwa razy więcej niż maksymalny czas:

T_lot = 2.15 s.

-Ćwiczenie 2

Rysunek pokazuje blok drewna masy m wiszący w pozostałej części nici długości L jako wahadło. Nazywa się to wahadłem balistycznym i służy do pomiaru prędkości v wejścia Mass masy m. Im wyższa prędkość, z jaką kula wpływa na blok, na wyższej wysokości h zostanie zbudowane.

Kula obrazu jest osadzona w bloku, dlatego jest to całkowicie nieelastyczny wstrząs.

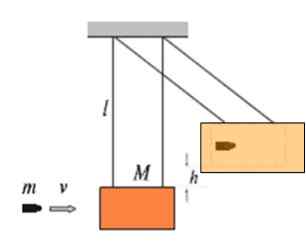Rysunek 4. Balistyczne wahadło.

Załóżmy, że A 9 9.72 g Wpływ na Mass Block 4.60 kg, potem zestaw wzrasta do 16.8 cm pozycji równowagi. Jaka jest prędkość v kuli?

Rozwiązanie

Podczas kolizji ilość ruchu jest zachowana i Lub_F Jest to prędkość zestawu, gdy kula zostanie osadzona w bloku:

P_albo = P_F

Blok początkowo odpoczywa, a kula jest skierowana do celu z prędkością v:

M.V + m.0 = (m + m) u_F

 

Nie jest znane Lub_F Nawet, ale po zderzeniu zachowuje się energię mechaniczną, jest to suma grawitacyjnej energii potencjalnej i energii kinetycznej k:

Może ci służyć: suma wektorów: metoda graficzna, przykłady, rozwiązane ćwiczenia

Początkowa energia mechaniczna = końcowa energia mechaniczna

I_mo = E_MF

LUB_albo + K_albo = U_F + K_F

Grawitacyjna energia potencjalna zależy od wysokości, na której osiąga zestaw. Dla pozycji równowagi wysokość początkowa jest zatem przyjęta jako poziom odniesienia:

LUB_albo = 0

Dzięki kuli zestaw ma energię kinetyczną K_albo, który staje się grawitacyjną energią potencjalną, gdy zestaw osiągnie maksymalną wysokość H. Energia kinetyczna jest podana przez:

K = ½ mV²

Początkowo energia kinetyczna to:

K_albo = (1/2) (m+m) u_F²

Pamiętaj, że kula i blok tworzą jeden obiekt masy M+ m. Grawitacyjna energia potencjalna, gdy osiągną maksymalną wysokość, wynosi:

LUB_F = (M + m) GH

Dlatego:

K_albo = U_F

(1/2) (m+m) u_F² = (M + m) GH

Teraz ten wynik jest zastępowany w wyrażeniu v które oczyszczały się na początku, z ochrony ilości ruchu:

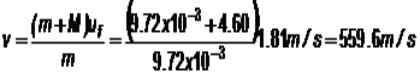
-Ćwiczenie 3

Obiekt figury eksploduje w trzech fragmentach: dwóch o równej masie M i jednej większej masie 2M. Rysunek wskazuje prędkości każdego fragmentu po eksplozji. Jaki był początkowy cel obiektu?

Rysunek 5. Kamień, który eksploduje w 3 fragmentach. Źródło: Self Made.

Rozwiązanie

Ten problem wymaga użycia dwóch współrzędnych: X I I, Ponieważ dwa fragmenty mają prędkości pionowe, a pozostałe mają prędkość poziomą.

Całkowita masa obiektu jest sumą masy wszystkich fragmentów:

M = M + M + 2M = 4M

Ilość ruchu jest zachowana zarówno na osi x, jak i na osi y, jest proponowany osobno:

1. 4M. Lub_X= m v₃
2. 4M. Lub_I = m. 2v₁ - 2M. v₁

Zauważ, że duży fragment porusza się w dół z prędkością V1, aby wskazać ten fakt, że został umieszczony znak ujemny.

Z drugiego równania natychmiast następuje to Lub_I = 0, I pierwszy jest natychmiast wyraźny UX:

Pierwszym celem obiektu był u_albo = u_X = v₃/4.

Bibliografia

1. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6^th. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Podstawy fizyki. osoba. 135-155.
3. Serway, r., Vulle, c. 2011. Podstawy fizyki. 9^na Cengage Learning. 172-182
4. Tipler, str. (2006) Physics for Science and Technology. Ed. Tom 1. Redakcja Reverted. 217-238
5. Tippens, s. 1. 2011. Fizyka: koncepcje i zastosowania. 7. edycja. MacGraw Hill. 185-195