Kwoty wektora

Jakie są kwoty wektorowe?

Wielkość wektorowa, lub wektor, jako taki, dla którego konieczne jest określenie zarówno jego wielkości, jak i modułu (z odpowiednimi jednostkami), jak i ich adresem.

W przeciwieństwie do ilości wektorowej ilość skalarna ma tylko wielkość (i jednostki), ale nie adres. Niektóre przykłady wielkości skalarnych są między innymi temperatura, objętość obiektu, długość, masa i czas.

Różnica między ilością wektora a wspinaczką

W poniższym przykładzie możesz nauczyć się odróżniać ilość skalarnego od ilości wektorowej:

Prędkość 10 km/h to ilość skalarna, a prędkość 10 km/h na północ to ilość wektorowa. Różnica polega na tym, że w drugim przypadku określono adres, oprócz wielkości.

Ilości wektorowe mają nieskończoność zastosowań, szczególnie w świecie fizyki.

Grafika i denotacje ilości wektorowej

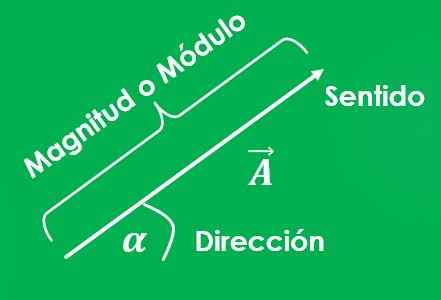
Sposób oznaczenia kwoty wektora jest umieszczenie strzałki (→) na liście do użycia lub pisanie listu z pogrubionym (Do).

Aby wykresować ilość wektorową, potrzebny jest system odniesienia. W takim przypadku płaszczyzna kartezjańska będzie używana jako system referencyjny.

Wykres wektora jest linią, której długość reprezentuje wielkość; a kąt między wspomnianą linią a osą X, mierzoną w sensie antyhorarycznym, reprezentuje swój adres.

Należy określić, jaki jest punkt początkowy wektora i jaki jest punkt przybycia. Strzałka jest również umieszczana na końcu linii, która wskazuje do punktu przybycia, co wskazuje, jaki jest kierunek wektora.

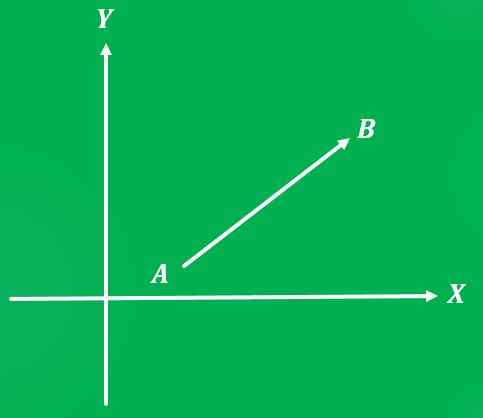
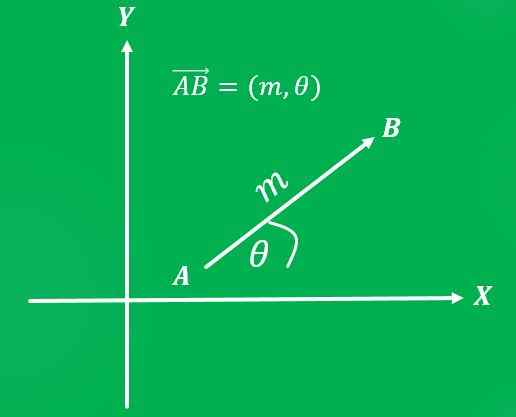
Po ustawieniu systemu odniesienia możesz napisać wektor jako parę uporządkowaną: pierwsza współrzędna reprezentuje jego wielkość, a druga współrzędna jego adres.

Przykłady kwot wektorowych

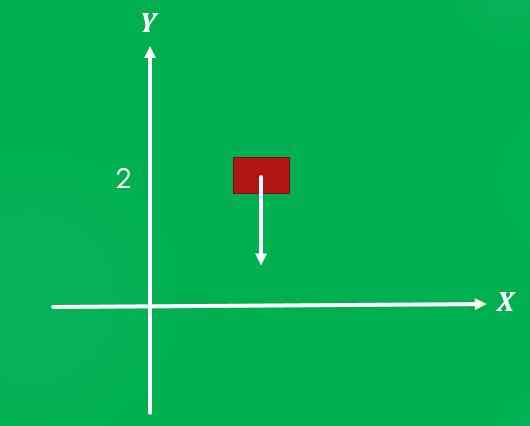
1- grawitacja działająca na obiekcie

Jeśli obiekt jest umieszczony na wysokości 2 metrów nad ziemią i jest zwolniony, grawitacja działa na nim o wielkości 9,8 m/s² i kierunku prostopadle do ziemi w kierunku.

2- Ruch płaszczyzny

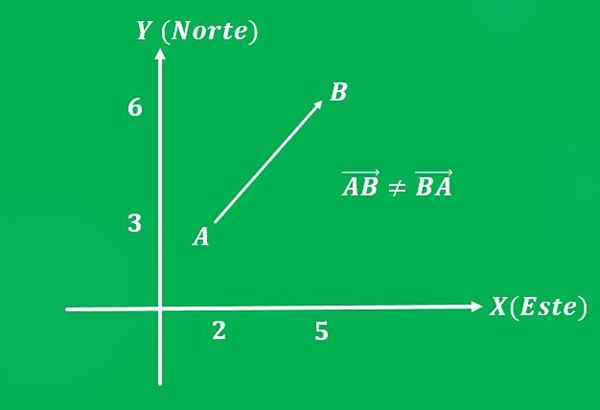
Płaszczyzna, która przeniesiona z punktu A = (2,3) do punktu B = (5,6) płaszczyzny kartezjańskiej, z prędkością 650 km/h (wielkość). Kierunek trajektorii wynosi 45 ° na północny wschód (znaczenie).

Należy zauważyć, że jeśli zamówienie jest odwrócone, wektor ma tę samą wielkość i ten sam kierunek, ale inne znaczenie, które będzie na południowy zachód.

3- siła zastosowana do obiektu

Juan postanawia pchnąć krzesło z siłą 10 funtów, w kierunku równolegle do ziemi. Możliwe zmysły przyłożonej siły to: po lewej lub prawej stronie (w przypadku płaszczyzny kartezjańskiej).

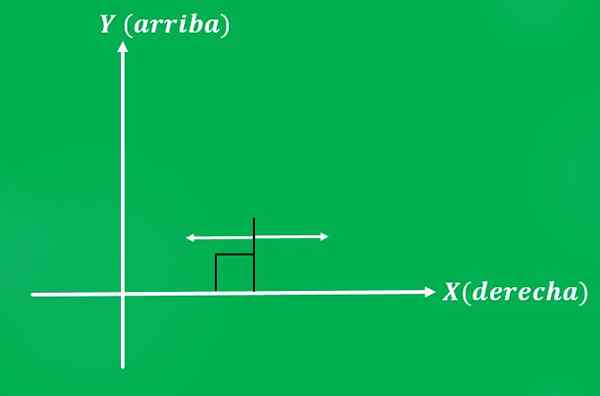
Podobnie jak w poprzednim przykładzie, znaczenie, które Juan postanawia podać siłę, przyniesie inny wynik.

To mówi nam, że dwa wektory mogą mieć tę samą wielkość i kierunek, ale być różne (daj różne wyniki).

Można dodać i odejmować dwa lub więcej wektorów, dla których są bardzo przydatne wyniki, takie jak prawo równoległoboku. Możesz także pomnożyć wektor przez skalar.