Koncepcja bezpłatnej koncepcji, równania, ćwiczenia rozwiązane

Freefall Jest to ruch pionowy, którego obiekt doświadcza, gdy jest upuszczony z pewnej wysokości w pobliżu powierzchni ziemi. Jest to jeden z najprostszych i najbardziej bezpośrednich ruchów, które są znane: w linii prostej i ze stałym przyspieszeniem.

Wszystkie obiekty, które są upuszczane lub są rzucane pionowo w górę lub w dół, poruszają się z przyspieszeniem 9.8 m/s² dostarczone przez nasilenie ziemi, niezależnie od jej masy.

Wolny upadek z klifu. Źródło: Pexels.com.

Fakt ten może zostać zaakceptowany dzisiaj bez problemów. Jednak zrozumienie prawdziwej natury wolnego upadku trwało trochę czasu. Grecy już to opisali i interpretowali bardzo zasadniczo w czwartym wieku A C.

[TOC]

Równania ruchu wolnego upadku

Kiedyś przekonany, że przyspieszenie jest takie samo dla wszystkich ciał zwolnionych pod działaniem grawitacji, nadszedł czas, aby ustalić niezbędne równania, aby wyjaśnić ten ruch.

Ważne jest, aby podkreślić, że opór powietrza nie jest brany pod uwagę w tym modelu pierwszego ruchu. Jednak wyniki tego modelu są bardzo precyzyjne i bliskie rzeczywistości.

We wszystkim, co następuje, model cząstek będzie przypuszczalny, to znaczy wymiary obiektu nie są brane pod uwagę, zakładając, że cała masa jest skoncentrowana w jednym punkcie.

W przypadku jednolicie przyspieszonego ruchu prostoliniowego jest on traktowany jako oś odniesienia do osi i. Pozytywny sens jest pobierany, a negatywny.

Kinematyczne wielkości

W ten sposób równania pozycji, prędkość i przyspieszenie w zależności od czasu to:

Przyśpieszenie

A = g = -9.8 m/s² (-32 stóp/s²)

Pozycja w zależności od czasu: oraz T)

y = y_albo + v_albo . T + ½ gt²

Gdzie i_albo Jest to początkowa pozycja telefonu komórkowego i v_albo to początkowa prędkość. Pamiętaj, że w pionowym uruchomieniu prędkość początkowa koniecznie różni się od 0.

Można to napisać jako:

i i_albo = v_albo . T + ½ gt²

ΔY = v_albo . T + ½ gt²

Z δI będąc przemieszczeniem wykonanym przez cząsteczkę mobilną. W jednostkach systemu międzynarodowego zarówno pozycji, jak i przemieszczenia podano w metrach (M).

Prędkość w zależności od czasu: V (t)

v = v_albo + G . T

Prędkość w zależności od przesunięcia

Możliwe jest wydukanie równania, które łączy przemieszczenie z prędkością, bez czasu interweniowania czasu. Aby to zrobić, czas ostatniego równania jest oczyszczony:

Może ci służyć: kwantowy model mechaniczny atomu

 I jest zastępowany w równaniu przemieszczenia:

ΔY = v_albo . T + ½ gt²

Plac jest opracowywany za pomocą niezwykłego produktu, a terminy są przegrupowane.

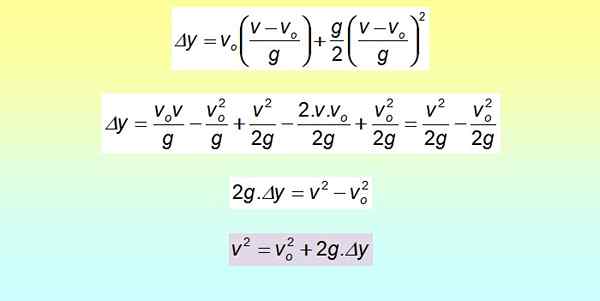
To równanie jest przydatne, gdy czas nie jest dostępny, ale zamiast tego istnieją prędkości i przemieszczenia, jak widać w części rozstrzygniętych przykładów.

Przykłady wolnego upadku

Uważny czytelnik zauważy obecność początkowej prędkości v_albo. Poprzednie równania są ważne dla ruchów pionowych pod działaniem grawitacji, zarówno gdy obiekt spadnie z pewnej wysokości, tak jakby został wyrzucony w górę lub w dół.

Kiedy obiekt upadnie, po prostu jest to zrobione v_albo = 0 a równania są uproszczone w następujący sposób.

Przyśpieszenie

A = g = -9.8 m/s² (-32 stóp/s²)

Pozycja w zależności od czasu: oraz T)

y = y_albo+ ½ Gt²

Prędkość w zależności od czasu: V (t)

v = g . T

Prędkość w zależności od przesunięcia

v² = 2G. Dy

Dy Będzie to również negatywne v² To musi być dodatnia kwota. Stanie się to zarówno, jeśli pochodzenie albo zero systemu współrzędnych w punkcie uruchomienia lub na ziemi.

Jeśli czytelnik go woli, może przenieść kierunek w dół jako pozytywny. Grawitacja będzie nadal działać, jeśli jest uważane za to, że jest to + 9.8 m/s². Ale musisz być spójny z konwencją wybranych znaków.

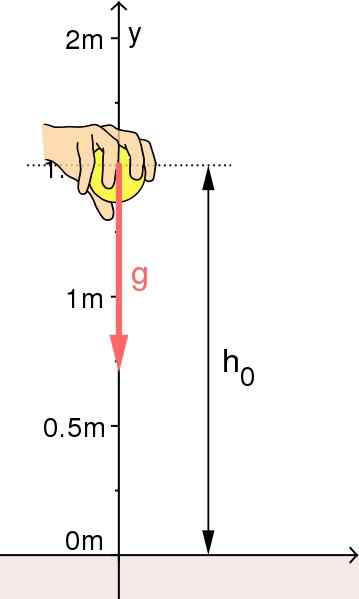Wolny upadek obiektu: Pochodzenie systemu odniesienia zostało wybrane na ziemi. Źródło: Źródło: Mikerun [CC BY-SA 4.0 (https: // creativeCommons.Org/licencje/nabrzeże/4.0)]

Pionowe start

Tutaj oczywiście początkowa prędkość nie może być zerowa. Musimy podać obiekt dla impulsu, aby wzrosnąć. Zgodnie z zapewnioną początkową prędkością obiekt wzrośnie do większej lub mniejszej wysokości.

Oczywiście będzie moment, w którym obiekt na chwilę się zatrzymuje. Wówczas maksymalna wysokość zostanie osiągnięta w odniesieniu do punktu uruchomienia. Również przyspieszenie jest nadal w dół. Zobaczmy, co się stanie w tym przypadku.

Obliczanie maksymalnej wysokości osiągniętej

Wybór mnie = 0:

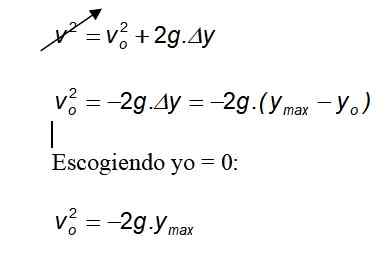
Ponieważ grawitacja zawsze wskazuje na ziemię w kierunku ujemnym, znak ujemny jest anulowany.

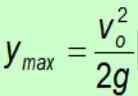
Maksymalne obliczenia czasu

Podobna procedura służy znalezieniu czasu potrzebnego do osiągnięcia obiektu na maksymalną wysokość.

v = v_albo + G . T

To robi v = 0

v_albo = - g . T_Max

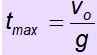
Czas lotu to czas, w którym obiekt trwa w powietrzu. Jeśli obiekt powróci do punktu początkowego, czas wzrostu jest równy czasowi zejścia. Dlatego czas lotu to 2. T Max.

Może ci służyć: Skala mikroskopowa: właściwości, cząstki zliczania, przykłady

Jest dwa razy więcej_Max Całkowity czas, jaki obiekt trwa w powietrzu? Tak, dopóki obiekt zaczyna się od punktu i wraca do niego.

Jeśli uruchomienie zostanie wykonane z określonej wysokości na ziemi, a obiekt może kontynuować, czas lotu nie będzie już dwa razy więcej niż maksymalny czas.

Rozwiązane ćwiczenia

W rozwiązywaniu następujących ćwiczeń zostanie rozważone następujące:

1-Wysokość z miejsca upuszczenia obiektu jest niewielka w porównaniu do promienia ziemi.

2-Odporność na powietrze jest nikczemna.

3-Wartość przyspieszenia grawitacji wynosi 9.8 m/s²

4--gdy jest to problemy z jednym telefonem komórkowym, najlepiej jest wybrany i_albo = 0 w punkcie początkowym. To zwykle ułatwia obliczenia.

5-mniejsze niż odwrotnie jest wskazane, kierunek w górę jest uznawany za dodatni.

6 -W łącznych ruchach rosnących i zstępujących równania bezpośrednio oferują prawidłowe wyniki, o ile spójność jest utrzymywana z znakami: Up pozytywnie, w dół negatywnej i nasilenia -9.8 m/s² lub -10 m/s² Jeśli wolisz okrążyć (dla większego wygody podczas obliczania).

Ćwiczenie 1

Piłka jest rzucana w pionowo z prędkością 25.0 m/s. Odpowiedz na następujące pytania:

a) Ile to rośnie?

b) Ile czasu zajmuje osiągnięcie najwyższego punktu?

c) Jak długo trwa piłka, aby dotknąć powierzchni ziemi po osiągnięciu jej najwyższego punktu?

d) Jaka jest twoja prędkość, gdy wrócisz do poziomu, w którym się zaczął?

Rozwiązanie

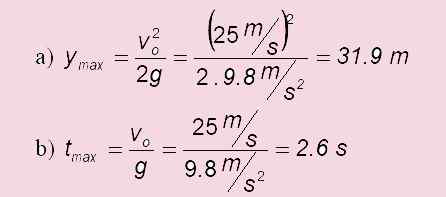
c) W przypadku uruchomienia poziomu: T_lot = 2 . T_Max = 2 x6 s = 5.1 s

d) Gdy powróci do punktu początkowego, prędkość ma taką samą wielkość jak prędkość początkowa, ale przeciwny kierunek, dlatego musi być - 25 m/s. Można go łatwo sprawdzać, zastępując wartości w równaniu dla prędkości:

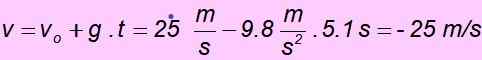
Ćwiczenie 2

Mała walizka pocztowa jest uwalniana z helikoptera, która schodzi ze stałą prędkością 1.50 m/s. Po 2.00 s Oblicz:

a) Jaka jest prędkość walizki?

b) Jak daleko jest walizka pod helikopterem?

c) Jakie są twoje odpowiedzi na sekcje a) i b) Jeśli helikopter wzrasta ze stałą prędkością 1.50 m/s?

Rozwiązanie

Sekcja A

Porzucając helikopter, walizka ma zatem jej początkową prędkość v_albo = -1.50 m/s. Z wskazanym czasem prędkość wzrosła dzięki przyspieszeniu grawitacji:

Może ci służyć: ciała niebieskie

v = v_albo + G . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Sekcja b

Zobaczmy, jak bardzo walizka opadła w odniesieniu do punktu początkowego w tym czasie:

Walizka: Dy = v_albo . T + ½ gt² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Został wybrany I_albo = 0 W punkcie początkowym, jak wskazano na początku sekcji. Znak ujemny wskazuje, że walizka zstąpiła 22. 6 m poniżej punktu początkowego.

Tymczasem helikopter Upadł szybko -1.50 m/s, zakładamy stale, dlatego we wskazanym czasie 2 sekund helikopter podróżował:

Helikopter: δy = v_albo.t = -1.pięćdziesiąt x 2 m = -3 m.

Dlatego po 2 sekundach walizka i helikopter są oddzielone odległością od:

D =|. -22.6 - (-3) |. M = 19. 6 m.

Odległość jest zawsze pozytywna. Aby podkreślić ten fakt, stosowana jest wartość bezwzględna.

Sekcja c

Kiedy helikopter wzrasta, ma prędkość + 1.5 m/s. Z tą prędkością wychodzi walizka, więc po 2 s już niesie:

v = v_albo + G . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

Prędkość okazuje się ujemna, ponieważ po 2 sekundach walizka się spada w dół. Zwiększył się dzięki grawitacji, ale nie tak bardzo, jak w sekcji A.

Teraz przekonamy się, jak bardzo walizka zstąpiła w odniesieniu do punktu początkowego podczas pierwszych 2 sekund podróży:

VALIJA: δy = v_albo . T + ½ gt² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Tymczasem helikopter Wzrosło Jeśli chodzi o punkt początkowy i zrobił to ze stałą prędkością:

Helikopter: δy = v_albo.T = +1.pięćdziesiąt x 2 m = +3 m.

Po 2 sekundach walizka i helikopter są oddzielone odległością od:

D =|. -16.6 - (+3) |. M = 19.6 m

Odległość, która je oddziela, jest taka sama w obu przypadkach. Walizka przemieszcza mniej pionową odległość w drugim przypadku, ponieważ jej początkowa prędkość była skierowana w górę.

https: // youtu.BE/W2UVETXWSFK

Bibliografia

1. Kirkpatrick, L. 2007. Fizyka: spojrzenie na świat. 6^ta Skrócone wydanie. Cengage Learning.  23 - 27.
2. Rex, a. 2011. Podstawy fizyki. osoba. 33 - 36
3. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14^th. Wyd. Tom 1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Podstawy fizyki. 9^na Wyd. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fizyka 10. Edukacja Pearsona. 133 - 149.