Ortonormalne właściwości podstawy, przykłady i ćwiczenia

A Baza ortonormalna Powstaje z wektorów prostopadłych ze sobą i których moduł jest również wart 1 (wektory jednostkowe). Pamiętaj, że baza B w przestrzeni wektorowej V, Jest zdefiniowany jako zestaw wektorów niezależnych liniowych, które mogą generować tę przestrzeń.

Z kolei przestrzeń wektorowa jest abstrakcyjną istotą matematyczną między których elementami są wektory, ogólnie związane z wielkościami fizycznymi, takimi jak prędkość, wytrzymałość i przemieszczenie, lub także z matrycami, wielomianami i funkcjami.

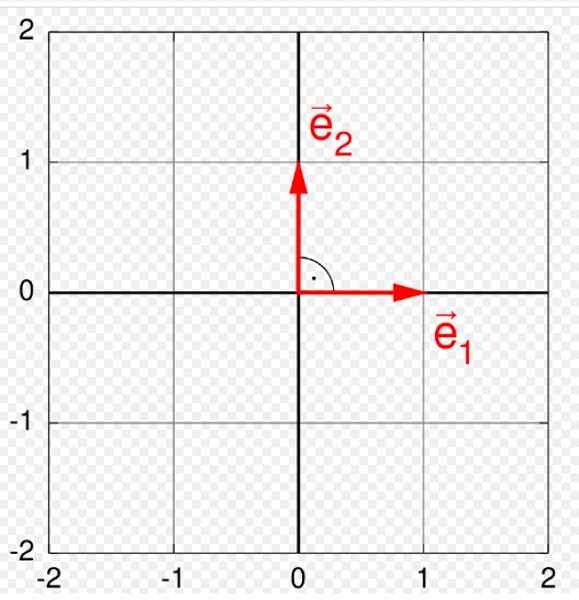
Rysunek 1. Podstawa ortonormalna w płaszczyźnie. Źródło: Wikimedia Commons. Quartl [CC BY-SA (https: // creativeCommons.Org/licencje/by-sa/3.0)].

Wektory mają trzy charakterystyczne elementy: wielkość lub moduł, kierunek i znaczenie. Baza ortonormalna jest szczególnie przydatna do reprezentowania i działania z nimi, ponieważ każdy wektor należący do określonej przestrzeni wektorowej V, Można go zapisać jako liniową kombinację wektorów, które tworzą podstawę ortonormalną.

W ten sposób operacje między wektorami, takimi jak suma, odejmowanie i różne typy produktów zdefiniowane we wspomnianej przestrzeni, są analizowane.

Wśród najczęściej używanych podstaw fizyki jest podstawa utworzona przez wektory jednostkowe Siema, J I k reprezentujące trzy charakterystyczne kierunki trzech wymiarów przestrzeni: wysokie, szerokie i głębokość. Wektory te są również znane pod nazwą Jednolite wektory kanoniczne.

Gdyby zamiast tego wektory będą działać w samolocie, wystarczyłoby to dwóm z tych trzech komponentów, a tylko jeden.

[TOC]

Podstawy właściwości

1- baza B Jest to najmniejszy możliwy zestaw wektorów, które generują przestrzeń wektorową V.

2- Elementy B Są liniowo niezależne.

3- Każda baza B przestrzeni wektorowej V, pozwala wyrażać wszystkie wektory V jako jego liniowa kombinacja, a ta forma jest unikalna dla każdego wektora. Dlatego B Jest również znany jako System generatora.

4- Ta sama przestrzeń wektorowa V może mieć różne podstawy.

Może ci służyć: siła odśrodkowa: formuły, jak jest obliczane, przykłady, ćwiczenia

Przykłady baz

Poniżej kilku przykładów ortonormalnych zasad i zasad ogólnie:

Baza kanoniczna w ℜ ^N

Zwany także naturalną podstawą lub standardową podstawą ℜ ^N, Gdzie ℜ ^N To jest przestrzeń N-wymiarowy, Na przykład trzy -wymiar przestrzeni wynosi ℜ ³. Do wartości N Nazywa się wymiar przestrzeni wektorowej i oznacza jako Dim (v).

Wszystkie wektory należące do ℜ ^N Są reprezentowane przez N-usa Zamówiono. Dla przestrzeni ℜ^N, Baza kanoniczna to:

I₁ =; I₂ =; I_N =

W tym przykładzie wykorzystaliśmy notację z nawiasami lub „wspornikami” i odważnym dla wektorów jednostkowych I₁, I₂, I₃..

Baza kanoniczna w ℜ³

Wektory rodzinne Siema, J I k Przyznają tę samą reprezentację i wystarczą do trzech, aby reprezentować wektory w ℜ ³:

Siema =; J =;  k =

Oznacza to, że podstawę można wyrazić w następujący sposób:

B = ; ;

Aby sprawdzić, czy są one liniowo niezależne, wyznacznik utworzony z nimi wektorów nie jest zerowy, a także równy 1:

Musi być również możliwe napisanie dowolnego wektora, który należy do ℜ ³ Jako ich liniowa kombinacja. Na przykład siła, której prostokątne elementy to f_X = 4 N, F_I = -7 n i f_z= 0 n byłby napisany w formie wektora w następujący sposób:

F = N = 4Siema -7J + 0k N.

Dlatego Siema, J I k Ustaw system generatora ℜ ³.

Inne bazy ortonormalne w ℜ³

Standardowa podstawa opisana w poprzednim rozdziale nie jest jedyną bazą ortonormalną w ℜ³. Tutaj mamy na przykład podstawy:

B₁ = ;; ;

B₂ = ;; ;

Można wykazać, że podstawy te są ortonormalne, ponieważ pamiętamy to warunki, które należy spełnić:

Może ci służyć: pofalowana optyka

-Wektory, które tworzą podstawę, muszą być dla siebie ortogonalne.

-Każdy z nich musi być jednolity.

Możemy to zweryfikować, wiedząc, że utworzone przez nich wyznacznik musi być nie -zerowy i równy 1.

Baza b₁ Jest to dokładnie takie cylindryczne współrzędne ρ, φ i z, inny sposób wyrażania wektorów w przestrzeni.

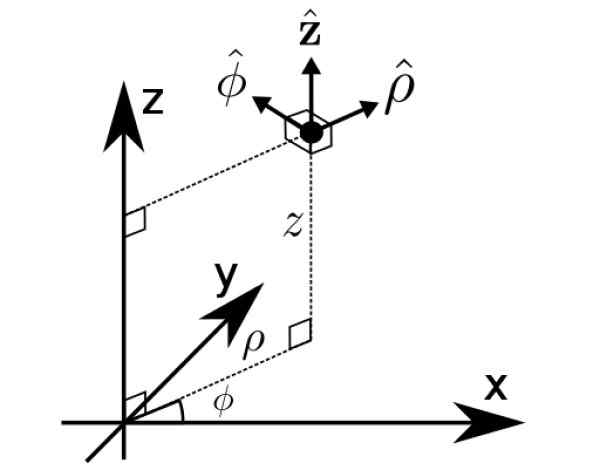Rysunek 2. Współrzędne cylindryczne. Źródło: Wikimedia Commons. Math Buff [CC BY-S (https: // creativeCommons.Org/licencje/nabrzeże/4.0)].

Rozwiązane ćwiczenia

- Ćwiczenie 1

Pokaż, że podstawa b = ; ; jest ortonormal.

Rozwiązanie

Aby pokazać, że wektory są prostopadłe do siebie, użyjemy produktu skalarnego, zwanego także punktem wewnętrznym lub produktu dwóch wektorów.

Niech dowolne dwa wektory Lub I v, Twój produkt skalarny jest zdefiniowany przez:

Lub • • v = Lub.v. cosθ

Aby odróżnić wektory od ich modułów. θ jest kątem pomiędzy Lub I v, Dlatego jeśli są prostopadłe, oznacza to, że θ = 90º i produkt skalarny jest nieważny.

Alternatywnie, jeśli wektory są podawane w kategoriach ich komponentów: Lub = X, Lub_I,Lub_z > i v = X, v_I,v_z >, produkt skalarny obu, który jest do pracy, jest obliczany w ten sposób:

Lub • • v = Lub_X .v_X + Lub_I .v_I + Lub_z .v_z

W ten sposób produkty skalarne między każdą parą wektorów są odpowiednio:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Dla drugiego warunku obliczany jest moduł każdego wektora, który jest uzyskiwany przez:

│u │ = √ (u_X² + Lub_I² + Lub_z²)

Zatem moduły każdego wektora to:

│ = √ [(3/5)² + (4/5)²  + 0²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Może ci służyć: Druga równowaga Warunek: wyjaśnienie, przykłady, ćwiczenia

│ = √ [0² + 0²  + 1²)] = 1

Dlatego trzy to wektory jednostkowe. Wreszcie, wyznacznik, który tworzą, nie jest zerowy i równy 1:

- Ćwiczenie 2

Napisz współrzędne wektorowe W = Pod względem poprzedniej bazy.

Rozwiązanie

Aby to zrobić, stosuje się następujące twierdzenie:

Niech B = v₁, v₂, v₃,.. v_N Baza ortonormalna w przestrzeni V z produktem krajowym, wektor W Jest reprezentowany przez B w następujący sposób:

W = <W• •v₁> v₁ + <W• •v₂> v₂ +<W• •v₃> v₃ +.. <W• •v_N> v_N

Oznacza to, że możemy napisać wektor u podstawy B, przez współczynniki <W• •v₁>, <W• •v₂>, ..  <W• •v_N>, dla których musisz obliczyć wskazane skalary:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

Z uzyskanymi produktami skalarnymi zbudowana jest matryca, nazywana Matryca współrzędna w.

Dlatego współrzędne wektora W W bazie B są wyrażane przez:

[[[W]_B= [[[(18/5); (1/5); 1]

Matryca współrzędnych nie jest wektorem, ponieważ wektor nie jest taki sam, jak jego współrzędne. Są to tylko zestaw liczb, które służą do wyrażania wektora u danej podstawy, a nie wektor jako taki. Zależą również od wybranej bazy.

Wreszcie, po twierdzeniu, wektor W zostałby wyrażony w następujący sposób:

W = (18/5) v₁ + (1/5) v₂ + v₃

Z: v₁ =; v₂ =; v₃ =, To znaczy wektory podstawowe B.

Bibliografia

1. Larson, r. Podstawy algebry liniowej. 6th. Wydanie. Cengage Learning.
2. Larson, r. 2006. Obliczenie. 7th. Wydanie. Głośność 2. McGraw Hill.
3. Salas, J. algebra liniowa. Temat 10. Bazy ortonormalne. Odzyskane z: OCW.UC3M.Jest.
4. Uniwersytet Sevilla. Współrzędne cylindryczne. Baza wektorowa. Odzyskany z: Laplace.nas.Jest.
5. Wikipedia. Baza ortonormalna. Odzyskane z: jest.Wikipedia.org.