Formuły i równania antideriwalne, przykłady, ćwiczenia

A Antiderivative F (x) funkcji F(x) jest również nazywane prymitywnymi lub po prostu nieokreślonymi całką wspomnianej funkcji, jeśli w danym przedziale Siema, To prawda, że F '(x) = f (x)

Na przykład weźmy następującą funkcję:

f (x) = 4x³

Antiderivative z tej funkcji to f (x) = x⁴, ponieważ uzyskując F (x) przez zasadę wyprowadzania dla mocy:

Jest uzyskiwany dokładnie f (x) = 4x³.

Jest to jednak tylko jeden z wielu antyiderivative F (x), ponieważ ta inna funkcja: g (x) = x⁴ + 2 Jest to również, ponieważ wyprowadzając g (x) w odniesieniu do x, jest to samo uzyskiwane z powrotem f (x).

Sprawdźmy to:

Pamiętaj, że ten pochodzący ze stałej to 0. Dlatego do terminu x⁴ Możesz dodać dowolną stałą, a jej pochodna będzie nadal 4x³.

Stwierdzono, że każda funkcja formularza ogólnego F (x) = x⁴ + C, gdzie C jest prawdziwą stałą, służy jako antykiwatywna F (x).

Poprzedni przykład ilustracyjny można wyrazić w następujący sposób:

df (x) = 4x³ Dx

Niezdefiniowana antideriwacyjna lub całka jest wyrażana z symbolem ∫, dlatego:

F (x) = ∫4x³ dx = x⁴ + C

Gdzie funkcja f (x) = 4x³  Nazywa się integracja, a C jest Stała integracji.

[TOC]

Przykłady antiderivative

Rysunek 1. Anti -Hotley jest niczym więcej niż nieokreśloną całką. Źródło: Pixabay.

Znalezienie antiderizacji funkcji jest proste w niektórych przypadkach, w których pochodne są dobrze znane. Na przykład, bądź funkcją f (x) = Sen x, ujednolicony dla niej jest inna funkcja f (x), tak że po uzyskaniu jej uzyskiwania jest f (x).

Ta funkcja może być:

F (x) = - cos x

Sprawdźmy, że to prawda:

F '(x) = (- cos x)' =- (-sen x) = sin x

Dlatego możemy napisać:

∫Sen x dx = -cos x + c

Oprócz znajomości pochodnych, istnieją podstawowe i proste zasady integracji, aby znaleźć nieokreślone antyekrologiczne lub integralne.

Może ci służyć: kolejne pochodne

Bądź prawdziwą stałą, zatem:

1.- ∫kdx = k ∫dx = kx + c

2.- ∫kf (x) dx = k ∫f (x) dx

Jeśli funkcję H (x) można wyrazić jako sumę lub odejmowanie dwóch funkcji, wówczas jej nieokreślona całka jest:

3.- ∫h (x) dx = ∫ [f (x) ± g (x)] dx = ∫f (x) dx ± ∫g (x) dx

To jest właściwość liniowości.

Reguła mocy W przypadku całek można go ustalić w ten sposób:

Ta zasada ma oczywiste ograniczenie: od mianownika N +1 Nie można tego zrobić 0, a zatem n ≠ -1.

W przypadku n = -1 stosowana jest następująca reguła:

5.- ∫X ^-1 Dx = ln x +c

Łatwo jest wykazać, że pochodna Ln x to jest dokładnie X ^-1.

Równania różniczkowe

Równanie różniczkowe to takie, w którym nieznana jest pochodna.

Teraz, z poprzedniej analizy, łatwo jest zdać sobie sprawę, że odwrotną działaniem pochodnej jest nieokreślona antyekrologiczna lub integralna.

Niech f (x) = y '(x), to znaczy pochodzący z określonej funkcji. Możemy użyć następującej notacji, aby wskazać tę pochodną:

Natychmiast następuje:

dy = f (x) dx

Nieznanym z równania różniczkowego jest funkcja y (x), ta, której pochodną jest f (x). Aby to wyczyścić, poprzednie wyrażenie jest zintegrowane po obu stronach, co jest równoważne z zastosowaniem antiderityzacji:

∫DY = ∫f (x) dx

Lewa całka jest rozwiązywana na podstawie reguły integracji 1, z k = 1, a zatem poszukiwany -awaite jest wyczyszczony:

i (x) = ∫f (x) dx = f (x) + c

A ponieważ C jest prawdziwą stałą, aby wiedzieć, co jest odpowiednie w każdym przypadku, instrukcja musi zawierać wystarczające dodatkowe informacje, aby obliczyć wartość C. To się nazywa Stan początkowy.

W następnej sekcji zobaczymy przykłady zastosowania tego wszystkiego.

Może ci służyć: punktualne oszacowanie

Ćwiczenia zhortowane

- Ćwiczenie 1

Zastosuj reguły integracji, aby uzyskać następujące nieokreślone antyeksywacje lub całki podanych funkcji, upraszczając wyniki w jak największym stopniu. Wygodne jest zweryfikowanie wyniku przez wyprowadzenie.

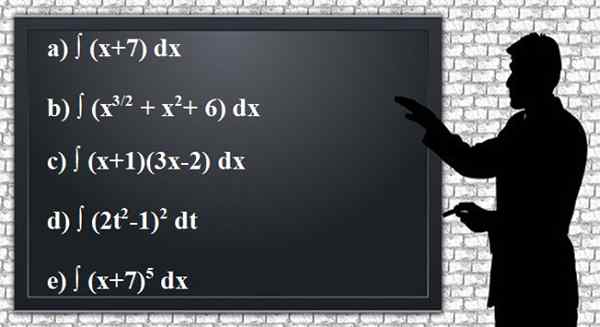Rysunek 2. Zdefiniowane ćwiczenia przednio lub integralne. Źródło: Pixabay.

Rozwiązanie

Najpierw stosujemy zasadę 3, ponieważ integracja jest sumą dwóch terminów:

∫ (x +7) dx = ∫ xdx +∫7dx

Dla pierwszej całki stosuje się zasadę mocy:

∫ xdx = (x² /2)+C₁

W drugiej regule integralnej 1 obowiązuje, wynosząc K = 7:

∫7dx = 7∫dx = 7x + c₂

A teraz wyniki są dodawane. Dwa stałe są pogrupowane w jedną, ogólnie zwaną C:

∫ (x+7) dx = (x² /2) + 7x + c

Rozwiązanie b

Przez liniowość ta integralna rozkłada się na trzy prostsze całki, do których zastosowano zasadę mocy:

∫ (x^3/2 + X² + 6) dx = ∫x^3/2 DX + ∫X² dx +∫6 dx =

= (2/5) x^5/2 + (1/3) x³ + 6x + c

Zauważ, że dla każdej całki pojawia się stała integracji, ale spotykają się w jednym połączeniu C.

Rozwiązanie c

W takim przypadku wygodne jest zastosowanie właściwości dystrybucyjnej mnożenia w celu opracowania integracji. Następnie używasz zasady uprawnień, aby znaleźć każdą całkę osobno, jak w poprzednim roku.

∫ (x+1) (3x-2) dx = ∫ (3x²-2x+3x-2) dx = ∫ (3x² + X - 2) dx

Uważny czytelnik zaobserwuje, że dwa centralne terminy są podobne, dlatego są one zmniejszone przed zintegrowaniem:

∫ (x+1) (3x-2) dx = ∫3x² dx + ∫ x dx + ∫- 2 dx = x³ + (1/2) x² - 2x + c

Rozwiązanie e

Sposobem na rozwiązanie całki byłoby rozwój władzy, jak to miało miejsce w przykładzie D. Jednak ponieważ wykładnik jest wyższy, konieczne byłoby dokonanie zmiennej zmiany, aby nie musiał dokonać tak długiego rozwoju.

Może ci służyć: ciągła losowa zmienna

Zmiana zmienna jest następująca:

U = x + 7

Po obu stronach to wyrażenie:

du = dx

Integral jest przekształcany w prostszą z nową zmienną, która jest rozwiązywana z zasadą mocy:

∫ (x+7)⁵ Dx = ∫ u⁵ du = (1/6) u⁶ + C

Wreszcie zmiana jest zwracana, aby powrócić do oryginalnej zmiennej:

∫ (x+7)⁵ Dx = (1/6) (x+7)⁶ + C

- Ćwiczenie 2

Cząstka jest początkowo spoczynkowa i porusza się wzdłuż osi x. Jego przyspieszenie dla t> 0 jest podane przez funkcję a (t) = cos t. Wiadomo, że przy t = 0 pozycja to x = 3, wszystkie w jednostkach systemu międzynarodowego. Poproszono o znalezienie prędkości v (t) i położenia x (t) cząstki.

Rozwiązanie

Ponieważ przyspieszenie jest pierwszym pochodzącym z prędkości w odniesieniu do czasu, masz następujące równanie różniczkowe:

a (t) = v '(t) = cos t

Wynika, że:

v (t) = ∫ cos t dt = sin t + c₁

Z drugiej strony wiemy, że prędkość jest z kolei pochodną pozycji, dlatego ponownie integrujemy się:

x (t) = ∫ v (t) dt = ∫ (sin t + c₁) dt = ∫Sen t dt + ∫c₁ dt = - cos t + c₁ T + c₂

Stałe integracyjne są określone na podstawie informacji podanych w oświadczeniu. Po pierwsze, mówi, że cząstka była początkowo w spoczynku, dlatego v (0) = 0:

V (0) = sin 0 + c₁ = 0

C₁ = 0

Wtedy musisz x (0) = 3:

x (0) = - cos 0 + c₁ 0 + c₂ = - 1 + C₂ = 3 → C₂ = 3+1 = 4

Funkcje prędkości i pozycji są zdecydowanie takie:

v (t) = sen t

x (t) = - cos t + 4

Bibliografia

1. Engler, a. 2019. Rachunek integralny. National University of the Coast.
2. Larson, r. 2010. Obliczanie zmiennej. 9na. Wydanie. McGraw Hill.
3. Darmowe teksty matematyki. Antiderivative. Odzyskane z: matematyki.Liibretexts.org.
4. Wikipedia. Antiderivative. Źródło: w:.Wikipedia.org.
5. Wikipedia. Integracja nieokreślona. Odzyskane z: jest.Wikipedia.org.