X kwadrat

Wyjaśniamy, co to jest X kwadrat, jego właściwości, przykłady i ćwiczenia zostały rozwiązane

Obszar kwadratu „x” jest x kwadratowy. Źródło: f. Zapata.

Działanie algebraiczne ”X kwadrat„Jest to przeprowadzane przez mnożenie ilości„ x ”dwukrotnie. Jest częścią operacji potencjałowych, a w symbolach matematycznych wyraża się w ten sposób:

x ∙ x = x²

Jest to szczególny przypadek wzmocnienia, w którym „x” reprezentuje baza A „2” jest wykładnik potęgowy. Jeśli w operacji pojawia się termin x², Odczytuje dokładnie jako „X kwadratowy” lub „x kwadrat podwyższony”.

Oczywiście możliwe są inne wykładniki, na przykład, jeśli wykładnik to 3, wówczas moc jest zapisywana jako:

x ∙ x ∙ x = x³

I przeczytaj jako „X do trzech”, „X podniesiony do kostki” lub po prostu „X do kostki”.

Ogólnie rzecz biorąc, wykładnik, do którego podstawa jest wysoka, może być dowolna liczba, zwana „n”, aw takim przypadku zapisana jest odpowiednia moc:

X^N = x ∙ x ∙ x ∙… ∙ x

Tutaj punkty zawiesinowe wskazują, że „x” musi zostać pomnożone sam w sobie „n”, to znaczy tyle razy, co wskaże wykładnik.

Niektóre proste przykłady „X kwadratowych” z liczbami są następujące:

3² = 3 ∙ 3 = 9

(-4)² = (−4) ∙ (−4) = 16

Później opisano różne aplikacje, dla których jest to konieczne.

Właściwości potencjałów

Ogólnie rzecz biorąc, iloczyn dowolnej kwoty, n razy, nazywa się on potencjał. Obliczanie X kwadratowych jest tylko szczególnym przypadkiem potencjału, pojawiają się dwa inne przypadki, gdy chcesz podnieść kwotę do wykładnika 1, w rezultacie otrzymując tę ​​samą kwotę:

Może ci służyć: prawa wykładników

Ponieważ te operacje są częste, aby pracować z bazami i wykładnikami, nazywane są pewne proste reguły operacyjne Prawa wykładników, które są wymienione poniżej:

Prawa wykładników

W dalszej części „X” jest podstawą, a „n” i „m” są wykładnikami.

1.- Produkt o równych mocach podstawowych

Poprzez pomnożenie dwóch (lub więcej) mocy o równej podstawie uzyskuje się podstawę podwyższoną do suma wykładników:

X^N∙ x^M = x^n+m

W przypadku X wysoki zasada ta jest stosowana w następujący sposób, zastępując N i M dla 1:

X¹∙ x¹ = x¹⁺¹ = x²

2.- Podział mocy równej bazy

Dzieląc moce tej samej podstawy, uzyskuje się podstawę, podniesiony do odejmowania między odpowiednimi wykładnikami licznika a mianownikiem:

X^N ÷ x^M = x^N-M

Ponieważ podział na 0 nie jest zdefiniowany, należy go spełnić, pod warunkiem, że x ≠ 0.

3.- Moc mocy

Wynik mocy mocy jest równy podstawie podwyższonej do produktu wykładników:

(X^M)^N = x^M∙N

Można go uzyskać ponownie x kwadrat, podczas wykonywania m = 1 i n = 2:

(X¹)² = x^1∙2 = x²

4.- Wykładnik ujemny

W przypadku wykładników ujemnych operacja, którą należy wykonać, wynosi:

Ilekroć x ≠ 0. Zauważ, że w tym przypadku moc staje się ułamkiem z licznikiem równym 1.

5.- Wykładnik ułamkowy

Wykładniki ułamkowe można zapisać jako n -tym korzenie podstawy:

Pod warunkiem, że n różni się od 0. Wartość ta staje się wskaźnikiem głównym, podczas gdy M staje się wykładnikiem ilości pod korzeniem, który w tym przypadku wynosi x.

Może ci służyć: jakie są wytyczne? (Geometria)

Produkty i iloraz różnych baz

Kiedy musisz ulepszyć produkty i iloraz różnych podstaw „X” i „Y”, zasady te są przestrzegane:

1.- Moc produktu

Aby wykonać tę moc, każda kwota jest podniesiona do wykładnika N i ustalany jest wynikowy produkt:

(x ∙ y)^N = x^N ⋅ i^N

2.- Stosunek ilorazu

Ponownie każda kwota musi zostać podniesiona do wykładnika n osobno i ustalić iloraz, który wynika, zgodnie z zasadą, że ilość „y” różni się od 0, w przypadku pozytywnego „n”:

(x ÷ y)^N = x^N ÷ y^N

Kiedy „n” jest negatywne, należy zachować ostrożność z powodu właściwości 4 poprzedniej sekcji, licznik staje się mianownikiem. W takim przypadku obie kwoty muszą być różne od 0, ponieważ należy unikać podziału o 0.

Przykłady

Przykład 1: kwadraty liczb naturalnych

Kwadraty pierwszych dziesięciu liczb naturalnych to:

• 1²= 1 × 1 = 1
• 2²= 2 × 2 = 4
• 3²= 3 × 3 = 9
• 4²= 4 × 4 = 16
• 5²= 5 × 5 = 25
• 6²= 6 × 6 = 36
• 7²= 7 × 7 = 49
• 8²= 8 × 8 = 64
• 9²= 9 × 9 = 81
• 10²= 10 × 10 = 100

Przykład 2: kwadrat liczb ujemnych

Kwadrat liczby ujemnej jest zawsze dodatni, ponieważ dwie ilości równych znaków są mnożone, dlatego:

(-x) · (-x) = x ∙ x = x²

Na przykład:

(-2) · (-2) = (-2)² = 4

Przykład 3: kwadrat suma i różnicy

Często konieczne jest obliczenie kwadratu sumy dwóch wielkości lub jego różnicy, operacje uwzględnione w kategorii znaczących produktów.

Operacja jest rozwiązywana z podanymi wskazaniami i pomocy nieruchomości dystrybucyjnej:

Kwadrat suma

Niech dwie kwoty „x” i „y” i chcesz znaleźć kwadrat jego sumę (x + y)²:

Może ci służyć: hierarchia operacji

(x + y)² = (x + y) ∙ (x + y) = x ∙ x + x ∙ y + y ∙ x + y ∙ y = x² + 2x ∙ y + i²

To wyrażenie brzmi: „Placu pierwszego, a także podwójny produkt pierwszego dla drugiego plus kwadrat drugiego”.

Kwadrat różnicy

Jest to rozwiązane analogicznie, ale biorąc pod uwagę znak ujemny:

(x - y)² = (x - y) ∙ (x - y) = x ∙ x - x ∙ y + y ∙ x - y ∙ y = x² - 2x ∙ i + i²

Przykład 4: Obszar kwadratu

Kwadrat jest wielokątem z 4, który ma tę samą miarę. Niech ℓ będzie pomiarem bocznym, a następnie obszar A rysunku jest podany przez:

A = ℓ²

Przykład 5: Twierdzenie Pitagoras

Twierdzenie to dotyczy trójkątów prostokątnych, na których dwie jego strony tworzą kąt prosty. Te strony są znane jako „kategorie”, a pozostałą stroną jest „hipotencja”.

Twierdzenie określa, że ​​kwadrat hipotenu jest równy sumie kwadratów kategorii. Nazywając „A” i „B” do kategorii i „C” do hipotenu, twierdzenie jest napisane jako:

C² = a² + B²

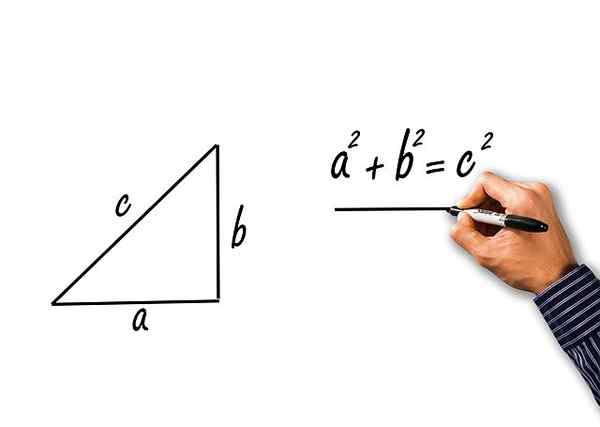Twierdzenie Pitagorasa dla prostokąta trójkąta kotów A i B oraz hipotenusa C

Rozwiązane ćwiczenia

Ćwiczenie 1

Oblicz kwadrat hipotenu, którego nogi mierzą 3 i 5 jednostek.

Rozwiązanie

Zgodnie z twierdzeniem Pitagorasa kwadrat przeciwprostokątności to:

C² = a² + B²

Zastępowanie wartości:

C² = 3² + 5²= (3 × 3) + (5 × 5) = 9 + 25 = 34

Ćwiczenie 2

Określ obszar bocznego kwadratu ℓ = 6 cm

Rozwiązanie

A = ℓ² = (6 cm)² = 36 cm²