Definicja prędkości kątowej, wzór, obliczenia i ćwiczenia

prędkość kątowa Jest to miara prędkości obrotu i jest definiowany jako kąt, który obraca wektor położenia obiektu, który obraca się, na jednostkę czasu. Jest to wielkość, która bardzo dobrze opisuje ruch wielu obiektów, które nieustannie obracają się wszędzie: CD, koła samochodowe, maszyny, Ziemia i wiele innych.

Schemat „London Eye” można zobaczyć na poniższej liczbie. Reprezentuje ruch pasażera reprezentowanego przez punkt P, który podąża za trajektorią kołową, zwaną C:

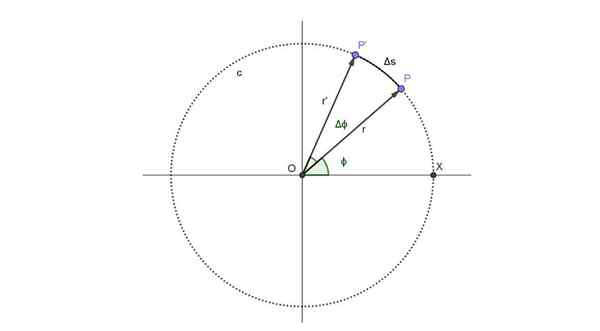Schematyczne przedstawienie okrągłej trajektorii, która podąża za pasażerem „Eye London Eye”. Źródło: Self Made.

Pasażer zajmuje pozycję p w natychmiastowej t, a pozycja kątowa odpowiadająca temu momentowi wynosi ϕ.

Od momentu upływu okresu δt. W tym okresie nowa pozycja punktualnego pasażera wynosi P ', a pozycja kątowa zwiększyła kąt 16.

[TOC]

Jak obliczana jest prędkość kątowa ?

W przypadku wielkości obrotowych litery greckie są szeroko stosowane, aby odróżnić je od wielkości liniowych. Tak więc początkowo zdefiniowana jest średnia prędkość kątowa ω_M Gdy kąt podróżował w danym okresie.

Wówczas iloraz cowy/δt będzie reprezentował średnią prędkość kątową ω_M Wśród chwil T i T+δT.

Jeśli chcesz obliczyć prędkość kątowa Właśnie w czasie t, wówczas iloraz cowy/δt będzie musiał zostać obliczony, gdy δT ➡0:

 Jednostka miary prędkości kątowej to Rad/s.

Zależność między prędkością liniową i kątową

Prędkość liniowa v, Jest to iloraz między przebywaną odległością a okresem używanym do podróży.

Na powyższym rysunku trasa łuku wynosi δs. Ale łuk ten jest proporcjonalny do przemieszczony kąt i promień, spełniając następującą zależność, która jest ważna, o ile 16 jest mierzone w radianach:

Może Ci służyć: Metoda równoległobramowa: przykłady, rozwiązane ćwiczenia

ΔS = r ・ 16

Jeśli podzielimy poprzednie wyrażenie między okresem δT i weźmiemy limit, gdy δT ➡0, otrzymamy:

v = r ・ ω

Jednolity ruch obrotu

Zdjęcie to słynne „London Eye”, obrotowe koło o mocy 135 m, które obraca się powoli, dzięki czemu ludzie mogą wsiąść do kabin u podstaw. Źródło: Pixabay.

Ruch obrotowy jest jednolity, jeśli w dowolnym momencie zaobserwowano, przemieszczony kąt jest taki sam w tym samym okresie czasu.

Jeśli obrót jest jednolity, wówczas prędkość kątowa w dowolnym momencie pokrywa się ze średnią prędkością kątową.

W jednolitym ruchu obrotu czasem, w którym całkowity zakręt nazywany jest okresem i oznacza T z T.

Ponadto, gdy kąt jest obrócony, jest on 2π (równoważny 360º). Dlatego w jednolitym obrocie prędkość kątowa ω jest związana z okresem t, za pomocą następującego wzoru:

Częstotliwość jest zdefiniowana F jednolitego rotacji, takiego jak iloraz między liczbą zwojów a czasem spędzonym na ich podróżowaniu. Jak 1 powrót podróżuje w czasie t (okres) ma następujący związek:

F = 1/t

Innymi słowy, w jednolitym obrocie prędkość kątowa jest powiązana z częstotliwością przez:

Ω = 2π ・ f

Rozwiązane ćwiczenia kątowe

Ćwiczenie 1

Kabiny wielkiego obracającego się koła znanego jako "Londyn„Poruszają się powoli. Prędkość kabin wynosi 26 cm/s, a koło ma średnicę 135 m.

Z tymi danymi oblicz:

Może ci służyć: słońce

i) prędkość kątowa koła

ii) Częstotliwość obrotu

iii) czas, który wymaga kabiny do odwrócenia.

Odpowiedzi:

Siema) Prędkość v w m/s wynosi: v = 26 cm/s = 0,26 m/s.

Radio ma połowę średnicy: r = (135 m) / 2 = 67,5 m

v = r ・ ω => ω = v/r = (0,26 m/s)/(67,5 m) = 0,00385 rad/s/s

Ii) Ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10^-4 Turns/s

F = 6,13 x 10^-4 Turn/s = 0,0368 Turn/min = 2,21 obrotu/godzinę.

Iii) T = 1 / f = 1/21 skrętu / godzinę = 0,45311 Czas = 27 min 11 sekund

Ćwiczenie 2

Samochód zabawki porusza. Po 0 s jego pozycja kątowa wynosi 0 rad, ale po pewnym czasie jego pozycji kątowej jest podana przez:

φ (t) = 2 ・ t 

Określić:

i) prędkość kątowa 

ii) prędkość liniowa w dowolnym momencie.

Odpowiedzi:

Siema) Prędkość kątowa jest pochodną pozycji kątowej: ω = φ '(t) = 2.

Innymi słowy.

Ii) Prędkość liniowa samochodu wynosi: v = r ・ ω = 2 m ・ 2 rad/s = 4 m/s = 14,4 km/h

Ćwiczenie 3

Ten sam samochód z poprzedniego ćwiczenia zaczyna się zatrzymać. Jego pozycja kątowa jako funkcji czasu jest podana przez następujące wyrażenie:

φ (t) = 2 ・ t - 0,5 ・ t² 

Określić:

i) prędkość kątowa w dowolnym momencie

ii) prędkość liniowa w dowolnym momencie

iii) czas, który poświęcisz, aby zatrzymać się od momentu zwalniania

iv) Kąt podróżował 

v) w przejechanej odległości

Odpowiedzi:

Siema) Prędkość kątowa jest pochodną pozycji kątowej: ω = φ '(t)

Ω (t) = φ '(t) = (2 ・ t - 0,5 ・ t²) '= 2 - t

Ii) Liniowa prędkość samochodu w dowolnym momencie jest podana przez:

v (t) = r ・ ω (t) = 2 ・ (2 - t) = 4 - 2 t

Może ci służyć: względna prędkość: koncepcja, przykłady, ćwiczenia

Iii) Czas, który przyjmuje moment, w którym zaczyna spowolnić.

v (t) = 4 - 2 t = 0 => t = 2

To znaczy, że po rozpoczęciu zatrzymania się zatrzymuje 2 s.

Iv) W okresie 2s, od czasu, gdy zaczyna się zatrzymać, aż do podróży przez φ (2):

φ (2) = 2 ・ 2 - 0,5 ・ 2^2 = 4 - 2 = 2 rad = 2 x 180 / π = 114,6 stopni

V) W rozprzestrzenianiu się 2 s, ponieważ zaczyna się zatrzymać, dopóki nie zatrzyma odległości S przez:

S = r ・ φ = 2m ・ 2 rad = 4 m

Ćwiczenie 4

Koła samochodu mają średnicę 80 cm. Jeśli samochód porusza się z prędkością 100 km/h. Znajdź: i) prędkość kątowa obrotu koła, ii) częstotliwość obrotu kół, iii) liczba okrążeń, które koło podaje na 1 -godzinnej trasie.

Odpowiedzi:

Siema) Po pierwsze, obrócimy prędkość samochodu km/h m/s

V = 100 km / h = (100/3.6) m/s = 27,78 m/s

Prędkość kątowa obrotu kół jest podana przez:

Ω = v/r = (27,78 m/s)/(0,4 m) = 69,44 rad/s

Ii) Częstotliwość obrotu kół jest podana przez:

F = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 obrotu / s

Częstotliwość obrotu jest zwykle wyrażana w obrotach na minutę r.P.M.

F = 11,05 obrotu/s = 11,05 obrotu/(1/60) min = 663,15 r.P.M

Iii)  Liczba zakrętów, które koło podaje na 1 -godzinną trasę, jest obliczana, wiedząc, że 1 godzina = 60 min i że częstotliwość jest liczbą zakrętów n podzielonych przez czas, w którym podano te n.

F = n / t => n = f ・ t = 663,15 (skręty / min) x 60 min = 39788,7 tury.

Bibliografia

1. Giancoli, zm. Fizyka. Zasady z aplikacjami. 6. edycja. Prentice Hall. 106-108.
2. Resnick, r. (1999). Fizyczny. Tom 1. Trzecie wydanie po hiszpańsku. Meksyk. Continental Editorial Company S.DO. c.V. 67-69.
3. Serway, r., Jewett, J. (2008). Fizyka nauk i inżynierii. Tom 1. 7th. Wydanie. Meksyk. Redaktorzy edukacyjni Cengage. 84-85.
4. Geogebra.org