Wektory kolinealne

Wyjaśniamy, jakie są wektory Colineal, system wektorów Colineal i umieściliśmy kilka przykładów

Jakie są wektory Collineal?

Wektory kolinealne Są jednym z trzech rodzajów istniejących wektorów. Są to wektory, które są w tym samym kierunku lub linii działania. Oznacza to, że następujące: dwa lub więcej wektorów będzie Colineal, jeśli istnieje, że są one ułożone w liniach, które są do siebie równoległe.

Wektor jest zdefiniowany jako wielkość zastosowana do ciała i charakteryzuje się kierunkiem, sensem i skalą. Wektory można znaleźć w płaszczyźnie lub w przestrzeni i mogą być różnych typów: wektory kolineal, wektory współbieżne i wektory równoległe.

Kiedy istnieją wektory Collineal?

Wektory są kolineal, jeśli linia działania jednego jest dokładnie ta sama linia działania wszystkich innych wektorów, niezależnie od wielkości i kierunku każdego z wektorów.

Wektory są stosowane jako reprezentacje w różnych obszarach, takich jak matematyka, fizyka, algebra, a także w geometrii, w których wektory są kolineal tylko wtedy, gdy ich kierunek jest taki sam, niezależnie od tego, że ich znaczenie nie jest.

Przykłady wektorów kolinealnych

• Dwa lub więcej wektorów jest kolineal, jeśli związek między współrzędnymi jest taki sam.

Przykład 1

Masz wektory m = m_x; m_y i n = n_x; N_. Są to kolinearne, jeśli:

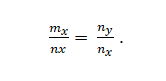
Przykład 2

Można ustalić, czy wektory j = 3,6,15 i p = 1,2,5 są wspólne poprzez związek ich współrzędnych, które musisz być proporcjonalny; to jest do powiedzenia: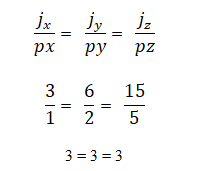

• Dwa lub więcej wektorów jest kolineal, jeśli mnożenie produktu lub wektora jest równe zero (0). Wynika to z faktu, że w układzie współrzędnych każdy wektor charakteryzuje się ich odpowiednimi współrzędnymi, a jeśli są one proporcjonalne do siebie, wektory będą kolinearne. Wyraża się to w następujący sposób:

Może ci służyć: równoważne zestawy: co to są, wyjaśnienie, przykłady

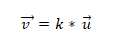
Przykład 1

Masz wektory a = (10, 5) i b = (6, 3). Aby ustalić, czy są one kolineal, stosuje się teorię określania, która określa równość produktów krzyżowych. W ten sposób musisz:

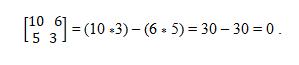
System wektorowy Colineal

Wektory Colineal są reprezentowane graficznie za pomocą kierunku i kierunku - mając na uwadze, że muszą one przejść przez punkt zastosowania - i moduł, który jest określoną skalą lub długością.

System wektora Colineal powstaje, gdy dwa lub więcej wektorów działa na obiekt lub ciało, które reprezentują siłę i działają w tym samym kierunku.

Na przykład, jeśli na ciele nałożone są dwie siły kolineal, powstały jeden z nich będzie zależeć tylko od poczucia, w którym działają. Istnieją trzy przypadki, które są:

Wektory kolinealowe z przeciwnymi zmysłami

Powstałe dwóch wektorów kolinalnych jest równe sumie z nich:

R = ∑ f = f₁ + F_2.

Przykład

Jeśli dwie siły F działają na wózku₁ = 40 N i F₂ = 20 N W przeciwnym kierunku (jak pokazano na obrazie), wynik jest:

R = ∑ f = (- 40 n) + 20n.

R = - 20 n.

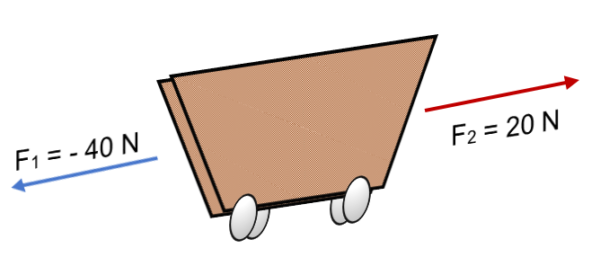Znak ujemny wyraża, że ​​ciało przesunie się w lewo, z siłą równoważną 20 N.

Wektory Colineal w tym samym sensie

Wielkość powstałej siły będzie równa sumie wektorów kolinalnych:

R = ∑ f = f₁ + F_2.

Przykład

Jeśli dwie siły F działają na wózku₁ = 35 N i F₂ = 55 N W tym samym kierunku (jak pokazano na obrazie), wynik jest:

R = ∑ f = 35 n + 55n.

R = 90 n.

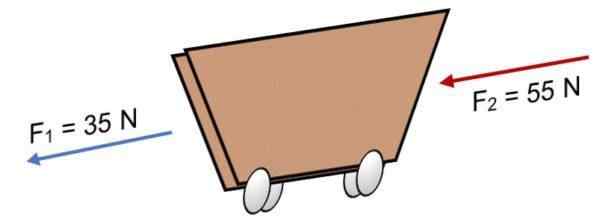
Wynik dodatni wskazuje, że wektory Collineal działają w lewo.

Może ci służyć: reguła t: Charakterystyka, tak że jest przykłady

Wektory kolinealowe o równych wielkościach i przeciwnych zmysłach

Wynik dwóch wektorów kolinialnych będzie równy sumę wektorów kolinearnych:

R = ∑ f = f₁ + F_2.

Ponieważ siły mają tę samą wielkość, ale w przeciwnym kierunku -to znaczy, że jeden będzie dodatni, a drugi ujemny -dodając dwie siły, wynik będzie równy zero.

Przykład

Jeśli dwie siły F działają na wózku₁ = -7 n i f₂ = 7 N, które mają tę samą wielkość, ale w przeciwnym kierunku (jak pokazano na obrazie), wynik jest:

R = ∑ f = (-7 n) + 7n.

R = 0.

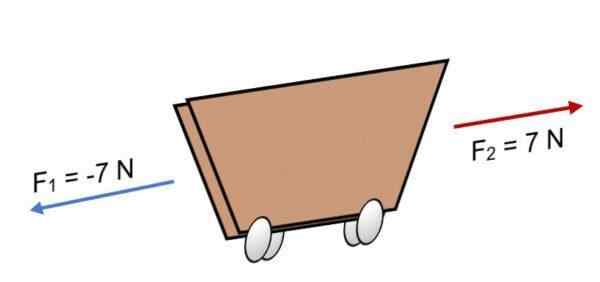
Ponieważ wynik jest równy 0, oznacza to, że wektory równoważą się ze sobą, a zatem ciało jest w równowadze lub odpoczynku (nie będzie się poruszać).

Różnica między wektorami kolinealnymi i współbieżnymi

Wektory Colineal charakteryzują się posiadaniem tego samego kierunku na tej samej linii lub dlatego, że są one równoległe do linii; To znaczy są wektorami reżyserów linii równoległych.

Ze swojej strony, współbieżne wektory są zdefiniowane, ponieważ znajdują się w różnych liniach działania, które są przechwycone w jednym punkcie.

Innymi słowy, mają ten sam punkt pochodzenia lub przybycia -niezależnie od swojego modułu, znaczenia lub kierunku -wyformując kąt między nimi.

Równoczesne systemy wektorowe są rozwiązywane metodami matematycznymi lub graficznymi, które są metodą sił równoległobramowych i metodą wielokąta sił. Za pomocą nich zostanie określona wartość uzyskanego wektora, co wskazuje kierunek, w którym porusza się ciało.

Zasadniczo główną różnicą między wektorami kolinearnymi i równoczesnymi jest linia działania, w którym działają: Collineals działają w tej samej linii, podczas gdy równoczesne w różnych.

Może ci służyć: system równań: metody rozwiązania, przykłady, ćwiczenia

Oznacza to, że wektory kolinearne działają w jednej płaszczyźnie „x” lub „y”; I współbieżne działanie w obu samolotach, zaczynając od tego samego punktu.

Wektory kolinealne nie są w pewnym momencie, jak to robią równoległe, ponieważ są one równoległe do siebie.

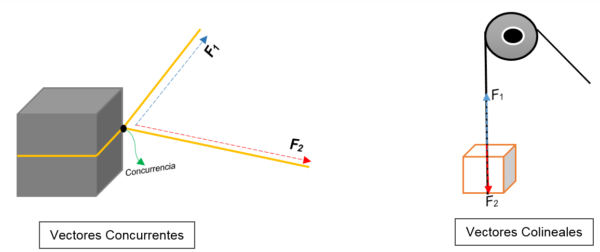
Na lewym obrazie możesz zobaczyć blok. Jest związany z liną, a węzeł dzieli ją na dwa; Po znalezieniu w kierunku różnych orientacji i różnych sił blok zmierzy się w ten sam kierunek.

W jednym punkcie (blok) reprezentuje dwa wektory, niezależnie od ich modułu, kierunku lub kierunku.

Z drugiej strony na prawym obrazie pojawia się koło pasowe, które podnosi pudełko. Lina reprezentuje linię działania; Po zatrzymaniu działają na nim dwie siły (wektory): siła napięcia (podczas wspinania się po bloku) i inna siła, która wywiera ciężar bloku. Oba mają ten sam kierunek, ale w przeciwnych zmysłach; W pewnym momencie nie zgadzają się.