Charakterystyka i właściwości wektora, elementy, typy, przykłady

wektory Są to istoty matematyczne, które mają pozytywną wielkość -zwykle towarzyszy jednostce miary, oprócz kierunku i znaczenia. Takie cechy są bardzo odpowiednie do opisania wielkości fizycznych, takich jak prędkość, siła, przyspieszenie i wiele innych.

Wektorów możliwe jest wykonywanie operacji, takich jak suma, odejmowanie i produkty. Podział nie jest zdefiniowany dla wektorów, a podobnie jak dla produktu, istnieją trzy klasy, które opiszemy później: produkt skalarny lub punktowy, wektor lub krzyżowy produkt i produkt skalarny dla wektora.

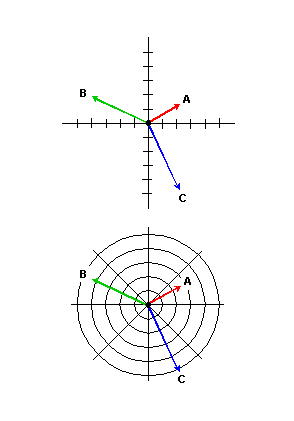
Rysunek 1. Elementy wektora. Źródło: Wikimedia Commons.

Aby całkowicie opisać wektor, konieczne jest wskazanie wszystkich jego właściwości. Wielkość lub moduł jest wartością liczbową, któremu towarzyszy jednostka, podczas gdy kierunek i znaczenie są ustalane za pomocą układu współrzędnych.

Spójrzmy na przykład: załóżmy, że samolot leci z jednego miasta do drugiego w tempie 850 km/h w kierunku. Tutaj mamy całkowicie określony wektor, ponieważ dostępna jest wielkość: 850 km/h, podczas gdy kierunek i znaczenie są NE.

Wektory są zwykle reprezentowane graficznie przez zorientowane segmenty linii, których długość jest proporcjonalna do wielkości.

Aby określić kierunek i znaczenie, wymagana jest linia odniesienia, która zwykle jest osą poziomą, chociaż Północ może być również traktowana jako odniesienie, taka jest taka prędkość płaszczyzny:

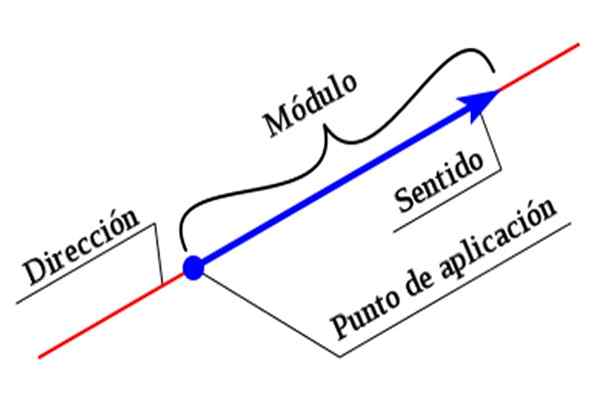
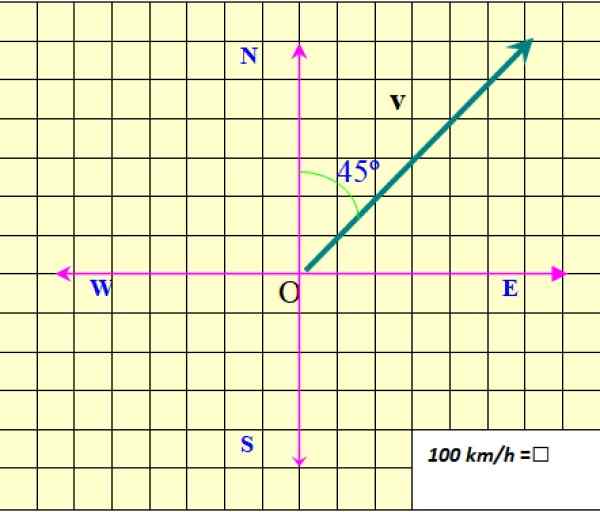Rysunek 2. Wektor prędkości. Źródło: f. Zapata.

Rysunek pokazuje wektor prędkości płaszczyzny, który jest oznaczony jako v W pogrubiony, Aby odróżnić go od wielkości skalarnej, która wymaga tylko wartości numerycznej i określonej jednostki.

[TOC]

Elementy wektora

Jak powiedzieliśmy, elementy wektorowe to:

-Wielkość lub moduł, czasami nazywany również wartością bezwzględną lub standardem wektora.

-Adres

-Sens

W przykładzie na rycinie 2 moduł v To 850 km/h. Moduł jest oznaczony jako V bez pogrubionego lub jako |v|, Gdzie słupki reprezentują wartość bezwzględną.

Adres v jest określony w odniesieniu do północy. W tym przypadku jest 45º na północ od wschodu (45º NE). Wreszcie wierzchołek strzałki informuje o kierunku v.

W tym przykładzie pochodzenie wektorowe zostało narysowane przez zbieżność z systemem pochodzenia lub współrzędnych, jest to znane jako Połączony wektor. Z drugiej strony, jeśli pochodzenie wektora nie pasuje do pochodzenia systemu odniesienia, mówi się, że jest to wolny wektor.

Należy zauważyć, że aby całkowicie określić wektor, te trzy elementy należy wskazać, w przeciwnym razie opis wektora byłby niekompletny.

Prostokątne składniki wektora

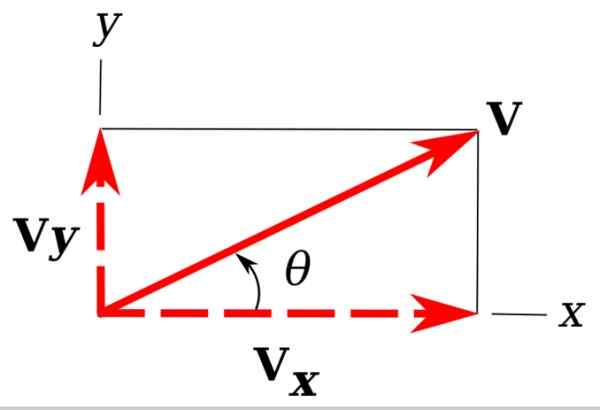Rysunek 3. Prostokątne składniki wektora w płaszczyźnie. Źródło: Wikimedia Commons. Untuer [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)]

Na obrazie mamy nasz przykład wektor v, to jest w samolocie Xy.

Łatwo zauważyć, że projekcje V na osiach współrzędnych x i y określają prawy trójkąt. Te projekcje są v_I I v_X i nazywane są prostokątnymi elementami v.

Sposób na oznaczenie v Poprzez prostokątne komponenty jest takie: v = X, v_I>. Te kwadratowe nawiasy są używane zamiast nawiasów, aby podkreślić fakt, że jest to wektor, a nie punkt, ponieważ w tym przypadku nawiasy będą używane nawiasy.

Może ci służyć: James Chadwick: Biografia, model atomowy, eksperymenty

Jeśli wektor znajduje się w przestrzeni trójwymiarowej, potrzebny jest jeszcze jeden składnik, tak::

v = X, v_I, v_z>

Znając prostokątne składniki, obliczana jest wielkość wektora, równoważna znalezieniu hipotenu prawego trójkąta, którego nogi są v_X I v_I,. Poprzez twierdzenie Pitagorasa następuje, że:

|v|² = (v_X)² +  (v_I)²

Polarna forma wektora

Gdy znana jest wielkość wektora |v| I kąt θ, że ta forma z osą odniesienia, zwykle osi pozioma, wektor jest równo określony. Następnie mówi się, że wektor jest wyrażany w postaci polarnej.

W tym przypadku łatwo obliczane są prostokątne komponenty:

v_X = |v|.cos θ

v_I = |v|.sin θ

Zgodnie z powyższym, prostokątne elementy wektora prędkości v samolotu byłoby:

v_X = 850 . cos 45º km/h = 601.04 km/h

v_I = 850 . Sen 45º km/h = 601.04 km/h

Chłopaki

Istnieją różne rodzaje wektorów. Istnieją wektory żyłowe, pozycja, przemieszczenie, siła, pole elektryczne, ilość ruchu i wiele innych. Jak już powiedzieliśmy, w fizyce jest wiele wielkości wektorów.

Jeśli chodzi o wektory, które mają pewne cechy, możemy wspomnieć o następujących typach wektorów:

-Zero: Są to wektory, których wielkość wynosi 0 i które są oznaczone jako 0. Pamiętaj, że odważna litera symbolizuje trzy podstawowe cechy wektora, podczas gdy normalna litera reprezentuje tylko moduł.

Na przykład o ciele w równowadze statycznej suma sił musi być wektorem zerowym.

-Darmowe i powiązane: Wolne wektory to te, których punktami pochodzenia i przybycia są dowolną parą punktów płaszczyzny lub przestrzeni, w przeciwieństwie do połączonych wektorów, których pochodzenie pokrywa się z punktem systemu referencyjnego używanego do ich opisania.

Para lub moment wyprodukowany przez kilka sił jest dobrym przykładem wolnego wektora, ponieważ moment obrotowy nie ma zastosowania do jakiegoś konkretnego punktu.

-Sprzęt: Są dwoma wolnymi wektorami, które mają identyczne cechy. Dlatego mają tę samą wielkość, kierunek i znaczenie.

-Coplanares lub coplanarios: wektory należące do tej samej płaszczyzny.

-Przeciwieństwa: wektory o równej wielkości i kierunku, ale przeciwne zmysły. Wektor przeciwny wektora v Jest to wektor -v A suma obu to wektor zerowy: v + (-v) = 0.

-Równoległy: wektory, których linie działania przechodzą przez ten sam punkt.

-Slajd: to wektory, których punkt aplikacji mogą przesunąć się wzdłuż określonej linii.

-Colineal: wektory znajdujące się na tej samej linii.

-Unitary: Te wektory, których moduł to 1.

Wektory jednostki ortogonalnej

Istnieje bardzo przydatny rodzaj wektora w fizyce zwanej wektorem jednostki ortogonalnej. Wektor jednostki ortogonalnej ma moduł równy 1, a jednostki mogą być dowolne, na przykład prędkość, pozycja, wytrzymałość lub inna.

Istnieje zestaw specjalnych wektorów, które pomagają łatwo reprezentować inne wektory i wykonywać z nimi operacje: są to wektory ortogonalne Siema, J I k, Unitary i prostopadle do siebie.

W dwóch wymiarach wektory te są skierowane w pozytywnym sensie obu osi X według osi I. A w trzech wymiarach dodaje się wektor jednostkowy w kierunku osi z pozytywny. Są reprezentowane w następujący sposób:

Może ci służyć: jaka jest struktura badań dokumentalnych?

Siema =

J =

k =

Wektor może być reprezentowany przez wektory jednostkowe Siema, J I k następująco:

v = v_X Siema + v_I J + v_z k

Na przykład wektor prędkości v Z poprzednich przykładów możesz napisać jako:

v = 601.04 Siema + 601.04 J km/h

Komponent w k Nie jest to konieczne, ponieważ ten wektor jest w płaszczyźnie.

Suma wektorów

Suma wektorów pojawia się bardzo często w różnych sytuacjach, na przykład, gdy chcesz znaleźć wynikową siłę na obiekcie, na który wpływa różne siły. Aby zacząć, przypuśćcie, że masz dwa bezpłatne wektory Lub I v w samolocie, jak następujące pokazują po lewej:

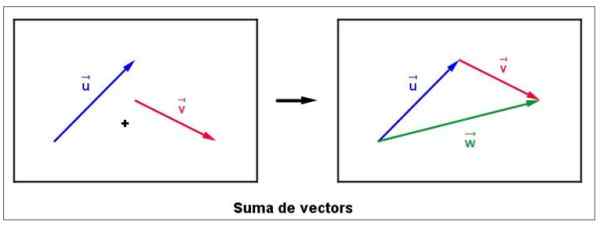Rysunek 4. Suma graficzna dwóch wektorów. Źródło: Wikimedia Commons. LLUC CABANACH [CC BY-SA 3.0 (https: // creativeCommons.Org/licencje/by-sa/3.0)].

Natychmiast przenosi się do wektora v, bez modyfikowania jego wielkości, kierunku lub znaczenia, tak aby powstało z końcem Lub.

Wektor sumowy jest nazywany W i jest narysowany, zaczynając od ukończenia v, Zgodnie z prawą figurą. Należy zauważyć, że wielkość wektora W Niekoniecznie jest to suma wielkości v I Lub.

Jeśli jest to starannie odzwierciedlone w tym względzie, jedyną okazją, gdy wielkość powstałego wektora jest suma wielkości dodanych, to wtedy, gdy obaj uzależnieni są w tym samym kierunku i mają to samo znaczenie.

I co się stanie, jeśli wektory nie są wolne? Bardzo łatwo je dodać. Sposobem jest dodanie komponentu komponentu lub metody analitycznej.

Jako przykład, rozważmy wektory poniższej liczby, pierwszą rzeczą jest wyrażanie ich z jednej z wcześniej wyjaśnionych formantów:

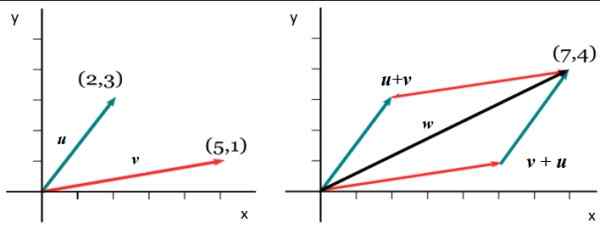Rysunek 5. Suma dwóch połączonych wektorów. Źródło: Wikimedia Commons.

v =

Lub =

Aby uzyskać komponent w X wektora dodaje W, Odpowiednie komponenty są dodawane X z v I Lub: W_X = 5+2 = 7. I zdobyć W_I Przestrzegana jest analogiczna procedura: w_I = 1+3. Dlatego:

Lub =

Właściwości suma wektorów

-Suma dwóch lub więcej wektorów powoduje inny wektor.

-Jest ono zgodne, kolejność dodatków nie zmienia sumy, aby:

Lub + v = v + Lub

-Neutralnym elementem sumy wektorów jest wektor zerowy: v + 0 = v

-Odejmowanie dwóch wektorów jest zdefiniowane jako suma przeciwnego: V - u = v + (-Lub)

Przykłady wektorów

Jak powiedzieliśmy, w fizyce istnieje wiele ilości wektorów. Wśród najbardziej znanych są:

-Pozycja

-Przemieszczenie

-Średnia prędkość i natychmiastowa prędkość

-Przyśpieszenie

-Siła

-Ilość ruchu

-Moment obrotowy lub moment siły

-Impuls

-pole elektryczne

-Pole magnetyczne

-Moment magnetyczny

Z drugiej strony nie są wektorami, ale wspinają się:

-Czas

-Masa

-Temperatura

-Tom

-Gęstość

-Praca mechaniczna

-Energia

-Ciepło

-Moc

-Napięcie

-Prąd elektryczny

Inne operacje między wektorami

Oprócz sumy i odejmowania wektorów istnieją trzy inne operacje między bardzo ważnymi wektorami, ponieważ powodują one nowe, bardzo ważne wielkości fizyczne:

-Produkt skalarny dla wektora.

-Produkt skalarny lub produkt punktowy między wektorami

-Oraz produkt krzyżowy lub wektorowy między dwoma wektorami.

Produkt skalarny dla wektora

Rozważ drugie prawo Newtona, które stwierdza, że ​​ta siła F i przyspieszenie Do Są proporcjonalne. Stała proporcjonalności jest masa M obiektu, zatem:

F = m.Do

Ciasto to skalar; Ze swojej strony siła i przyspieszenie to wektory. Ponieważ siła uzyskuje się przez pomnożenie masy przez przyspieszenie, jest wynikiem produktu skalarnego przez wektor.

Może ci służyć: przykłady ram teoretycznych

Ten rodzaj produktu zawsze powoduje wektor. Tutaj kolejny przykład: ilość ruchu. Być P Wektorowa ilość ruchu, v Wektor prędkości i jak zawsze, M to masa:

P = m.v

Produkt skalarny lub produkt punktowy między wektorami

Umieściliśmy prace mechaniczne na liście wielkości, które nie są wektorami. Jednak praca w fizyce jest wynikiem operacji między wektorami zwanymi produktem skalarnym, produktem wewnętrznym lub produktem punktowym.

Być wektorami v I Lub, Punkt lub produkt wspinaczkowy jest między nimi zdefiniowany:

v∙Lub = |v|. ∙ |Lub |.cos θ

Będąc θ kątem między nimi. Z pokazanego równania natychmiast wydedukowano, że wynikiem punktu produktu jest skalar, a także jeśli oba wektory są prostopadłe, ich produkt skalarny wynosi 0.

Powrót do pracy mechanicznej W, To jest produkt skalarny między wektorem wytrzymałościowym F i przemieszczenie wektora ℓ.

W = F∙ℓ                  

Gdy wektory są dostępne pod względem ich komponentów, produkt punktowy jest również bardzo prosty do obliczenia. Tak v = X, v_I, v_z > I Lub = X, Lub_I, Lub_z >, Produkt punktowy między nimi to:

v∙Lub = v_X Lub_X + v_I Lub_I + v_z Lub_z

Produkt punktowy między wektorami jest zatem do pracy, zatem:

v∙Lub = Lub∙v

Produkt krzyżowy lub produkt wektorowy między wektorami

Tak v a u są naszymi dwoma przykładowymi wektorami, produkt wektorowy jest zdefiniowany jako:

v X Lub = W

Natychmiast wynika z tego, że produkt krzyżowy powoduje wektor, którego moduł jest zdefiniowany jako:

|v X u | = | V | . | U |. sin θ

Gdzie θ Jest to kąt między wektorami.

Dlatego produkt krzyżowy nie jest przedmiotem pracy v X u ≠ u X v. W rzeczywistości v X U = - (u X V).

Jeśli dwa przykładowe wektory są wyrażone w kategoriach wektorów jednostkowych, ułatwia się obliczenie produktu wektorowego:

v = v_X Siema + v_I J + v_z k

Lub = u_X Siema + Lub_I J + Lub_z k

Produkty między wektorami jednostkowymi

Produkt krzyżowy między identycznymi wektorami jednostkowymi jest zerowy, ponieważ kąt między nimi wynosi 0º. Ale wśród różnych wektorów jednostkowych kąt między nimi wynosi 90º i Sin 90º = 1.

Poniższy schemat pomaga znaleźć te produkty. W kierunku strzałki ma to pozytywny sens i w przeciwnym kierunku:

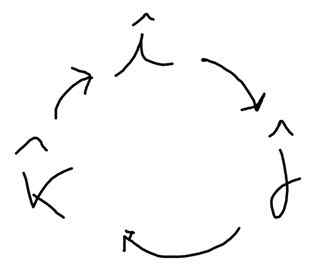
Siema X J = K, J X k = Siema; k X Siema = J; J X i = -k; k X J = -Siema; Siema X k = -J

Stosując nieruchomość dystrybucyjną, która pozostaje ważna dla produktów wśród wektorów oraz właściwości wektorów jednostkowych, masz:

v X Lub = (v_X Siema + v_I J + v_z k) X (u_X Siema + Lub_I J + Lub_z k) =  

= (v_ILub_z - v_zLub_I )Siema + (v_zLub_X - v_XLub_z )J + (v_XLub_I - v_ILub_X )k

Rozwiązane ćwiczenia

- Ćwiczenie 1

Biorąc pod uwagę wektory:

v = -5 Siema + 4J + 1 k

Lub = 2 Siema -3 J + 7k

Co powinno być wektor W tak suma v + Lub + W wyniki 6 Siema +8 J -10k?

Rozwiązanie

-5 Siema + 4J + 1 k

2 Siema -3 J + 7k

 W_X Siema + W_I J + W_z k  +

--

6Siema + 8 J -10 k

Dlatego należy spełnić, że:

-5 +2 + w_X = 6 → W_X = 9

4-3 + w_I = 8 → W_I = 7

1 + 7 + w_z = -10 → w_z = -18

Odpowiedź to: W = 9 Siema +7 J - 18k

- Ćwiczenie 2

Jaki jest kąt między wektorami v I Lub ćwiczenia 1?

Rozwiązanie

Użyjemy produktu skalarnego. Mamy:

cos θ = v∙Lub / |v|. ∙ |Lub|

v∙Lub= -10 -12+7 = -15

|v| = √ (-5)² +4² +1²= √42 = 6.48

|Lub| = √2² +(-3)² +7²= √62 = 7.87

Zastąpienie tych wartości:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → θ = 107.1st

Bibliografia

1. Figueroa, zm. (2005). Seria: Fizyka nauk i inżynierii. Tom 1. Kinematyka. Pod redakcją Douglas Figueroa (USB).
2. Giancoli, zm.  2006. Fizyka: zasady z aplikacjami. 6th. Ed Prentice Hall.
3. Rex, a. 2011. Podstawy fizyki. osoba.
4. Sears, Zemansky. 2016. Fizyka uniwersytecka z nowoczesną fizyką. 14. Wyd. Tom 1.
5. Serway, r., Jewett, J. 2008. Fizyka nauk i inżynierii. Tom 1. 7th. Wyd. Cengage Learning.