Całkowita wartość

Jaka jest wartość bezwzględna?

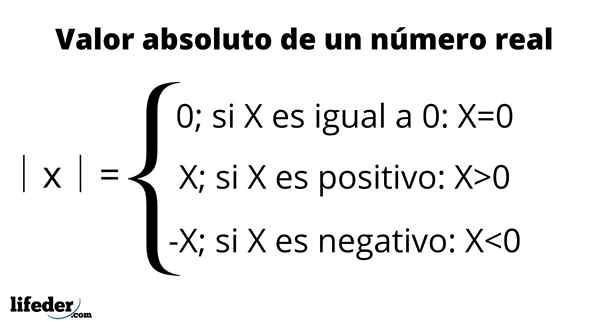
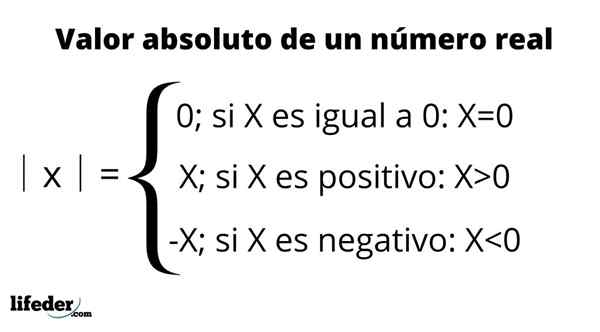
On całkowita wartość liczby rzeczywistej jest zdefiniowana jako odległość między tą liczbą a 0 linii rzeczywistej. Ponieważ jest odległość, jego wartość jest zawsze dodatnia lub zerowa i równa liczbie liczby.

Wartość bezwzględna jest reprezentowana przez umieszczenie liczby między dwoma pionowymi prętami, który jest czytany: "wartość bezwzględna”, Jak podsumowano w poniższej tabeli:

Na przykład wartość bezwzględna -3 jest zapisywana jako │ -3│ i jest równa 3. Oznacza to, że między -3 a 0 istnieją trzy jednostki, które reprezentują liczby na linii rzeczywistej. Z drugiej strony wartość bezwzględna +3 lub po prostu 3, jest również równa 3, ponieważ pomiar jej odległości do 0 to także trzy jednostki.

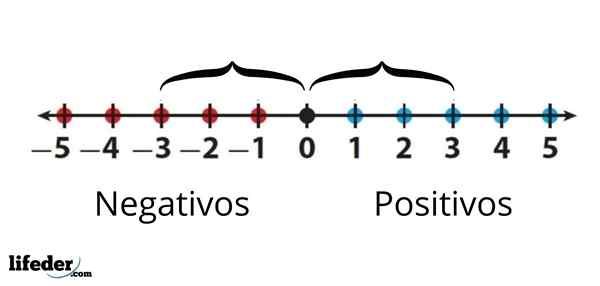Wartość bezwzględna -3 jest równa wartości bezwzględnej +3, ponieważ odległość między dowolnym do 0 jest taka sama

Podsumowując, wartość bezwzględna liczby jest tą samą liczbą liczby, ale zawsze z dodatnim znakiem.

Właściwości wartości bezwzględnej

Definicja wartości bezwzględnej

Główne właściwości wartości bezwzględnej:

• 1) Wartość bezwzględna liczby jest zawsze dodatnia lub 0, dlatego:

│x│≥ 0

• 2) Wartość bezwzględna zero wynosi również zero, czyli │0│ = 0, dlatego można potwierdzić, że:

│x│ = 0, tak y tylko wtedy, gdy x = 0

• 3) Dla każdej liczby x należy do zestawu liczb rzeczywistych, wartość bezwzględna x jest równa wartości bezwzględnej - x:

│x│ = │ - x│

• 4) Jeśli wartość bezwzględna liczby x wynosi a, oznacza to, że istnieją dwie opcje dla tej liczby: i) x = +a lub ii) x = -a.

Może ci służyć: Mary podróżuje 2/4 Cyclepist, Melissa podróżuje 4/8, a Anahi podróżuje 3/6

Na przykład, jeśli wartość bezwzględna liczby wynosi 5, dwie możliwości są takie, że liczba to +5 lub -5.

Operacje o wartości bezwzględnej

Następujące właściwości są bardzo przydatne do wykonywania operacji o wartościach bezwzględnych:

• 5) W przypadku „x” i „y”, które są dwiema liczbami rzeczywistymi, następujące nierówności są zawsze spełnione, nazywane trójkątna nierówność wartości bezwzględnej:

│x│+│y│≥ │x+y│

Na przykład bądź:

x = -6

y = 9

Lewa strona nierówności jest:

│-6│ + │9│ = 6 + 9 = 16

A prawa strona to:

│-6+9│ = │3│ = 3

Oczywiście 16 jest większe lub równe 3, i zawsze tak jest, gdy liczby x i mają różne znaki. Jeśli mają równe znaki, uzyskuje się równość. Zobacz ten inny przykład z dwoma innymi różnymi wartościami:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3 ≥│-8│

Rzeczywiście:

8 = 8

• 6) Produkt odpowiednich wartości bezwzględnych dwóch liczb rzeczywistych „x” i „y” jest równy wartości bezwzględnej iloczyn liczb:

│x│ ∙ │y│ = │x ∙ y│

Znowu są wartości:

x = -6

y = 9

Więc:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Co jest równe:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) iloraz wartości bezwzględnej dwóch liczb rzeczywistych „x” i „y”, z różnym mianownikiem 0, jest wartością bezwzględną ilorazu między tymi liczbami:

Tak długo, jak i ≠ 0.

Przykład:

Przykłady wartości bezwzględnej

Proste przykłady

Obliczenie wartości bezwzględnej dowolnej liczby rzeczywistych jest bardzo proste, na przykład wartość bezwzględna następujących liczb to:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Obliczenia o wartości bezwzględnej liczby rzeczywistej

Wykonaj następujące operacje, które obejmują wartość bezwzględną:

a) 2⋅│8│ + 5⋅│ -16│ --⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Może ci służyć: połowa 15

Jest to połączona operacja, więc preferowane jest jej rozwiązanie za pomocą kroków. Pierwsza wartość bezwzględna to:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

Druga wartość bezwzględna, która się pojawia, jest obliczana w następujący sposób:

│81 ÷ (-3) │ = │-27│ = 27

Następnie uzyskane wyniki są gromadzone i przeprowadzane są ostateczne obliczenia:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

Odległość między dwoma punktami na prawdziwej linii

Wartość bezwzględna pojawia się w wielu aplikacjach, takich jak znalezienie odległości między dwiema liczbami należącymi do linii rzeczywistej. Jeśli a jest liczbą rzeczywistą, znajduje się on na linii rzeczywistej w punkcie, którego odcięta jest „a”, to samo dzieje się z liczbą b.

Niech „A” i „B” na linii rzeczywistej, odległość, która je oddziela, to:

D_Ab = │B - a│

Które można również obliczyć przez:

D_Ab = │a - b│

Na przykład odległość między a = 5 i b = 12 to:

D = │5-12│ = │12-5│ = 7

W ten sposób wartość bezwzględna odejmowania między dwiema liczbami rzeczywistymi to po prostu odległość, która oddziela je na linii rzeczywistej.

Funkcja wartości bezwzględnej

Funkcja wartości bezwzględnej to aplikacja, która trafia na zestaw liczb rzeczywistych ℛ do ℛ⁺, co odpowiada każdej liczbie rzeczywistej jej wartości bezwzględnej. Jest zdefiniowany przez:

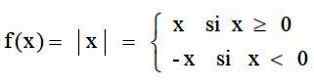
A jego wykres ma typową formę V:

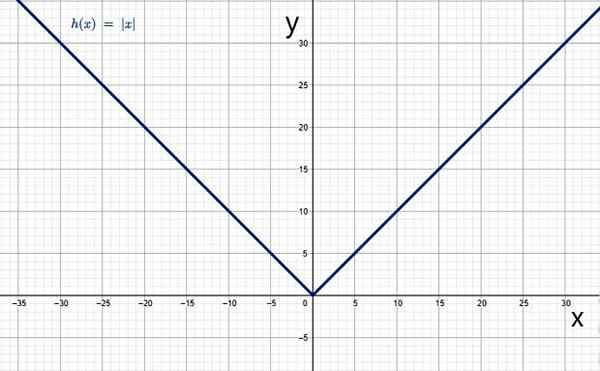Wartość bezwzględna jako funkcja. Źródło: f. Zapata przez Geogebra.

Charakterystyka funkcji wartości bezwzględnej

-Twoja domena jest zestawem wszystkich liczb rzeczywistych.

-Jest ciągły.

-Jest nawet, ponieważ jest spełnione, że f (x) = f (-x), dlatego osi pionowy jest osą symetrii.

-Zakres funkcji wartości bezwzględnej jest zbiorem pozytywnych rzeczywistych, w tym 0, ponieważ funkcja zawsze reprezentuje odległość, i jest to zawsze pozytywne lub zerowe.

Może ci służyć: jakie są wytyczne? (Geometria)

-Jest to funkcja według sekcji lub części.

-Zmniejsza się w przedziale (-∞, 0) i rośnie w (0,+∞).

Argument wartości bezwzględnej może być również funkcją kwadratową lub inną, na przykład można ją zdefiniować:

• f (x) = │x²-5x+3│
• g (x) = │Sen x│

Wartość bezwzględna jest odpowiedzialna za pozytywowanie obrazów argumentu, które mają znak ujemny.

Rozwiązane ćwiczenia

Ćwiczenie 1

Oceń następujące wyrażenia algebraiczne o wartości bezwzględnej:

a) │2x -5│ + │ --x + 1│ at x = 3

b) │ (x - 5) ÷ (x+4) │ at x = −1

Rozwiązanie

│2⋅3-5│ + │ - 3 + 1│ = │6-5│ + │ - 2│ = │1│ + 2 = 3

Rozwiązanie b

│ (-1–5) ÷ (-1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Ćwiczenie 2

Jaki jest zestaw wartości reprezentujących następującą nierówność?

│x│≤ 3

Rozwiązanie

Nierówność reprezentuje wszystkie liczby rzeczywistych, których wartość bezwzględna jest mniejsza lub równa 3, dlatego jest to zestaw wszystkich liczb między -3 do +3, w tym te.

W notacji interwałowej pozostaje:

[-3,3]

Ćwiczenie 3

Rozwiąż następujące równanie o wartości bezwzględnej:

│2x-1│ = 5

Rozwiązanie 

Jak wskazano wcześniej, aby rozwiązać równanie o wartości bezwzględnej, należy rozważyć dwie opcje. Mam na myśli, tak:

│f (x) │ = c

Więc:

1) f (x) = c

2) f (x) = -C

Dlatego to równanie, którego argument jest liniowy, ma dwa rozwiązania:

Pierwsze rozwiązanie

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Drugie rozwiązanie

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Podczas oceny x₁ = 3 lub x₂ = -2 W pierwotnym równaniu należy uzyskać równość, w ten sposób weryfikuje się, że uzyskane wartości są rozwiązaniem proponowanego równania. Rzeczywiście:

│ (2⋅3) -1│ = │6-1│ = 5

A podczas próbowania z drugą opcją uzyskuje się również równość:

│2⋅ (-2) -1│ = │-4-1│ = 5

Bibliografia

1. Baldor, a. 2005. Algebra. Grupa kulturowej ojczyzny.
2. Larson, r. 2012. Przedłużanie. 8. Wydanie. Cengage Learning.
3. Hoffman, J. Wybór problemów z matematyką. Głośność 2.
4. Stewart, J. 2007. Prefrecment: Matematyka do obliczania. 5. Wydanie. Cengage Learning.
5. Zill, d. 1984. Algebra i trygonometria. McGraw Hill.