A romboid Jest to płaska postać czterech stron, -A czworobok -in, w którym jego boki i wewnętrzne kąty są różne od dwóch do dwóch. Dlatego romboid należy do grupy ukośnych równoległoboków.

Liczby geometryczne są częścią natury, a zwłaszcza czterech stron, takich jak Rhomboid, mają wiele zastosowań w architekturze i projektowaniu.

Rysunek 1. Panele oświetleniowe stadionu Allianz Arena w Monachium w Niemczech, oświetlone kolorami lokalnego zespołu i białym światłem, gdy wybór tego kraju gra. Źródło: Pxhere.

Mamy część fasady stadionu piłkarskiego Allianz Arena w Monachium. Są to panele Rhomboid, które rozświetlają kolory lokalnego zespołu.

Jest to zatem postać o dużej dynamizmie wizualnej, ponieważ w przeciwieństwie do innych czworoboku, nie ma osi symetrii. Poniższy rysunek pokazuje różne romboidy z różnorodnymi orientacjami w płaszczyźnie.

Rysunek 2. Kilka romboidów z różnymi orientacjami w płaszczyźnie. Źródło: f. Zapata.

[TOC]

Charakterystyka Romboid

Następnie główne cechy tego interesującego geometrycznego rysunku:

-Numer arkusza: 4.

-Liczba wierzchołków: 4.

-Przeciwne strony są takie same i równoległe, jednak sąsiednie strony są nierówne.

-Ma 4 wewnętrzne kąty: dwa ostre (mniejsze niż 90º), oznaczone grecką literą α i dwa tępe (ponad 180º), zwane β (patrz ryc. 3).

-Dodając dwa ciągłe kąty romboida, otrzymuje się 180º, dlatego α i β są Uzupełniający.

-Suma 4 kątów wewnętrznych wynosi 360º.

-Przekątna to segment, który zaczyna się od wierzchołka i kończy się na przeciwnym wierzchołku.

-Punkt, w którym nazywane jest przecięcie romboida przecinającego się BaryCenter.

-Przekąski Rhomboid mają różne rozmiary.

O przekątkach Rhomboid, istnieją kilka ważnych szczegółów, które omówimy poniżej.

Może ci służyć: w oczekiwaniu na wiersz: wzór i równania, reprezentacja, przykłady

Piagonals of the Rhomboid

Bardzo ważne jest, aby podkreślić, że przekąski romboidów nie są bisektyczne, to znaczy nie dzielą wewnętrznych kąty figury na dwie równe części.

Przekąski nie są do siebie prostopadłe. Możemy jednak łatwo je obliczyć za pomocą twierdzenia cosinus. Zatem główna przekątna d_M W Rhomboid z ryc. 3 to:

D_M = √ (a² + B² - 2.Ab.cos β)

I drobna przekątna d_M Byłbym:

D_M = √ (a² + B² - 2.Ab.cos α)

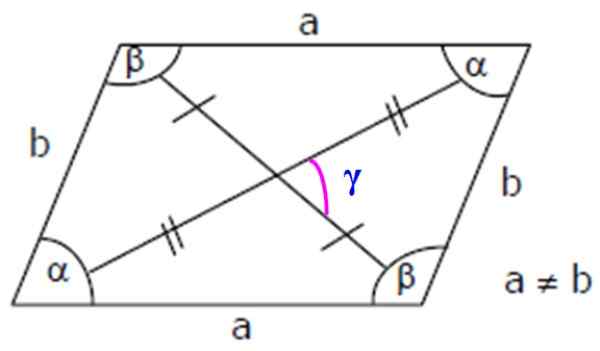Rysunek 3. Romboid Elementy: strony, wewnętrzne i ukośne kąty. Źródło: Wikimedia Commons.

Ważny: Ponieważ α i β są uzupełniające, spełnia się, że:

sin α = sin β

COS α = -COS β

Te właściwości przyczyn trygonometrycznych należy wziąć pod uwagę przy rozwiązywaniu ćwiczeń.

Jak wyjąć obwód i obszar

Aby znaleźć obwód i obszar, nadajemy nazwę bokom Rhomboid, to będzie Do I B. Mamy również wysokość Rhomboid, o nazwie H, która jest linią wyciągniętą z jednego z wierzchołków i skierowana prostopadle do przeciwnej strony figury.

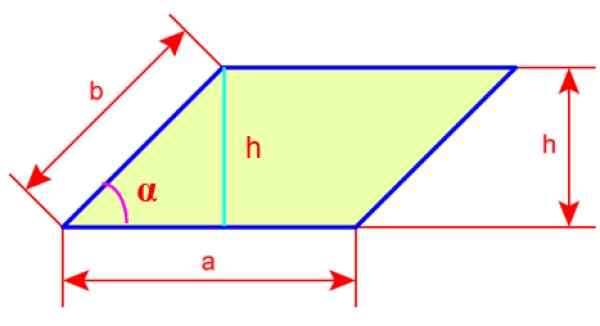Rysunek 4. Boki i wysokość Rhomboid. Źródło: Wikimedia Commons.

Obwód Rhomboid

Obwód Rhomboid jest obliczany przez dodanie długości jego czterech stron. Zadzwoń na P na obwodzie, więc:

P = 2a + 2b

Możemy to również wyrazić przez:

P = 2 (A+B)

Obwód znający wysokość

Jeśli będziemy dobrze wyglądać, wysokość H można określić na podstawie trójkąta po lewej stronie na rycinie 4. Strona B byłaby hipotencja i wysokość H Cateto przeciwna kątowi α, dlatego:

sin α = przeciwny / hipotenusa cateto

O Cóż:

sin α = h / b

Następnie wyczyścimy B:

B = h / sin α

Wymieniamy się na obwodzie P:

P = 2 [a + (h / sin α)]

Obszar Romboid

Obszar Rhomboid jest miarą jego powierzchni. A ponieważ jest to równoległobok, jego obszar A jest podany przez dobrze znane wyrażenie:

Może ci służyć: wspólny czynnik grupowania warunków: przykłady, ćwiczenia

A = podstawa x wysokość

Że zgodnie z rysunkami 3 i 4 jest wyrażane przez:

A = a x h

Obszar znający obie strony i kąt wewnętrzny

Stosując podstawową trygonometrię poprzedniej sekcji, znajdujemy równoważne wyrażenia dla obszaru Rhomboid:

H = b. sin α

Wtedy obszar jest taki:

A = a. B. sin α

Pamiętając o tym, co powiedzieliśmy powyżej o kątach uzupełniających, w razie potrzeby możemy zastąpić SEN α ​​SEN β.

Obszar znający przekątę i kąt między nimi

Wreszcie, jeśli znamy przekąski d_M i d_M, Plus kąt γ między nimi (patrz ryc. 3), powierzchnię można obliczyć za pomocą półprodukta przekątnego przez piersią wspomnianego kąta:

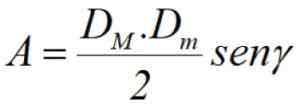
Ćwiczenie rozwiązane

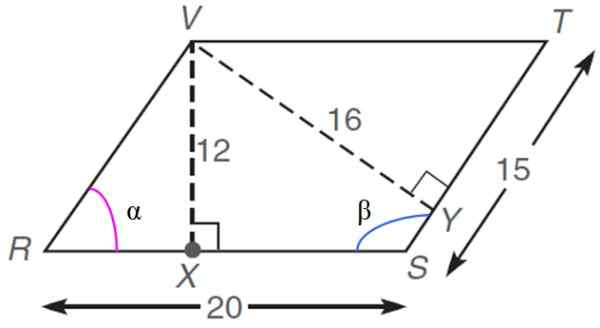
W następujących Rhomboid, których wymiary podano w dowolnych jednostkach lub.Do., znajdować:

a) wartość obwodu

b) obszar

c) Kąty wewnętrzne α i β

d) długość segmentu Rx

e) miara każdej z przekątnych

Rozwiązanie

Obwód P to:

P = 2 (A + B)

Najpierw identyfikujemy wartości A i B:

A = 20

B = 15

Wymieniamy wzór i obliczamy:

P = 2. (20 + 15) = 70 u.Do.

Rozwiązanie b

Schemat zapewnia wysokość h = 12 u.A Dlatego obszar można obliczyć za pomocą wzoru:

A = a x h

A = 20 x 12 u.Do.² = 240 u.Do.²

Niezależnie od wybranej jednostki do pomiaru boków i wysokości, obszar jest zawsze wyrażany w kwadratowych jednostkach.

Ten sam wynik, jeśli otrzymasz przy obliczaniu obszaru z inną wysokością Rhomboid, który jest wart 16 U.Do. Rzeczywiście:

A = 16 x 15 u.Do.² = 240 u.Do.²

Rozwiązanie c

Kąt α można obliczyć:

Może ci służyć: środki pozycji, centralna tendencja i dyspersja

H = b. sin α

Ponieważ wartości H i B są znane, zatem:

α = arcsen (h/b) = arcsen (12/15) = 53.13

Pamiętając, że kąty α i β są uzupełniające, jest spełnione:

α + β = 180º ⇒ β = 180–53.13. = 126.87º

Rozwiązanie d

Długość segmentu RX jest łatwo obliczona, ponieważ jest wystarczająca ilość informacji, aby je znaleźć. Na przykład::

Rx = rv . cos α = 15 . Cos 53.13. U.Do. = 9 u.Do.

Także przez twierdzenie Pitagorasa przez prostokątowy trójkąt boków 15 i 12 u.Do:

(RV)² = (Rx)² + H²

Oczyszczanie długości segmentu odsetek:

Rx = √ [(rv)² - H²] = √ [15² - 12²] = √81 = 9

Rozwiązanie e

Miara jednej z przekątnej, na przykład przekątnej, która łączy wierzchołki R i T, co jest główną przekątną, jest podawana przez twierdzenie cosinus, jak wyjaśniono wcześniej, więc zastępujemy tam wartości:

D_M = √ (20² + 25² - 2. 20. piętnaście .Cos 126.87º) = 37.22 u.Do.

Dla mniejszej diagonalnej:

D_M = √ (20² + 25² - 2. 20. piętnaście .Cos 53.13) = 25.79 u.Do.

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Baldor, a. 1973. Geometria i trygonometria. Redakcja kulturalna Ameryki Środkowej.
3. I. DO. 2003. Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
4. Jiménez, r. 2010. Matematyka II. Geometria i trygonometria. Druga edycja. Prentice Hall.
5. Zwykłe wielokąty. Wyzdrowiał od: kolego.Inżynieria.USAC.Edu.Gt.
6. Formuły wszechświata. Romboid. Odzyskane z: Universoformulas.com.
7. Wikipedia. Romboid. Odzyskane z: jest.Wikipedia.org.