Trójkąt równoramienny

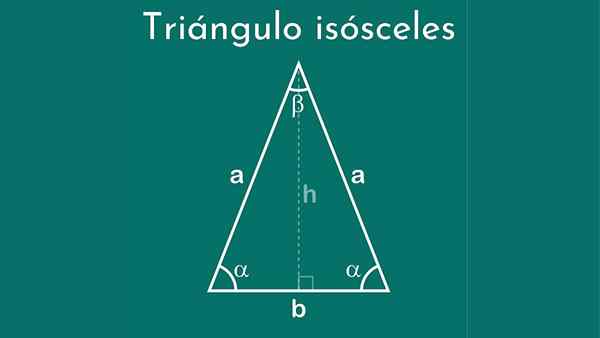
Trójkąt Isosceles ma dwie równe strony i jedną różne

Co to jest trójkąt Isosceles?

A Trójkąt równoramienny Jest to wielokąta trójokąta, w którym dwie z nich mają tę samą miarę, a trzecia strona inna miara. Ta ostatnia strona nazywa się bazą. Ze względu na tę cechę podano tę nazwę, która w grecku oznacza „równe nogi”.

Trójkąty to wielokąty uważane za najprostsze w geometrii, ponieważ są one tworzone przez trzy strony, trzy kąty i trzy wierzchołki. To oni mają najmniejszą liczbę stron i kątów w odniesieniu do innych wielokątów, jednak ich użycie jest bardzo obszerne.

Charakterystyka trójkątów Isosceles

Trójkąt Isosceles został sklasyfikowany przy użyciu miary jego boków jako parametru, ponieważ dwie jego boki są zgodne, to znaczy mają tę samą długość.

Zgodnie z amplitudą kątów wewnętrznych trójkąty Isosceles są klasyfikowane jako:

• Isosceles Trójkąt prostokąta: Dwie jego strony są takie same. Jeden z jego kątów jest prosty (90^albo), A pozostałe są takie same (45^albo każdy)
• Isosceles tępy trójkąt: Dwie jego strony są takie same. Jeden z jego kątów jest tępy (> 90^albo).
• Isosceles Trójkąt Acutangle: Dwie jego strony są takie same. Wszystkie jego kąty są ostre (< 90^albo), Gdzie dwa mają tę samą miarę.

składniki

• Mediana: Jest to linia, która odchodzi z punktu środkowego z jednej strony i osiąga przeciwny wierzchołek. Trzy media uczestniczą w punkcie o nazwie Barcentro lub Centroid.
• Bisektor: Jest to pół -prawe, które dzieli kąt każdego wierzchołka na dwa kąty równej miary. Dlatego jest znany jako oś symetrii, a ten typ trójkątów ma tylko jeden.
• MediaTrix: Jest to segment prostopadły do ​​boku trójkąta, który pochodzi z tego środka. W trójkącie są trzy mediaci i uczestniczą w punkcie o nazwie CircCentro.
• Wysokość: To linia przechodzi od wierzchołka do boku, która jest przeciwna, a także ta linia jest prostopadła do tej strony. Wszystkie trójkąty mają trzy wysokości, które pokrywają się w punkcie zwanym Ortocenter.

Isosceles Trójkąty właściwości

Isosceles trójkąty są zdefiniowane lub zidentyfikowane, ponieważ mają one kilka reprezentowanych przez nich właściwości, pochodzących z twierdzeń zaproponowanych przez wielkich matematyków:

Kąty wewnętrzne

Suma kątów wewnętrznych jest zawsze równa 180^albo.

Suma boków

Suma miar dwóch stron powinna być zawsze większa niż miara trzeciej strony, a + b> c.

Przystające strony

Isosceles Trójkąty mają dwie strony o tej samej miary lub długości; to znaczy są przystające, a trzecia strona różni się od tych.

Przystające kąty

Trójkąty Isosceles są również znane jako izoangalne trójkąty, ponieważ mają dwa kąty, które mają tę samą miarę (przystające). Znajdują się u podstawy trójkąta, w przeciwieństwie do boków, które mają tę samą długość.

Może ci służyć: trapezoidalny pryzmat

Z tego powodu twierdzenie, które to określa:

„Jeśli trójkąt ma dwie przystające strony, kąty przeciwne tych stron również będą zgodne”. Dlatego jeśli trójkąt jest izosceles, kąt jego baz są przystające.

Przykład:

Na poniższym rysunku obserwuje się trójkąt ABC. Podczas rysowania bisektora z wierzchołka kąta B do podstawy trójkąt jest podzielony na dwa trójkąty BDA i BDC:

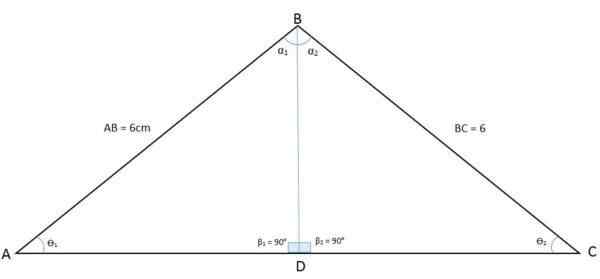Bisektor, który dzieli się na dwa trójkąty równe trójkącie Isosceles

W ten sposób kąt wierzchołka B został również podzielony na dwa równe kąty. Bisektor jest teraz wspólną stroną (BD) między tymi dwoma nowymi trójkątami, podczas gdy strony AB i BC są zgodnymi stronami. Taka jest przypadek boku, kąt, boku (LAL).

To pokazuje, że kąty wierzchołków A i C mają tę samą miarę, a także można wykazać, że ponieważ trójkąty BDA i BDC są zgodne, strony AD i DC są również strony AD i DC.

Wysokość, mediana, meditrix i bisektor są przypadkowe

Linia wyciągnięta z wierzchołka przeciwna do podstawy do punktu środkowego podstawy trójkąta, jest jednocześnie wysokość, mediana i meditrix, a także bisektor w stosunku do przeciwnego kąta podstawy.

Wszystkie te segmenty pokrywają się w tym, który je reprezentuje.

Przykład:

Na poniższym rysunku trójkąt ABC obserwuje się ze średnim punktem M, który dzieli podstawę na dwa segmenty BM i CM.

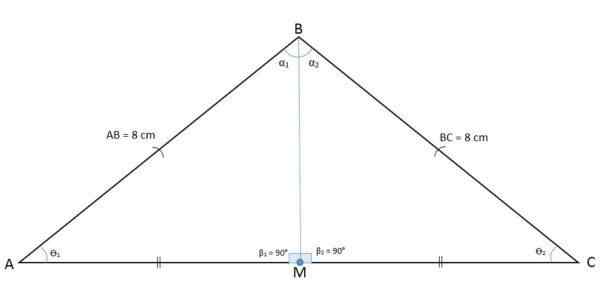Wysokość, mediana, meditrix i bisektor są przypadkowe

Podczas rysowania odcinka od punktu M do przeciwnego wierzchołka, z definicji uzyskuje się medianę AM, która jest względna wierzchołka A i strony BC.

Ponieważ segment AM dzieli trójkąt ABC na dwa równe trójkąty AMB i AMC, oznacza to, że przypadek boku, kąta, boku, a zatem AM będzie również dwusektorem Bâc.

Dlatego bisektor zawsze będzie równy medianie i odwrotnie.

Segment AM tworzy kąty, które mają tę samą miarę dla trójkątów AMB i AMC; to znaczy, że są one uzupełniające, tak że miarę każdego z nich będzie:

Med. (Amb) + med. (AMC) = 180^albo

2 _* Med. (AMC) = 180^albo

Med. (AMC) = 180^albo ÷ 2

Med. (AMC) = 90^albo

Można wiadomo, że kąty utworzone przez segment AM dotyczące podstawy trójkąta są proste, co wskazuje, że ten segment jest całkowicie prostopadły do ​​podstawy.

Dlatego reprezentuje wysokość i mediaTrix, wiedząc, że M jest punktem środkowym.

Dlatego linia AM:

• Reprezentuje wysokość BC.
• Jest średniej wielkości.
• Jest zawarty w BC MediaTrix.
• Jest to dwusa'a kąta wierzchołka â

Względne wysokości

Wysokości w stosunku do równych stron mają również tę samą miarę.

Może ci służyć: Idealne liczby: Jak je zidentyfikować i przykłady

Ponieważ trójkąt Isosceles ma dwie równe strony, jego dwie odpowiednie wysokości będą również takie same.

Orocentro, Barcentro, Inntro i Colecendro Coinsides

Ponieważ wysokość, mediana, dwusektora i meditrix związane z bazą są jednocześnie reprezentowane przez ten sam segment, ortocenter, barycentro, zachęta i obwód będą punktami kolineal, to znaczy można je znaleźć w tej samej linii:

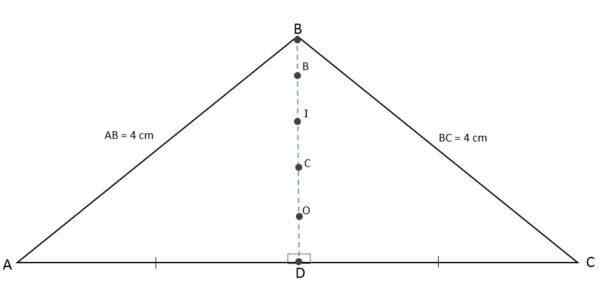Ortocenter, Barcentro, Inntro i Circcentro są również przypadkowe

Obliczanie trójkątów Isosceles

Jak obliczyć obwód?

Obwód wielokąta jest obliczany przez sumę boków.

Ponieważ w tym przypadku trójkąt izosceles ma dwie strony o tej samej miarę, jego obwód jest obliczany za pomocą następującego wzoru:

P = 2_*(strona a) + (strona b).

Jak obliczyć wysokość?

Wysokość jest linią prostopadłą do podstawy, dzieli trójkąt na dwie części równe, rozciągając się na przeciwny wierzchołek.

Wysokość reprezentuje przeciwne Cateto (A), połowa podstawy (B/2) do sąsiedniego Cateto, a strona „A” reprezentuje hipotencję.

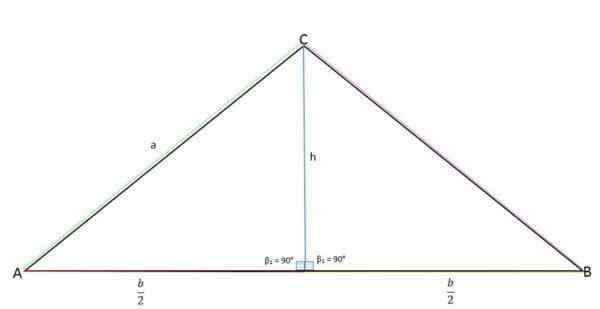Obliczanie wysokości trójkąta Isosceles

Za pomocą twierdzenia Pitagorasa można określić wartość wysokości:

Do² + B² = C²

Gdzie:

Do² = wysokość (h).

B² = B / 2.

C² = strona a.

Zastępując te wartości w twierdzeniu Pitagoras i wyczyszczenie wysokości, jaką masz:

H² + (B / 2)² = Do²

H² + B² / 4 = Do²

H² = Do² - B² / 4

H = √ (Do² - B² / 4).

Jeśli kąt utworzony przez przystające strony jest znany, wysokość można obliczyć za pomocą następującego wzoru:

Jak obliczyć obszar?

Trójkąty są zawsze obliczane z tym samym wzorem, mnożąc podstawę według wysokości i dzieląc przez 2:

Są przypadki, w których znane są tylko miary dwóch stron trójkąta, a kąt utworzony między nimi. W takim przypadku, aby określić obszar, którego konieczne jest zastosowanie powodów trygonometrycznych:

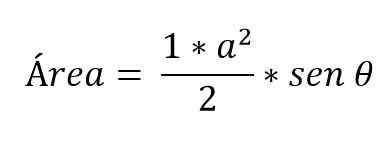
Jak obliczyć podstawę trójkąta?

Ponieważ trójkąt Isosceles ma dwie równe strony, aby określić wartość jej podstawy, konieczne jest znanie przynajmniej miary wysokości lub jednego z jej kąta.

Znając wysokość, stosuje się twierdzenie Pitagorasa:

Do² + B² = c²

Gdzie:

Do² = wysokość (h).

C² = strona a.

B² = B / 2, jest nieznany.

Oczyszczamy b² Formuły i musimy:

B² = a² - C²

B = √ a² - C²

Ponieważ wartość ta odpowiada połowy podstawy, należy ją pomnożyć przez 2, aby uzyskać pełną miarę podstawy trójkąta Isosceles:

B = 2 _* (√ a² - C²)

W przypadku, gdy znana jest tylko wartość jego równych stron i kąt między nimi, stosuje się trygonometrię, rysując linię z wierzchołka do podstawy, która dzieli trójkąt Isosceles na dwa prostokąty trójkąty.

W ten sposób połowa podstawy jest obliczana za pomocą:

Wartość wysokości i kąt wierzchołka, który jest również przeciwny podstawowi. W takim przypadku za pomocą trygonometrii można ustalić podstawę:

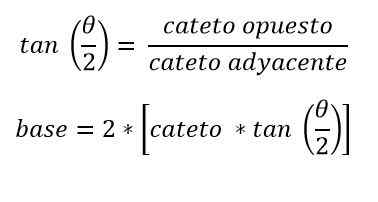
Ćwiczenia

Pierwsze ćwiczenie

Znajdź obszar Isosceles ABC Triangle, wiedząc, że dwie z jego boków mierzą 10 cm, a trzecia strona mierzy 12 cm.

Może ci służyć: antykiwatywne: formuły i równania, przykłady, ćwiczenia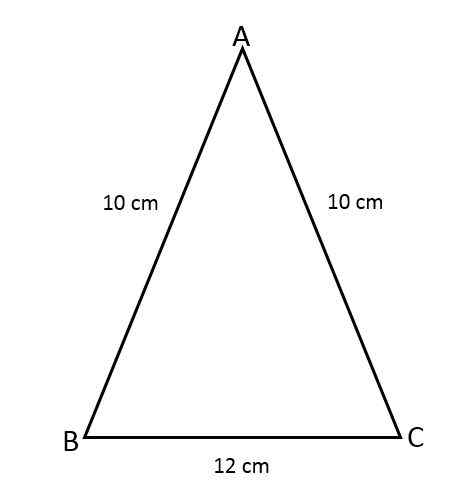

Rozwiązanie

Aby znaleźć obszar trójkąta, konieczne jest.

Dostępne są następujące dane Isosceles Triangle:

• Równe strony (a) = 10 cm.
• Podstawa (b) = 12 cm.

Wartości są zastępowane w wzorze:

Drugie ćwiczenie

Długość dwóch równych stron trójkąta izoscelesowego mierzy 42 cm, związek tych stron tworzy kąt 130^albo. Określ wartość trzeciej strony, obszar tego trójkąta i obwodu.

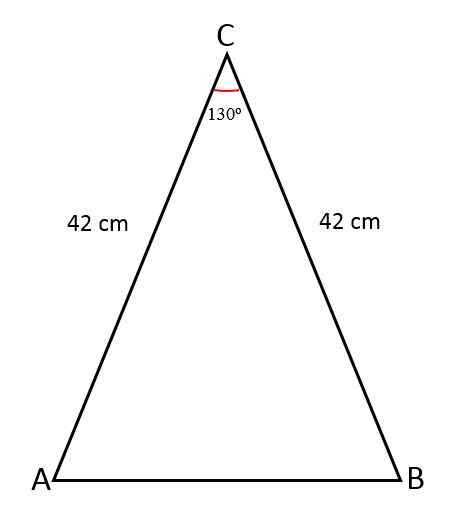
Rozwiązanie

W tym przypadku znane są pomiary boków i kąt.

Aby poznać wartość brakującej strony, to znaczy podstawa tego trójkąta, linia prostopadła do niej jest narysowana, dzieląc kąt na dwie równe części, po jednym dla każdego uformowanego trójkąta prostokąta.

• Równe strony (a) = 42 cm.
• Kąt (ɵ) = 130^albo

Teraz, za pomocą trygonometrii, obliczana jest wartość połowy podstawy, która odpowiada połowy hipotenu:

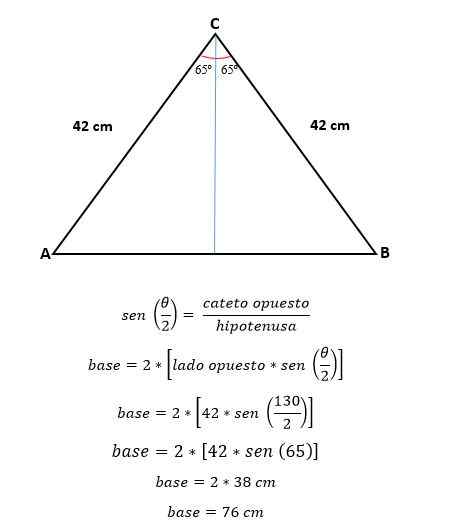
Aby obliczyć obszar, należy znać wysokość tego trójkąta, który można obliczyć za pomocą trygonometrii lub twierdzenia Pitagorasa, teraz, gdy wartość podstawy była już określona.

Trygonometrią będzie:

Obwód jest obliczany:

P = 2_*(strona a) + (strona b).

P = 2_* (42 cm) + (76 cm)

P = 84 cm + 76 cm

P = 160 cm.

Trzecie ćwiczenie

Oblicz wewnętrzne kąty trójkąta Isosceles, wiedząc, że kąt podstawy wynosi â = 55^albo

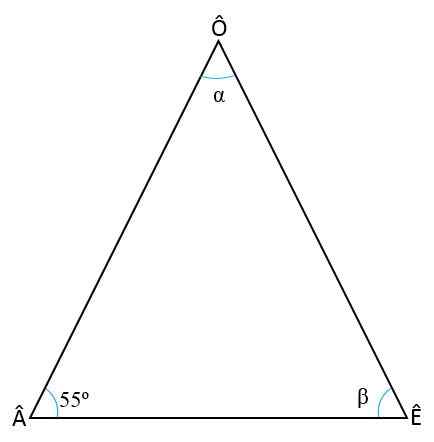
Rozwiązanie

Aby znaleźć dwa brakujące kąty (ê i ô), należy pamiętać o dwóch właściwościach trójkątów:

• Suma wewnętrznych kątów każdego trójkąta będzie zawsze = 180^albo:

 + ê + ô = 180 ^albo

• W trójkącie Isosceles kąty podstawy są zawsze przystające, to znaczy mają tę samą miarę, dlatego:

 = ô

Ê = 55^albo

Aby określić wartość kąta ê, wartości innych kątów w pierwszej regule są zastąpione, a ê jest wyczyszczony:

55^albo + 55^albo + Ô = 180 ^albo

110 ^albo + Ô = 180 ^albo

Ô = 180 ^albo - 110 ^albo

Ô = 70 ^albo.

Bibliografia

1. Álvarez, e. (2003). Elementy geometrii: z licznymi ćwiczeniami i geometrią kompasu. University of Medellin.
2. Álvaro rendón, do. R. (2004). Rysunek techniczny: Notatnik aktywności.
3. Anioł, a. R. (2007). Algebra podstawowa. Edukacja Pearsona.
4. Arthur Goodman, L. H. ( 1996). Algebra i trygonometria z geometrią analityczną. Edukacja Pearsona.
5. Baldor, a. (1941). Algebra. Hawana: Kultura.
6. José Jiménez, L. J. (2006). Matematyka 2.
7. Tuma, J. (1998). Podręcznik matematyki inżynierii. Wolfram Mathworld.