Trójkąt skalene
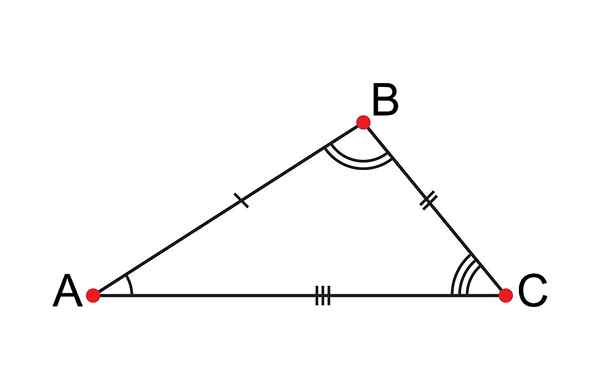
- 1235
- 212
- Bertrand Zawadzki
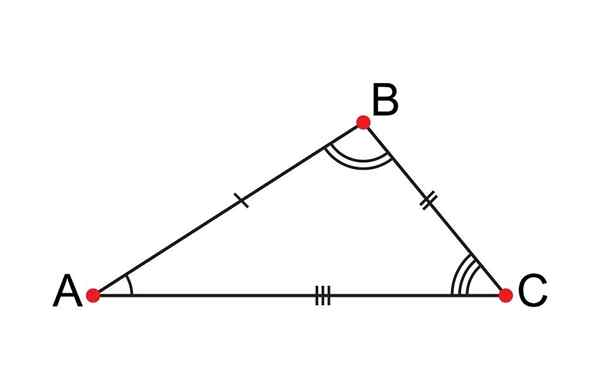 Trójkąt skalene ma wszystkie nierówne strony
Trójkąt skalene ma wszystkie nierówne strony Co to jest trójkąt skaleny?
A Trójkąt skalene Jest to wielokąt trzyosobowy, w którym każdy ma inne pomiary lub długości; Z tego powodu otrzymał nazwę Escaleno, co po łacinie oznacza nierówne.
Trójkąty są wielokątami uważanymi za najprostsze w geometrii, ponieważ powstają trzy strony, trzy kąty i trzy wierzchołki. W przypadku trójkąta skalen.
Charakterystyka trójkątów skali
Trójkąty skalne są prostymi wielokątami, ponieważ żadna z jego boków ani kątów nie ma takiej samej miary, w przeciwieństwie do izosceli i trójkątów równowagi.
Ponieważ wszystkie ich boki i kąty mają różne pomiary, te trójkąty są uważane za nieregularne wypukłe wielokąty.
Zgodnie z amplitudą kątów wewnętrznych trójkąty skalene są klasyfikowane jako:
- Trójkąt prostokąta skalene: Wszystkie jego strony są różne. Jeden z jego kątów jest prosty (90albo), a pozostałe są ostre i mają różne miary.
- Trójkąt Scalene tępy: Wszystkie jego boki są różne, a jeden z jego kątów jest tępy (> 90albo).
- Scalene Acutangle Triangle: Wszystkie jego strony są różne. Wszystkie jego kąty są ostre (< 90albo), Z różnymi miarami.
Kolejną cechą trójkątów skalen.
Komponenty/elementy
Mediana
Jest to linia, która odchodzi z punktu środkowego z jednej strony i osiąga przeciwny wierzchołek. Trzy media uczestniczą w punkcie o nazwie Barcentro lub Centroid.
Bisektor
Jest to pół -prawe, które dzieli każdy kąt na dwa kąty równej miary. Bisektory trójkąta zgadzają się w punkcie zwanym zachęcie.
MediaTrix
Jest to segment prostopadły do boku trójkąta, który pochodzi z tego środka. W trójkącie są trzy mediary i uczestniczą w punkcie o nazwie CircCentro.
Wysokość
To linia przechodzi od wierzchołka na przeciwną stronę, a także ta linia jest prostopadła do tej strony. Wszystkie trójkąty mają trzy wysokości, które pokrywają się w punkcie o nazwie Ortotenter.
Właściwości trójkąta Escaleno
Trójkąty skalne są zdefiniowane lub zidentyfikowane, ponieważ mają one kilka reprezentujących je właściwości, pochodzące z twierdzeń zaproponowanych przez wielkich matematyków. Oni są:
Kąty wewnętrzne
Suma kątów wewnętrznych jest zawsze równa 180albo.
Suma boków
Suma miar dwóch stron powinna być zawsze większa niż miara trzeciej strony, a + b> c.
Nieprawidłowe strony
Wszystkie strony trójkątów wspinaczkowych mają różne miary lub długości; to znaczy są niespójni.
Niezgodne kąty
Ponieważ wszystkie boki trójkąta skalene są różne, jego kąty będą również. Jednak suma kątów wewnętrznych będzie zawsze równa 180º, aw niektórych przypadkach jeden z jego kąta może być tępy lub prosty, podczas gdy w innych wszystkie jego kąty będą ostre.
Może ci służyć: problemy z multiplikatywnymi dla dzieci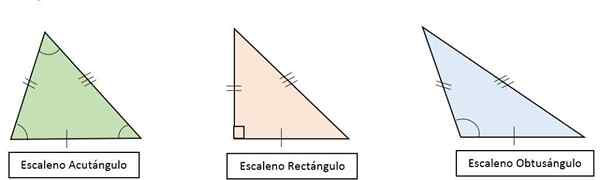 Rodzaje trójkątów Scalele zgodnie z ich kątami
Rodzaje trójkątów Scalele zgodnie z ich kątami Wysokość, mediana, meditrix i bisektor nie są przypadkowe
Jak każdy trójkąt, Escaleno ma różne linie, które go komponują, takie jak: wysokość, średnia, mediaTrix i bisektor.
Ze względu na szczególność jego boków, w tego typ.
Orocentro, Barcenentro, Inntentro i Circcentro nie są przypadkowe
Podobnie jak wysokość, mediana, dwusektor i mediaTix są reprezentowane przez różne segmenty linii, w trójkącie skaleniowym punkty spotkań -Orthocenter, Incentre i Circcentro Barcenter -w różnych punktach (to znaczy, że nie pokrywają się).
W zależności od tego, czy trójkąt jest acutangle, prostokąt lub tępy, ortocenter ma różne lokalizacje:
Do. Jeśli trójkąt jest acutangle, ortocenter będzie wewnątrz trójkąta.
B. Jeśli trójkąt jest prostokąta, ortocenter pokrywa się z wierzchołkiem po prostej stronie.
C. Jeśli trójkąt jest tępy, ootocenter będzie poza trójkątem.
Względne wysokości
Wysokości są w stosunku do boków.
W przypadku trójkąta skalenicznego wysokości te będą miały różne miary. Każdy trójkąt ma trzy względne wysokości i aby je obliczyć, stosuje się formułę Herón.
Obliczenie obwodu, powierzchnia, wysokość i boki
Jak obliczyć obwód?
Obwód wielokąta jest obliczany przez sumę boków.
Ponieważ w tym przypadku trójkąt skalene ma wszystkie swoje strony o innej miarę, jego obwód będzie:
P = strona z boku + strona B +.
Jak obliczyć obszar?
Trójkąty są zawsze obliczane za pomocą tego samego wzoru, mnożąc podstawę według wysokości i dzieląc przez dwa:
Obszar = (baza * H) ÷ 2
W niektórych przypadkach wysokość trójkąta skalene nie jest znana, ale istnieje formuła zaproponowana przez matematyka Heróna, aby obliczyć obszar znający miarę trzech stron trójkąta.
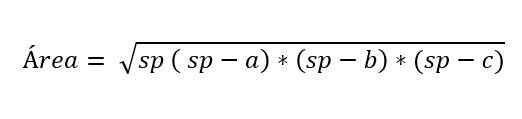
Gdzie:
- A, b i c reprezentują boki trójkąta.
- SP odpowiada pół -perymetrowi trójkąta, to znaczy połowa obwodu:
SP = (A + B + C) ÷ 2
W przypadku, gdy mają tylko dwie boki trójkąta i kąt, który powstaje między nimi, obszar można obliczyć, stosując przyczyny trygonometryczne. W ten sposób musisz:
Obszar = (strona * H) ÷ 2
Gdzie wysokość (h) jest produktem z jednej strony przez przeciwny kąt. Na przykład po każdej stronie obszar będzie:
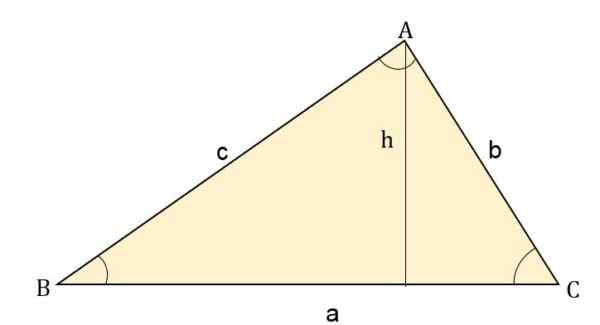
- Obszar = (b * C * sin a) ÷ 2
- Obszar = (a * C * sin b) ÷ 2.
- Obszar = (a * B * Sen C) ÷ 2
Jak obliczyć wysokość?
Podobnie jak wszystkie boki trójkąta skalenicznego, są różne, nie można obliczyć wysokości za pomocą twierdzenia Pitagorasa.
Z formuły Heróna, oparte na miarach trzech stron trójkąta, obszar można obliczyć.
Może ci służyć: notacja czynnikowa: koncepcja, przykłady i ćwiczeniaWysokość może być wyraźna z ogólnej formuły obszaru:
 Wzór do obliczenia wysokości trójkąta skalenicznego
Wzór do obliczenia wysokości trójkąta skalenicznego Strona jest zastąpiona miarą strony A, B lub C.
Innym sposobem obliczenia wysokości, gdy znana jest wartość jednego z kąta, jest stosowanie powodów trygonometrycznych, w których wysokość będzie reprezentować trójkąt Cateto.
Na przykład, gdy znany jest odwrotny kąt, zostanie on określony przez pierś:
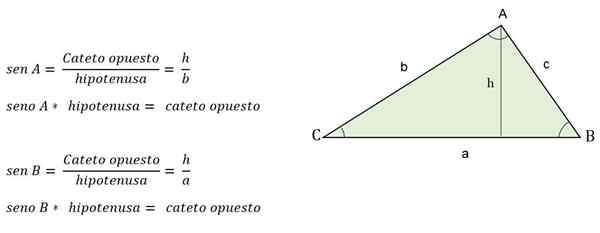 Formuła trygonometryczna do obliczenia wysokości trójkąta skalenicznego
Formuła trygonometryczna do obliczenia wysokości trójkąta skalenicznego Jak obliczyć boki?
Gdy masz miarę dwóch stron i kąt przeciwny, możliwe jest określenie trzeciej strony zastosowania twierdzenia Cosenos.
Na przykład w trójkącie AB rysowana jest wysokość względem segmentu prądu przemiennego. W ten sposób trójkąt jest podzielony na dwa trójkąty prostokąta.
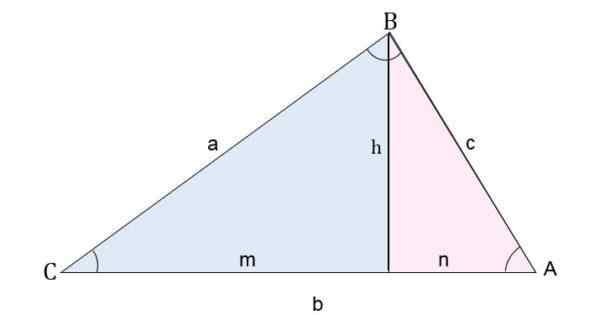 Podział trójkąta skalenicznego na dwa prostokąty w celu obliczenia boków
Podział trójkąta skalenicznego na dwa prostokąty w celu obliczenia boków Aby obliczyć stronę C (segment AB), zastosowano twierdzenie Pitagorasa dla każdego trójkąta:
- W przypadku niebieskiego trójkąta musisz:
C2 = h2 + M2
Jak M = B - N, jest zastępowany:
C2 = h2 + B2 (B - N)2
C2 = h2 + B2 - 2BN + N2.
- Aby uzyskać różowy trójkąt, musisz:
H2 = a2 - N2
Zostaje zastąpiony w poprzednim równaniu:
C2 = a2 - N2 + B2 - 2BN + N2
C2 = a2 + B2 - 2Bn.
Wiedząc, że n = a * COS C, jest zastępowany w poprzednim równaniu i uzyskuje się wartość strony C:
C2 = a2 + B2 - 2b* Do * cos c.
Zgodnie z prawem Cosenos boki można obliczyć jako:
- Do2 = b2 + C2 - 2b* C * rzeczy.
- B2 = a2 + C2 - 2* C * cos b.
- C2 = a2 + B2 - 2b* Do * cos c.
Są przypadki, w których miary boków trójkąta nie są znane, ale ich wysokość i kąty uformowane w wierzchołkach. Aby określić obszar w tych przypadkach, konieczne jest zastosowanie przyczyn trygonometrycznych.
Znając kąt jednego z jego wierzchołków, kategoria jest zidentyfikowana i stosuje się odpowiedni rozum trygonometryczny:
 Wzór trygonometryczny do obliczenia boków trójkąta skalenicznego
Wzór trygonometryczny do obliczenia boków trójkąta skalenicznego Na przykład Cateto AB będzie odwrotnie dla kąta C, ale w sąsiedztwie kąta A. W zależności od boku lub nogi odpowiadającej wysokości, druga strona jest wyczyszczona, aby uzyskać wartość tego.
Rozwiązane ćwiczenia
Pierwsze ćwiczenie
Oblicz obszar i wysokość trójkąta Escalano ABC, wiedząc, że jego boki to:
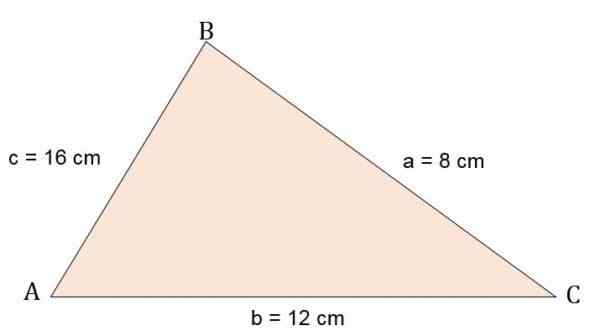
A = 8 cm.
B = 12 cm.
C = 16 cm.
Rozwiązanie
Ponieważ dane są podawane miary trzech stron trójkąta skalenicznego.
Ponieważ nie masz wartości wysokości, obszar można ustalić, stosując formułę Herón.
Najpierw obliczany jest pół -perymetr:
SP = (A + B + C) ÷ 2
SP = (8 cm + 12 cm + 16 cm) ÷ 2
SP = 36 cm ÷ 2
SP = 18 cm.
Teraz wartości w formule Heróna zostaną zastąpione:
Może ci służyć: Częstotliwość bezwzględna: wzór, obliczenia, rozkład, przykład Formuła Herón
Formuła Herón Znajomość obszaru można obliczyć względną wysokość na bok B. Z ogólnej formuły, oczyszczając go:
Obszar = (strona * H) ÷ 2
46, 47 cm2 = (12 cm * H) ÷ 2
H = (2 * 46,47 cm2) ÷ 12 cm
H = 92,94 cm2 ÷ 12 cm
H = 7,75 cm.
Drugie ćwiczenie
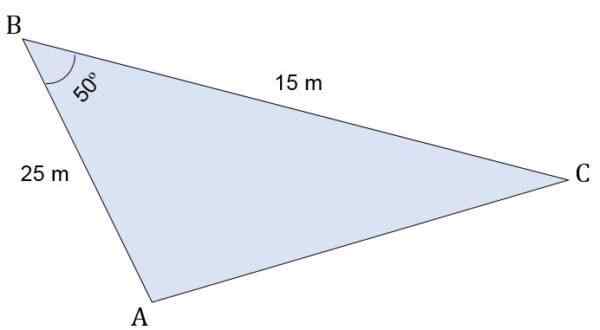
Biorąc pod uwagę trójkąt ABC Escalano, którego miary to:
- Segment AB = 25 m.
- Segment BC = 15 m.
W wierzchołku B powstaje kąt 50º. Oblicz wysokość w stosunku do boku C, obwodu i powierzchni tego trójkąta.
Rozwiązanie
W takim przypadku istnieją dwie środki. Aby określić wysokość, konieczne jest obliczenie miary trzeciej strony.
Ponieważ podane strony podane jest odwrotny kąt, możliwe jest zastosowanie prawa Cosenos w celu ustalenia miary strony AC (B):
B2 = a2 + C2 - 2*C * cos b
Gdzie:
A = BC = 15 m.
C = AB = 25 m.
B = AC.
B = 50albo.
Dane są zastąpione:
B2 = (15)2 + (25)2 - 2*(piętnaście)*(25) * cos 50
B2 = (225) + (625) - (750) * 0,6427
B2 = (225) + (625) - (482 025)
B2 = 367 985
B = √367,985
B = 19,18 m.
Ponieważ masz już wartość trzech stron, obliczany jest obwód tego trójkąta:
P = strona z boku + strona B +
P = 15 m + 25 m + 19, 18 m
P = 59,18 m
Teraz możliwe jest określenie obszaru poprzez zastosowanie formuły Herón, ale najpierw należy obliczyć pół -perymetr:
SP = P ÷ 2
SP = 59,18 m ÷ 2
SP = 29,59 m.
Miary boków i półprzewód w formule Heróna są zastąpione:

Wreszcie, znając obszar, wysokość względną można obliczyć na bok C. Z ogólnej formuły, oczyszczając go, musisz:
Obszar = (strona * H) ÷ 2
143,63 m2 = (25 m * H) ÷ 2
H = (2 * 143,63 m2) ÷ 25 m
H = 287,3 m2 ÷ 25 m
H = 11,5 m.
Trzecie ćwiczenie
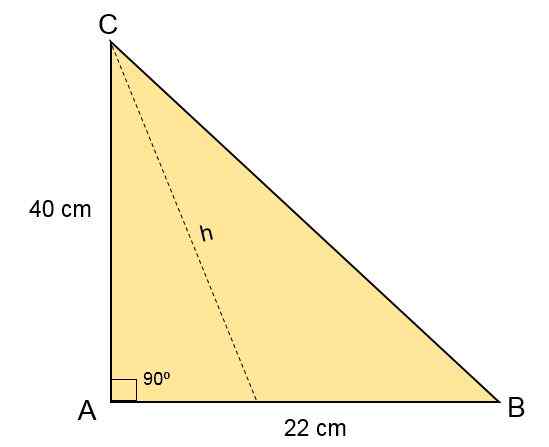
W trójkącie Escaleno ABC strona B mierzy 40 cm, strona C mierzy 22 cm, a w wierzchołku A jest kątem 90albo. Oblicz obszar tego trójkąta.
Rozwiązanie
W tym przypadku podane są miary dwóch stron trójkąta skali ABC, a także kąt utworzony w wierzchołku do.
Aby określić obszar, nie jest konieczne obliczenie miary strony A, ponieważ poprzez przyczyny trygonometryczne kąt służy do jego znalezienia.
Ponieważ przeciwny kąt jest znany wysokości, zostanie to określone przez produkt z jednej strony i piersi kąta.
Zastępując w formule obszaru, musisz:
- Obszar = (strona * H) ÷ 2
- H = c * Sin a
Obszar = (b * C * sin a) ÷ 2
Obszar = (40 cm * 22 cm * Sen 90) ÷ 2
Obszar = (40 cm * 22 cm * 1) ÷ 2
Obszar = 880 cm2 ÷ 2
Obszar = 440 cm2.
Bibliografia
- Álvaro rendón, do. R. (2004). Rysunek techniczny: Notatnik aktywności.
- Ángel Ruiz, H. B. (2006). Geometrie. CR technologia, .
- Anioł, a. R. (2007). Algebra podstawowa. Edukacja Pearsona,.
- Baldor, a. (1941). Algebra. Hawana: Kultura.
- Barbosa, J. L. (2006). Płaska geometria euklidesowa. Rio de Janeiro,.
- Coxeter, godz. (1971). Podstawy geometrii. Meksyk: Limusa-Wiley.
- Daniel c. Alexander, g. M. (2014). Podstawowa geometria dla studentów. Cengage Learning.
- Harpe, str. D. (2000). Tematy w teorii grupy geometrycznej. University of Chicago Press.

