Tidecágono

Rysunek 1.- Po lewej stronie regularny Tridecácágone i po prawej walucie 20 koron Republiki Czeskiej, z konturem w kształcie ślubnej w kształcie ślubu wpisanego w obwód, z jednej strony ma lew bohemii Republiki Czeskiej, zamontowanej na koniu. Źródło: f. Zapata.

Co to jest Tridecágono?

TrideCagon to płaska geometryczna postać rodziny wielokątów i charakteryzuje się ma 13 stron i 13 wierzchołków. Inna nazwa tego wielokąta to Tradaidecágono, Liczba pochodząca z greckiego.

13 stron to segmenty linii, które w końcu zbliżają się do kształtowania figury. Wielokąty, które są nazwane według liczby stron, są bogatym źródłem inspiracji dla architektury, konstrukcji i projektowania wielu przedmiotów, zarówno sztuki, jak i utylitarów.

Właściwości Tridecágono

Tridecágono dzieli z innymi wielokątami następującymi cechami i właściwościami:

-boki, Są to segmenty linii, które są połączone, tworząc figurę, która w przypadku Tridecágono wynosi 13. Są one identyfikowane przez małe litery.

-Wierzchołki, Tak nazywane są punkty przecięcia kolejnych stron i zwykle oznaczają litery kapitałowe. Tridecágono ma 13 wierzchołków.

-Obwód, równoważny sumę boków. Jeśli wszystkie strony mają równą miarę „a”, obwód wynosi po prostu 13 × a, ale jeśli boki są nierówne, wówczas obwód dodaje każdą z długości boków.

-Centrum, Jest to punkt, który utrzymuje tę samą odległość zarówno z wierzchołkami, jak i bokami.

-Przekątna, Linia, która dołącza do wierzchołka z innym nie -konsekwentnym wierzchołkiem (kolejne wierzchołki są zjednoczone z bokami).

-Kąty wewnętrzne, Powstają między dwiema sąsiednimi stronami figury i na wewnętrznej części wielokąta, a jej wierzchołek jest wspólnym wierzchołkiem po obu stronach.

Może ci służyć: Miletus taki twierdzenie

-Kąty zewnętrzne, Są poza wielokątem, między jedną stroną a przedłużeniem jednej z kolejnych stron.

-Radio, Odległość odległości Tridecágon.

-Kąt centralny, To ten, którego wierzchołek jest środkiem wielokąta.

-Apothem, segment, który dołącza do środka jednej strony ze środkiem figury i tworzą 90º z tą stroną.

Regularny i nieregularny grzmot

Threekarony mogą być:

-Regularny, Gdy miara wszystkich jego trzynastu stron jest taka sama, a jej wewnętrzne kąty mierzą to samo.

-Nieregularny, Jeśli jedna lub więcej stron ma różne miary.

W przypadku zwykłego Tridecácágone można zastosować następujące wzory:

Kąt wewnętrzny

W przypadku zwykłego wielokąta formuła, która pozwala obliczyć wartość kąta wewnętrznego, wynosi:

Gdzie n reprezentuje liczbę stron, które w tym przypadku wynosi 13. Z tą wartością jest to:

I = (11 × 180º)/13 ≈ 152.3

Piagonals

Liczba przekątnej jest obliczana na podstawie następującego wzoru, nawet poprawny, jeśli wielokąt jest nieregularny:

Dla n = 13 wyników:

D = 13 × 10/2 = 65 przekątnych

Apothem

Wartość Apothem l_DO  Oblicza się go z następującym formułem, będąc „długością strony:

L_DO ≅ 2.0286a

Obszar

Jeśli obwód P i długość apothem l_DO, Obszar Tridecágono oblicza się przez:

A = (P × L_DO)/2

W zależności od strony „A” formuła pozostaje:

A = (13a × l_DO)/2

Zastępując miarę_DO Z poprzedniej sekcji uzyskuje się formułę dla obszaru, który zależy tylko od długości strony:

A = (13a × 2.0286a)/2 ≈ 13.186a²

Może ci służyć: rozkład hipergeometryczny: wzory, równania, model

Ćwiczenia

Jeśli średnica koron 20 mm wynosi 26 mm, ile są strona i obszar Tridecágono zarejestrowany w kręgu waluty?

Rozwiązanie

Z postaci jest trójkąt prostokąta, którego kategorie są apotem i połowa długości boku, z hipotenusą równą promieniu waluty, która jest połową średnicy. Ponieważ jest to warte 26 mm, Radio R jest równe 13 mm.

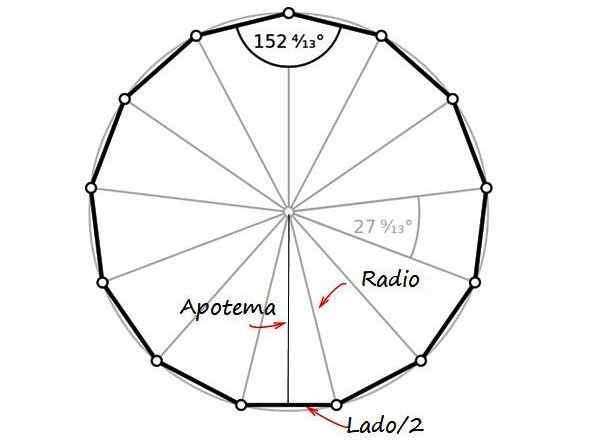Rysunek 2. Radio, apoteme i połowa boku trindecagon tworzą trójkąt prostokąta. Źródło: Wikimedia Commons/F. Zapata.

Autor: PiThagoras Twierdzenie:

Od L_DO ≈ 2.0286a, masz:

R² = (2.0286a)² + (0.5)² = 4.3652a²

Strona to:

Z tą wartością obszar waluty to:

A ≈ 13.186a² = 13.186 (6.222 mm)² = 510.5 mm²

Czytelnik pozostaje w celu porównania tego wyniku z obszarem uzyskanym przez zakładanie, że waluta jest okólna o promieniu r = 13 mm.

Jak tam Tridecágono?

Regularny trindecagon jest z wielokątów, który nie przyznaje dokładnej konstrukcji przy użyciu tylko reguły i kompasu, to znaczy nie jest to wielokąt, który można zbudować. Można je tylko zbudować, przynajmniej teoretycznie, te wielokąty, których liczba stron obejmuje tylko podstawowe czynniki formy:

W ten sposób nazywane są liczby pierwszorzędne Fermat kuzyni, Ale liczba 13, chociaż jest kuzynem, nie ma tej formy.

Jednak możesz narysować zwykły trindecagon, który jest zarejestrowany w obwodzie, każdy wierzchołek ma z nim skrzyżowanie, bez zauważania w nagim oku. W tym celu jest to konieczne.

Może ci służyć: Trójkąt Otusangle

Jednym ze sposobów na zbudowanie zwykłego Tridecácágone, choć nie jedyny, jest rysowanie pociągnięć, jak pokazano w następującej animacji:

Rysunek 3. Budowa zwykłego TrideCagon. Źródło: Wikimedia Commons.

I ta druga animacja opisuje także, jak zrobić Tridecágono w przybliżeniu, z regułą i kompasem:

Rysunek 4.- Alternatywny sposób na zbudowanie w przybliżeniu regularnego TrideCagon z regułą i kompasem. Źródło: Wikimedia Commons.

Przykłady Tridecágel

Wklęsły i wypukły grzmot

Gdy wewnętrzne kąty Tridecágono są mniejsze niż 180º, liczba jest wypukła, podczas gdy jeden lub więcej kątów wewnętrznych jest większe niż 180º, wówczas Tridecágono jest wklęsłe.

Zwykły Tridecácágon jest wypukły, ponieważ jego wewnętrzne kąty mierzą około 152.Trzeci każdy.

Zastosowanie Tridecágono w numizmatyce

Czeska korona

Numismatyka to nauka monet, medali, biletów i żetonów. Wielokąty po wielu stronach są idealne jako elementy dekoracyjne w projektowaniu monet, szczególnie te, które mają wiele stron, takich jak Tridecágono.

Jednak nie wszystkie monety są okrągłe, wielokąty po wielu stronach przypominają okrągły kształt, tym więcej ma strony, tym większe podejście. Dlatego projektanci monet używają wielokątów po wielu stronach, aby wprowadzić odrobinę oryginalności w swoim projekcie.

W tym celu stosuje się różne wielokąty, takie jak górna waluta, zwana koroną i z Czech, dobry przykład użycia Tridecágono jako elementu projektowego.

Bibliografia

1. Alexander, zm. 2013. Geometria. 5. Wydanie. Cengage Learning.
2. Rysunek. Zwykłe wielokąty. Odzyskane z: rysunek.com.
3. Hartley, m. Konstruowanie TrideCagon. Odzyskane z: YouTube.com
4. Wikipedia. Buildible Polygon. Odzyskane z: jest.Wikipedia.org.
5. Wikiwand. Tidecagon. Odzyskane z: Wikiwand.com.