Prostokątne właściwości, relacje i formuły, przykłady

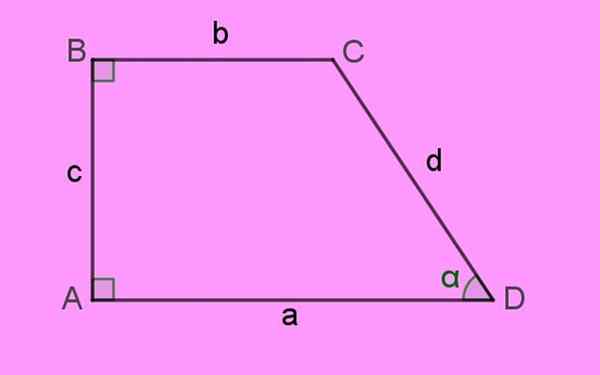
A Prostokąt trapezu Jest to płaska postać czterech stron, tak że dwie z nich są do siebie równoległe, zwane bazy A także jedna z pozostałych stron jest prostopadła do podstaw.

Z tego powodu dwa wewnętrzne kąty są proste, to znaczy mierzą 90º. Stąd nazwa „prostokąt”, która jest podana na figurę. Poniższy obraz prostokąta trapezu wyjaśnia te cechy:

[TOC]

Elementy trapezu

Elementy trapezu to:

-Bazy

-Wierzchołki

-Wysokość

-Kąty wewnętrzne

-Średnia baza

-Piagonals

Opiszemy te elementy za pomocą rysunków 1 i 2:

Rysunek 1. Prostokątny trapez, charakteryzujący się dwoma wewnętrznymi kątami 90º: A i B. Źródło: f. Zapata.

Boki prostokąta trapezu są oznaczone małymi literami A, B, C i D. Zakątki figury lub Wierzchołki Są one wskazane literami kapitałowymi. Wreszcie Kąty wewnętrzne Są wyrażane greckim literami.

Zgodnie z definicją, bazy Tego trapezu to boki a i b, które zaobserwowane są równoległe, a także mają różną długość.

Strona prostopadła do obu podstaw jest bokiem C po lewej stronie, czyli wysokość H trapezu. I wreszcie istnieje strona D, która tworzy ostry kąt α z bokiem A.

Suma Kąty wewnętrzne czworoboków wynosi 360º. Łatwo doceniane jest, że brakujący kąt C na rysunku wynosi 180 - α.

średnia baza Jest to segment, który łączy się z środkami nierównoległymi stronami (segment EF na ryc. 2).

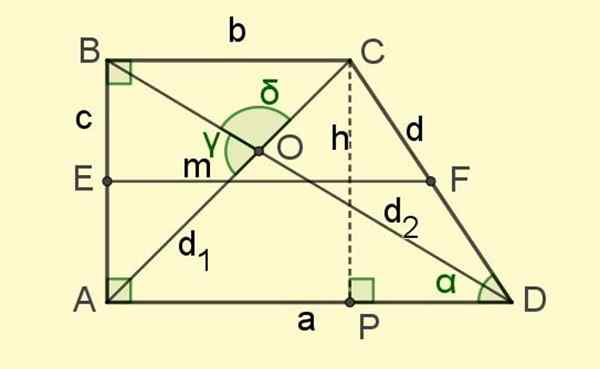Rysunek 2. Elementy prostokąta trapezu. Źródło: f. Zapata.

I wreszcie są przekąski d₁ i d₂, segmenty, które łączą przeciwne wierzchołki i przecinają się w punkcie O (patrz ryc. 2).

Relacje i formuły

Wysokość H trapezu

H = c

Obwód p

Jest to miara konturu i jest obliczana przez dodanie boków:

Obwód = A + B + C + D

Strona D Jest wyrażany w kategoriach wysokości lub strony C Przez twierdzenie Pitagorasa:

D = √ (A-B)² + C²

Zastąpienie na obwodzie:

P = a + b + c + √ (a-b)² + C²

Średnia baza

To pół -bodie podstaw:

Średnia podstawa = (a+b)/2

Czasami znaleziono średnią bazę wyrażoną w ten sposób:

Średnia podstawa = (główna podstawa + mniejsza baza) /2

Obszar

Obszar A trapezu jest produktem średniej bazy według wysokości:

A = (Główna podstawa + mniejsza baza) x wysokość /2

A = (a+b) c/2

Przekątne, boki i kąty

Kilka trójkątów pojawia się na ryc. 2, zarówno prostokąty, jak i nierelektywne. Do tych, którzy mają właściwe trójkąty, mogą być stosowane przez twierdzenie Pitagorasa i tych, którzy tego nie robią, twierdzenia o cosinusie i piersi.

Może ci służyć: liczby transcendentne: co to są, formuły, przykłady, ćwiczenia

W ten sposób istnieją relacje między bokami i między bokami i wewnętrznymi kątami trapezo.

Trójkąt CPA

Jest to prostokąt, jego nogi są takie same i są warte b, a przeciwprostokąt₁, W związku z tym:

D₁² = b² + B² = 2b²

Trójkąt DAB

Jest to również prostokąt, nogi są Do I C (lub także Do I H), A przeciwprostanie to d₂, aby:

D₂² = a² + C² = a² + H²

Trójkąt CDA

Ponieważ ten trójkąt nie jest prostokątem, zastosowano twierdzenie cosinusowe lub piersi.

Według twierdzenia Coseno:

D₁² = a² + D² - 2AD cos α

Trójkąt CDP

Ten trójkąt jest prostokątem, a z bokami zbudowano trygonometryczne przyczyny kąta α:

sin α = h/d

COS α = PD/D

Ale strona PD = A - B, dlatego:

cos α = (a -b) / d → a - b = d cos α

a = b + d cos α

Masz także:

Tg α = sin α / cos α = h / (a-b) → h = tg α (a-b)

Trójkąt CDB

W tym trójkącie mamy kąt, którego wierzchołek jest w C. Nie jest oznaczony na figurze, ale na początku wyróżniał się, że jest wart 180 - α. Ten trójkąt nie jest prostokątem, więc twierdzenie cosinusa lub twierdzenie o piersi można zastosować.

Teraz można łatwo wykazać, że:

Sen (180 - α) = sin α

cos (180 - α) = - cos α

Stosowanie twierdzenia Coseno:

D₂² = d² + B² - 2db cos (180 - α) = D² + B² + 2DB cos α

Przykłady prostokątów

Trapezy, a zwłaszcza prostokąty znajdują się po wielu stronach, a czasem nie zawsze namacalne. Tutaj mamy kilka przykładów:

Trapecio jako element projektowy

W architekturze licznych budynków, takich jak ten kościół w Nowym Jorku, obfitują w architekturę geometryczne, które pokazują strukturę w postaci prostokątnej trapezu.

Również forma trapezoidalna jest częsta w projektowaniu pojemników, pojemników, ostrzy (Nóż lub dokładne), arkusze i w projektowaniu graficznym.

Rysunek 3. Anioł wewnątrz prostokąta trapez w kościele w Nowym Jorku. Źródło: David Goehring przez Flickr.

Trapezoidalny generator fali

Sygnały elektryczne mogą być nie tylko kwadratowe, sinusoidalne lub trójkątne. Istnieją również sygnały trapezoidalne, które są przydatne w wielu obwodach. Na rycinie 4 znajduje się sygnał trapezoidalny złożony z dwóch prostokątów. Między nimi tworzą pojedynczy trapeza izosceles.

Może ci służyć: dzielnicy 8: co to jest i łatwe wyjaśnienie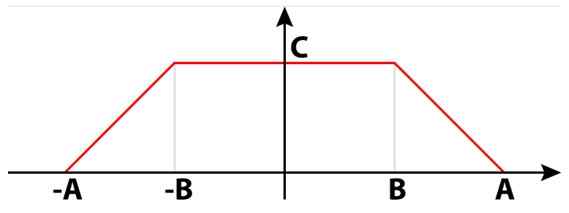Rysunek 4. Sygnał trapezoidalny. Źródło: Wikimedia Commons.

W obliczeniach numerycznych

Aby obliczyć numerycznie zdefiniowaną całkę funkcji f (x) między a i b, reguła trapezu służy do przybliżenia obszaru pod wykresem f (x). Na poniższym rysunku, po lewej stronie zintegrowani podejście z pojedynczym prostokątnym trapezem.

Lepszym podejściem jest właściwa figura, z wieloma prostokątami.

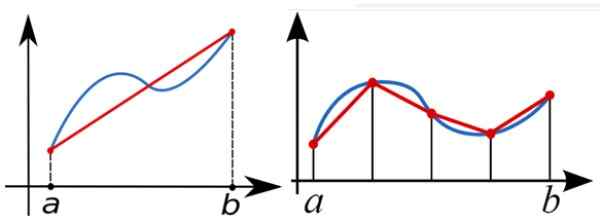Rysunek 5. Zdefiniowana całka między A i B jest niczym innym jak obszarem pod krzywą F (x) między tymi wartościami. Prostokątne trapezoid może służyć jako pierwsze podejście do tego obszaru, ale im więcej trapezów jest używane, tym lepsze podejście. Źródło: Wikimedia Commons.

Trapezoidalna wiązka obciążenia

Siły nie zawsze koncentrują się na jednym punkcie, ponieważ ciała, na których działają, mają znaczące wymiary. Tak jest w przypadku mostu, przez który pojazdy ciągle krążą, woda basenu na pionowych ścianach tego samego lub dachu, na którym gromadzi się woda lub śnieg.

Dlatego siły są rozmieszczone na jednostkę długości, powierzchni lub objętości, w zależności od ciała, na którym działają.

W przypadku wiązki siła rozmieszczona na jednostkę długości może mieć różne rozkłady, na przykład w prostokątnym trapezie pokazanym poniżej:

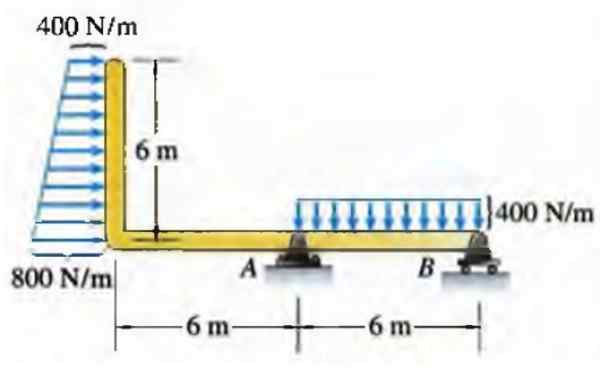Rysunek 6. Ładuje wiązkę. Źródło: Bedford, do. 1996. Statyczny. Addison Wesley Inter -American.

W rzeczywistości nie zawsze rozkłady odpowiadają regularnym formom geometrycznym, takim jak to, ale w wielu przypadkach mogą być dobrym podejściem.

Jako narzędzie edukacyjne i uczenia się

Bloki i arkusze o geometrycznych kształtach, w tym trapezoidy, są bardzo przydatne dla dzieci do zapoznania się z najmłodszych lat z fascynującym światem geometrii.

Rysunek 7. Bloki z prostymi geometrycznymi kształtami. Ile prostokątów jest ukrytych w blokach? Źródło: Wikimedia Commons.

Rozwiązane ćwiczenia

- Ćwiczenie 1

W prostokąta trapez na rycinie 1 największa podstawa jest warta 50 cm, a najmniejsza podstawa jest równa 30 cm, wiadomo również, że skośna strona mierzy 35 cm. Znajdować:

a) kąt α

b) Wysokość

c) obwód

d) średnia baza

e) obszar

f) przekątne

Rozwiązanie

Dane instrukcji są podsumowane w ten sposób:

A = wyższa podstawa = 50 cm

B = mniejsza baza = 30 cm

D = pochylona strona = 35 cm

Może ci służyć: podstawowe operacje

Aby znaleźć kąt α, odwiedzamy sekcję formuły i równań, aby zobaczyć, który najlepiej pasuje do oferowanych danych. Poszukiwany kąt znajduje się w kilku analizowanych trójkątach, na przykład CDP.

Tam mamy tę formułę, która zawiera nieznane, a także dane, które znamy:

cos α = (a-b) / d

Dlatego:

α = łuki [(A-B) / D] = łuki [(50-30) / 35] = łuki 20/35 = 55.15 °

Rozwiązanie b

Z równania:

sin α = h/d

H:

H = D.sin α = 35 Sen 55.15 ° CM = 28.72 cm

Rozwiązanie c

Obwód jest sumą boków, a ponieważ wysokość jest równa strony C, musimy:

C = H = 28.72 cm

Dlatego:

P = (50 + 30 + 35 + 28.72) cm = 143.72 cm

Rozwiązanie d

Średnia baza to półprodukty baz:

Średnia podstawa = (50 + 30 cm)/2 = 40 cm

Rozwiązanie e

Obszar trapezu to:

A = średnia podstawa x wysokość = 40 cm x 28.72 = 1148.8 cm².

Rozwiązanie f

Dla Diagonal D₁ Tę formułę można użyć:

D₁² = b² + B² = 2b²

D₁²= 2 x (30 cm)² = 1800 cm²

D₁ = √1800 cm² = 42.42 cm

I dla przekątnej d₂:

D₂² = d² + B² + 2DB cos α = (35 cm)² + (30 cm)² + 2 x 35 x 30 cm² Cos 55.15 ° = 3325 cm²

D₂ = √ 3325 cm² = 57.66 cm

To nie jest jedyny sposób na znalezienie d₂, Ponieważ jest też trójkąt DAB.

- Ćwiczenie 2

Następujący wykres prędkości w zależności od telefonu komórkowego, który ma jednolicie przyspieszony ruch prostoliniowy. Oblicz odległość przebywającą przez telefon komórkowy w przedziale czasowym między 0.5 i 1.2 sekundy.

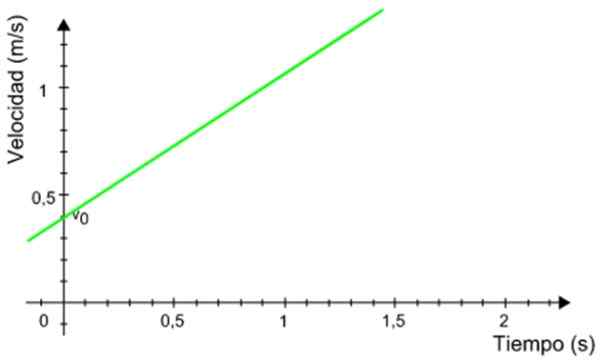Cyfra 8. Grafika z czasem telefonu komórkowego z jednolicie przyspieszonym ruchem Reknet. Źródło: Wikimedia Commons.

Rozwiązanie

Odległość przebywająca przez telefon komórkowy jest równoważny obszarowi pod wykres.

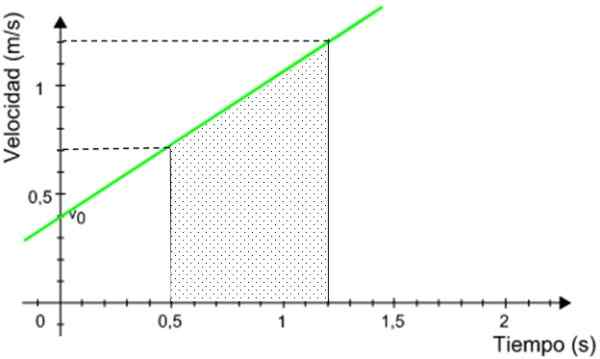Rysunek 9. Odległość przebywająca przez telefon komórkowy jest równoważny obszarowi pod grafiką. Źródło: Zmodyfikowane przez F. Zapata.

Zacieniony obszar to obszar prostokąta trapezu, podany przez:

A = (Główna podstawa + mniejsza baza) x wysokość /2

A = (1.2 + 0.7) m/s x (1.20.5) S/2 = 0.665 m

Bibliografia

1. Baldor, a. 2004. Płaska i przestrzeń geometria z trygonometrią. Publikacje kulturalne.
2. Bedford, a. 1996. Statyczny. Addison Wesley Inter -American.
3. Jr. Geometria. 2014. Wielokąty. Lulu Press, Inc.
4. Onlinemschool. Prostokąt trapezu. Odzyskane z: jest.Onlinemschool.com.
5. Automatyczna geometria rozwiązywania problemów. Trapez. Odzyskane z: scuolaetrica.Przedmiot
6. Wikipedia. Trapecio (geometria). Odzyskane z: jest.Wikipedia.org.