Trapecio Isosceles Właściwości, relacje i wzory, przykłady

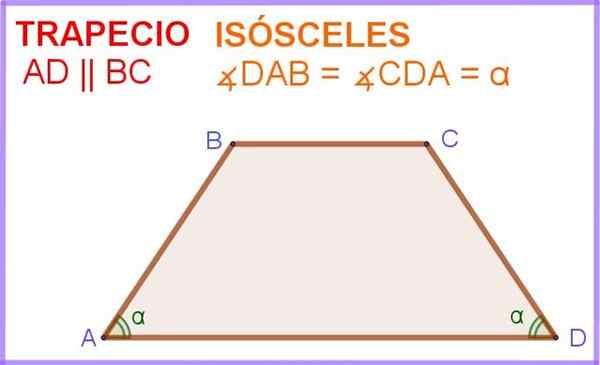
A trapez równoramienny Jest czworobokiem, w którym dwie strony są równoległe do siebie, a także dwa kąty przylegające do jednej z tych równoległych stron mają tę samą miarę.

Na rycinie 1 masz czworobok ABCD, w którym strony AD i BC są równoległe. Dodatkowo kąty ∠DAB i ∠ADC sąsiadujące z równoległym bocznym AD mają tę samą miarę α. 

Rysunek 1. Izosceli trapez. Źródło: f. Zapata.

Zatem ten czworoboczny lub czteroosobowy wielokąt jest w efekcie trapeza izosceles.

W trapezie nazywane są równoległe strony bazy i nazywane są nie-paralle boczny. Kolejną ważną cechą jest wysokość, czyli odległość oddzielająca boki równoległe.

Oprócz trapezu Isosceles istnieją inne rodzaje trapezu:

-TRapecio Escaleno, który ma różne swoje kąty i strony.

-TRectangle Rapecio, w którym strona ma proste sąsiednie kąty.

Forma trapezoidalna jest częsta w różnych obszarach projektowania, architektury, elektroniki, obliczeń i wielu innych, jak to będzie widać później. Stąd znaczenie zapoznania się z jego właściwościami.

[TOC]

Nieruchomości

Ekskluzywny trapezd Isosceles

Jeśli trapez to izosceles, spełnia następujące charakterystyczne właściwości:

1.- Boki mają tę samą miarę.

2.- Kąty sąsiadujące z bazami są takie same.

3.- Przeciwne kąty są uzupełniające.

4.- Piagonals mają tę samą długość, to samo to dwa segmenty, które łączą przeciwne wierzchołki.

5.- Kąt utworzony między zasadami i przekątnymi są tego samego miary.

6.- Ma ograniczony obwód.

Wzajemnie, jeśli trapez spełnia którąkolwiek z poprzednich właściwości, to jest to trapeza izosceles.

Jeśli w izosceli trapezowych jednym z kąta jest proste (90º), to wszystkie inne kąty będą również tworząc prostokąt. To znaczy prostokąt jest szczególnym przypadkiem trapezu izosceles.

Rysunek 2. Pojemnik i stoły szkolne kukurydzy mają kształt izosceli. Źródło: pxfuel (po lewej)/McDowell Craig przez Flickr. (Prawidłowy)

Dla wszystkich trapezoidów

Poniższy zestaw właściwości jest ważny dla każdego trapezu:

7.- mediana trapezu, to jest segment, który łączy punkty środkowe jego nierównoległych stron, jest równolegle do dowolnej podstawy.

8.- Długość mediany jest równa półsemum (suma podzielona przez 2) długości jej podstaw.

9.- Mediana trapezu przecina swoje przekąsy w punkcie środkowym.

10.- Pokrzycie trapez przecinają się w punkcie, który dzieli je na dwie sekcje proporcjonalne do ilorazów podstaw.

jedenaście.- Suma kwadratów przekątnych trapezu jest równa suma kwadratów jego boków oraz podwójny produkt jego podstaw.

Może ci służyć: ile tysięcznych mieszczą się w ciągu jednej dziesiątej?

12.- Segment, który dołącza do punktów środkowych, ma długość równą półprzezroczce podstaw.

13.- Kąty przylegające do boków są uzupełniające.

14.- Trapez ma zarejestrowany obwód, jeśli i tylko wtedy, gdy suma jego podstaw jest równa suma jego boków.

piętnaście.- Jeśli trapez ma zarejestrowany obwód, to kąty z wierzchołkiem pośrodku wspomnianego obwodu i boków przechodzących przez końce tej samej strony są prostymi kątami.

Relacje i formuły

Poniższy zestaw relacji i wzorów jest określany do ryc. 3, gdzie oprócz izosceles trapezowych innych ważnych segmentów, takich jak przekątne, wysokość i średnie.

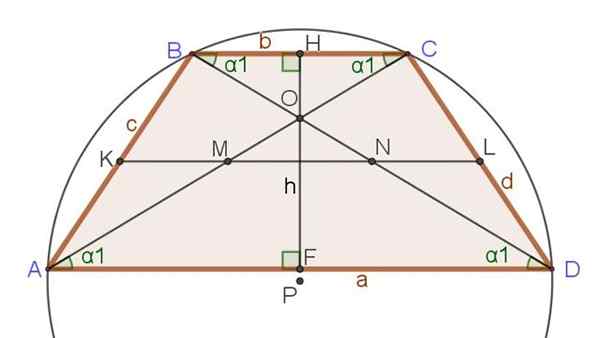Rysunek 3. Mediana, przekątna, wysokość i obwód ograniczone w trapezie izosceles. Źródło: f. Zapata.

Wyłączne relacje izosceles Trapecio

1.- AB = DC = C = D

2.- ∡Dab = ∡cda i ∡Abc = ∡bcd

3.- ∡Dab + ∡bcd = 180º i ∡CDA + ∡ABC = 180º

4.- BD = AC

5.- ∡cad = ∡bda = ∡cbd = ∡bca = α₁

6.- A, b, c i d należą do ograniczonego obwodu.

Relacje dla każdego trapezu

7. Jeśli AK = KB i DL = LC ⇒ KL || AD i KL || pne

8.- Kl = (AD + BC)/2

9.- AM = MC = AC/2 i DN = NB = DB/2

10.- AO/OC = AD/BC Y DO/OB = AD/BC

jedenaście.- AC² + Db² = Ab² + DC² + 2⋅AD⋅BC

12.- Mn = (AD - BC)/2

13.- ∡Dab + ∡Abc = 180º i ∡cda + ∡bcd = 180º

14.- Jeśli AD + BC = AB + DC ⇒ ∃ R What Equidista AD, BC, AB i DC

piętnaście.- Jeśli ∃ r, co równoodgórze AD, BC, AB i DC, to:

∡Bra = ∡drc = 90º

Isosceles relacje trapezoidalne z zarejestrowanym obwodem

Jeśli w trapezie izosceles suma zasad jest równa podwójnej stronie, wówczas istnieje zarejestrowany obwód.

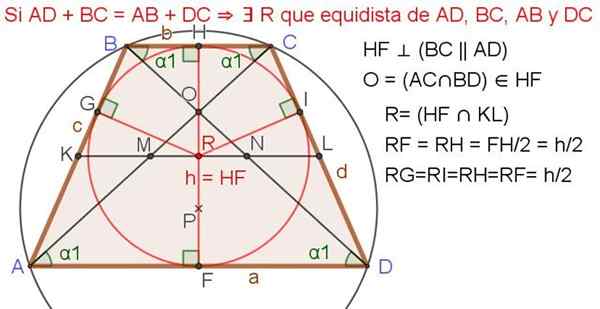Rysunek 4. Trapez z zarejestrowanym obwodem. Źródło: f. Zapata.

Następujące właściwości obowiązują, gdy trapeza Isosceles ma zarejestrowany obwód (patrz rysunek 4 powyżej):

16.- KL = AB = DC = (AD + BC)/2

17.- Piagonale są wycinane pod kątem prostym: ac ⊥ bd

18.- Wysokość jest taka sama jak mediana: hf = kl, czyli h = m.

19.- Kwadrat wysokości jest równy iloczynowi podstaw: H² = BC⋅AD

20.- W tych konkretnych warunkach obszar trapezu jest równy kwadratowi wysokości lub produktu podstaw: obszar = h² = BC⋅AD.

Wzory do określenia jednej strony, znane pozostałe i kąt

Znana jedna podstawa, bok i kąt, drugą podstawę można określić przez:

A = B + 2C cos α

B = A - 2C cos α

Jeśli długość zasad jest znana jako znana i kąt, długości obu stron wynosi:

Może ci służyć: limit fermat: to, co składa się i ćwiczenia rozwiązane

C = (A - B) / (2 cos α)

Determinacja z jednej strony, znana pozostałe i przekątna

A = (d₁² - C²)/ B;

B = (D₁² - C²)/ Do 

C = √ (d₁² - A⋅B)

Gdzie d₁ Jest to długość przekątnych.

Podstawa od wysokości, obszaru i drugiej bazy

a = (2 a)/h - b

B = (2 a)/h - a

Znane z tyłu baz, obszar i kąt

C = (2a) /[(a + b) sin α]

Znana boczna mediana, obszar i kąt

C = a / (m.sin α)

Znany wysokość boków

H = √ [4 c² - (A - B)²]

Znany wzrost kąt i dwie strony

H = TG α⋅ (A - B)/2 = C . sin α

Znane przekąski wszystkie strony lub dwie strony i kąt

D₁ = √ (c²+ A B)

D₁ = √ (a²+ C² - 2 A C cos α)

D₁ = √ (b² + C²- 2 b c cos β)

Isosceles Triangle Perimeter 

P = A + B + 2C

Izosceles obszar trapezoidalny

Istnieje kilka formuł do obliczenia obszaru, w zależności od znanych danych. Poniżej znajduje się najbardziej znany, w zależności od podstaw i wysokości:

A = H⋅ (A + B)/2

A te inne można również użyć:

-Jeśli boki są znane

A = [(a +b)/4] √ [4c² - (A - B)²]

-Kiedy masz dwie strony i kąt

A = (B + C cos α) C Sen α = (A - C cos α) C Sen α

-Jeśli promień zarejestrowanego obwodu jest znany i kąt

A = 4 r² / Sin α = 4 r² / Sin β

-Kiedy znane są podstawy i kąt

A = a⋅b / sin α = a⋅b / sen β 

-Jeśli trapez można zarejestrować obwód

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b)/2

-Znane po przekątnej i kątach, które tworzą się ze sobą

A = (d₁²/2) Sen γ = (D₁² / 2) Sen δ 

-Kiedy masz stronę, medianę i kąt

A = MC.sin α = MC.Sen β

Zrezygnowane radio o obwodzie

Tylko trapezoidy Isosceles mają ograniczony obwód. Jeśli główna podstawa jest znana, strona C i przekątna d₁, Następnie promień r obwodu, który przechodzi przez cztery wierzchołki trapezu, wynosi:

R = A⋅C⋅D₁ / 4√ [p (p -a) (p -c) (p -d₁)]

Gdzie p = (a + c + d₁) / 2

Przykłady zastosowania trapezu Isosceles

Trapezoid Isosceles pojawia się w dziedzinie projektowania, jak pokazano na rycinie 2. I tutaj mamy kilka dodatkowych przykładów:

W architekturze i budownictwie

Starożytne Inkowie znały izosceles trapezoid i użył go jako elementu konstrukcyjnego w tym oknie Cuzco, Peru:

Rysunek 5 . Okno o trapezoidalnej formie Coricancha, cuzco. Źródło: Wikimedia Commons.

I tutaj trapeza pojawia się ponownie w rozmowie Trapezoidalny arkusz, Często używany materiał w konstrukcji:

Rysunek 6. Trapezoidalny arkusz metalowy tymczasowo chroniąc okna budynku. Źródło: Wikimedia Commons.

W projektowaniu

Widzieliśmy już, że trapez Isosceles pojawia się w codziennych przedmiotach, w tym pokarmy, takie jak ten batonik czekoladowy:

Rysunek 7. Czekoladowy, którego twarze mają kształt izosceli. Źródło: pxfuel.

Rozwiązane ćwiczenia

- Ćwiczenie 1

Trapezoid Isosceles opiera się niż 9 cm, podstawa mniejsza niż 3 cm, a jego przekątna 8 cm każda. Oblicz:

Może ci służyć: ogólne równanie paraboli (przykłady i ćwiczenia)

na bok

b) Wysokość

c) obwód

d) ärea

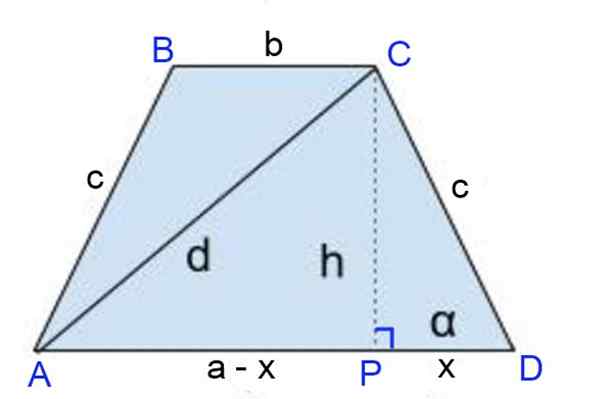Cyfra 8. Plan ćwiczenia 1. Źródło: f. Zapata

Rozwiązanie

Wysokość cp = h jest rysowana, gdzie stopa wysokości definiuje segmenty:

Pd = x = (a-b)/2 i 

Ap = a - x = a - a/2 + b/2 = (a + b)/2.

Przez twierdzenie Pitagorasa do trójkąta prostokąta DPC:

C² = h² + (A - B)² /4

A także do trójkąta prostokąta APC:

D² = h² + AP² = h² + (A+B)² /4

Wreszcie członek jest odejmowany, drugie równanie pierwszego i upraszcza:

D² - C² = ¼ [(A+B)² - (A-B)²] = ¼ [(a+b+a-b) (a+b-a+b)]

D² - C² = ¼ [2a 2b] = A B

C²= d² - A b ⇒ c = √ (d² - a b) = √ (8² - 9⋅3) = √37 = 6,08 cm

Rozwiązanie b

H² = d² - (A+B)² /4 = 8² - (12² / 2² ) = 8² - 6² = 28

H = 2 √7 = 5,29 cm

Rozwiązanie c

Obwód = A + B + 2 C = 9 + 3 + 2⋅6,083 = 24 166 cm

Rozwiązanie d

Obszar = h (a+b)/2 = 5,29 (12)/2 = 31,74 cm

- Ćwiczenie 2

Istnieje trapez z izosceles, którego największa podstawa jest dwukrotnie mniejsza, a jej najmniejsza podstawa jest równa wysokości, która wynosi 6 cm. Określić:

a) bok boku

b) Obwód

c) obszar

d) Kąty

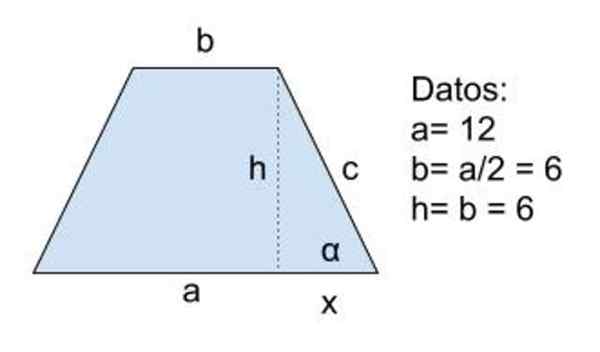Cyfra 8. Schemat ćwiczeń 2. Źródło: f. Zapata

Rozwiązanie

Dane: a = 12, b = a/2 = 6 i h = b = 6

Trzymamy się w ten sposób: wysokość H jest rysowana, a twierdzenie Pitagorasa jest stosowane do trójkąta hipotenu „C” i Catetos H i X:

C² = h²+XC²

Następnie musisz obliczyć wartość wysokości na podstawie danych (H = B) i Cateto X: 

a = b + 2 x ⇒ x = (a-b)/2

Zastępując poprzednie wyrażenia:

C² = b²+(A-B)²/2²

Teraz wartości numeryczne są wprowadzane i uproszczone:

C² = 62+ (12-6) 2/4

C² = 62 (1+¼) = 62 (5/4)

Uzyskanie:

C = 3√5 = 6,71 cm

Rozwiązanie b

Obwód p = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Rozwiązanie c

Obszar oparty na wysokości i długości podstaw to:

A = H⋅ (A + B)/2 = 6⋅ (12 + 6)/2 = 54 cm²

Rozwiązanie d

Kąt α, który tworzy bok z główną podstawą, jest uzyskiwana za pomocą trygonometrii:

Tan (α) = h / x = 6/3 = 2

α = arctan (2) = 63,44º

Drugi kąt, który tworzy stronę z niewielką zasadą, to β, który jest uzupełniający α:

β = 180º - α = 180º - 63,44º = 116,56º

Bibliografia

1. I. DO. 2003. Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
2. Campos, f. 2014. Matematyka 2. Grupa redakcyjna Patria.
3. Freed, k. 2007. Odkryj wielokąty. Benchmark Education Company.
4. Hendrik, v. 2013. Uogólnione wielokąty. Birkhäuser.
5. Iger. Matematyka pierwszy semestr Tacaná. Iger.
6. Jr. Geometria. 2014. Wielokąty. Lulu Press, Inc.
7. Miller, Heeren i Hornsby. 2006. Matematyka: rozumowanie i aplikacje. 10.  Wydanie. Edukacja Pearsona.
8. Patiño, m. 2006. Matematyka 5. Progreso redakcyjne.
9. Wikipedia. Trapez. Odzyskane z: jest.Wikipedia.com