Przykłady i równania Escaleno Trapezio, wzory i równania

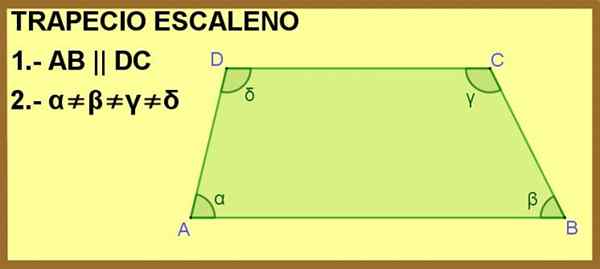
A trapez różnoboczny Jest to czterokątny wielokąt, z których dwa są równoległe do siebie, a z czterema kątami wewnętrznymi o różnych pomiarach.

Pokazany jest ABCD Quadrilateral, gdzie boki AB i DC są równoległe do siebie. Dzięki temu wystarczy, aby było to trapez, ale ponadto kąty wnętrza α, β, γ i δ są różne, dlatego trapezoid to escalano.

Rysunek 1. ABCD Quadrilateral jest trapezem dla warunku 1 i skalen dla warunku 2. Źródło: f. Zapata.

[TOC]

Elementy pułapki Scaleno

Poniżej najbardziej charakterystycznych elementów:

-Bazy i strona: Równoległe strony trapezu to jego podstawy, a dwie nierównoległe strony są bokami.

W trapezie skalene zasady są o różnych długościach, a boki. Jednak trapez saliny może mieć stronę o równej długości jak podstawa.

-Mediana: To segment łączy punkty środkowe boków.

-Przekątna: Poklęta trapezu to segment, który łączy dwa przeciwne wierzchołki. Trapez, jak każdy czworobok, ma dwie przekątne. W trapezie skalenicznym są one o różnej długości.

Inne trapezoidy

Oprócz Escaleno Trapezio istnieją inne szczególne trapezdy: trapezy prostokąta i trapeza izosceles.

Trapez jest prostokątem, gdy jeden z jego kątów jest prosty, podczas gdy Trapezio Isosceles ma swoje boki o równej długości.

Forma trapezoidalna ma wiele aplikacji na poziomie projektowania i branży, na przykład w konfiguracji skrzydeł samolotów, kształt codziennych obiektów, takich jak tabele, kopie zapasowe krzeseł, kontenery, portfele, druki tekstylne i wiele innych.

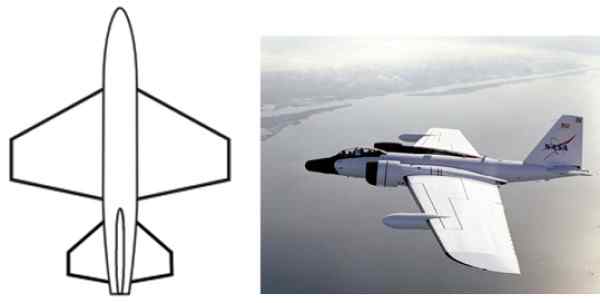Rysunek 2. Forma trapezoidalna jest powszechna w konfiguracji samolotu Alar. Źródło: Wikimedia Commons.

Nieruchomości

Następnie wymieniono właściwości trapezu wspinaczkowego, z których wiele jest obszernych dla innych rodzajów trapezu. W dalszej części, kiedy mówisz o „Trapezio”, nieruchomość będzie miała zastosowanie do każdego rodzaju, w tym skalen.

1. Mediana trapezu, to znaczy segment, który łączy środkowe punkty jego nierównoległych stron, jest równoległa do którejkolwiek z podstaw.

2.- Mediana trapezu ma długość, która jest półsoumem jego podstaw i przecina przekątną w punkcie środkowym.

3.- Przekąski trapez przecinają się w punkcie, które dzielą je na dwie sekcje proporcjonalne do stosunku podstaw.

4.- Suma kwadratów przekątnych trapezu jest równa suma kwadratów jego boków oraz podwójny produkt jego podstaw.

5.- Segment, który dołącza do punktów środkowych, ma długość równą półprzezroczce podstaw.

Może ci służyć: funkcja iniekcyjna: z czego składa się, do czego jest i przykłady

6.- Kąty przylegające do boków są uzupełniające.

7.- W trapezie skalenicznym długość jego przekątnej jest inna.

8.- Trapez ma zarejestrowany obwód tylko wtedy, gdy suma jego zasad jest równa suma jego boków.

9.- Jeśli trapez ma zarejestrowany obwód, to kąt z wierzchołkiem pośrodku wspomnianego obwodu i boków przechodzących przez końce bocznego trapezu jest prosty.

10.- Trapez Escaleno nie ma ograniczonego obwodu, jedynym rodzajem trapezu, że jeśli ma to Isosceles.

Wzory i równania

Następujące relacje trapezu wspinaczkowego są przekazywane do poniższej liczby.

1.- Jeśli AE = ED i BF = FC → EF || AB i EF || DC.

2.- Ef = (AB + DC)/2 to znaczy: m = (a + c)/2.

3.- Di = ib = d₁ /2 i ag = gc = d₂ /2.

4.- DJ / jb = (c / a) Podobnie CJ / ja = (c / a).

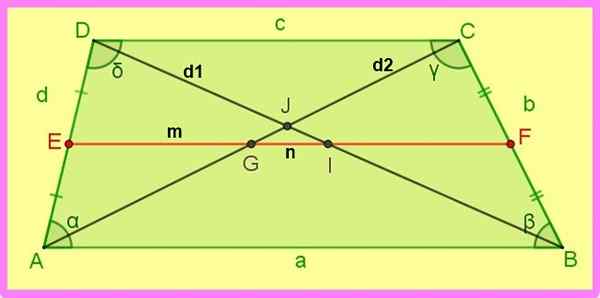Rysunek 3. Mediana i przekątna skalen trapezu. Źródło: f. Zapata.

5.- Db² + AC² = Ad² + pne² + 2 AB ∙ DC 

Równoważnie:

D₁² + D₂² = d² + B² + 2 a ∙ c

6.- GI = (AB - DC)/2

To jest do powiedzenia:

n = (a - c)/2

7.- α + δ = 180⁰ i β + γ = 180⁰

8.- Jeśli α ≠ β ≠ γ ≠ δ, to D1 ≠ D2.

9.- Rycina 4 pokazuje trapez skaleny, który ma zarejestrowany obwód, w takim przypadku spełniono, że:

A + C = D + B

10.- W trapezie escalenu ABCD z zarejestrowanym centrum centrum lub następujące jest również spełnione:

∡AOD = ∡BOC = 90⁰

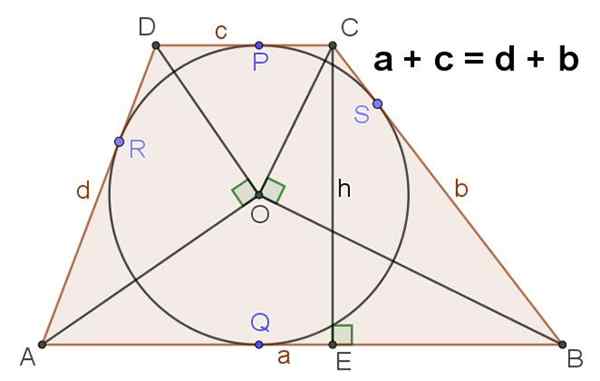Rysunek 4. Jeśli w trapezie sprawdza się, że suma jego zasad jest równa sumie boków, wówczas obwód jest napisany w tym samym. Źródło: f. Zapata.

Wysokość

Wysokość trapezu jest zdefiniowana jako segment, który przechodzi od punktu podstawy prostopadłowo do przeciwnej podstawy (lub jej rozszerzenia).

Wszystkie wysokości trapezu mają tę samą miarę H, więc przez większość czasu słowo wysokość odnosi się do jego pomiaru. Krótko mówiąc, wysokość jest odległością lub oddzieleniem podstaw.

Wysokość H można ustalić, czy znana jest długość strony i jeden z kąta przylegających do boku:

H = d sin (α) = d sin (γ) = b sin (β) = b sin (δ)

Mediana

Mediana miary M trapezoidów to półki podstawy:

M = (A + B)/2

Piagonals

D₁ = √ [a² + D² - 2 ∙ A ∙ D ∙ cos (α)]

D₂= √ [a² + B² - 2 ∙ A ∙ B ∙ cos (β)]

Można go również obliczyć, jeśli znana jest tylko długość trapezu:

D₁ = √ [b² + A ∙ c - a (b² - D²)/(a - c)]

D₂ = √ [d² + A ∙ c - a (d² - B²)/(a - c)]

Obwód

Obwód jest całkowitą długością konturu, to znaczy sumą wszystkich jego stron:

Może ci służyć: dyskretna zmienna losowa

P = a + b + c + d

Obszar

Obszar trapezoidów jest półproduktami jego podstaw pomnożonych przez jego wysokość:

A = h ∙ (a + b)/2

Można go również obliczyć, jeśli znana jest mediana M i wysokość:

A = m ∙ h

W przypadku, gdy znana jest tylko długość boków trapezowych, obszar może być określony przez formułę Heróna dla trapezu:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]]]]]]]

Gdzie s jest półprzewnikiem: s = (a+b+c+d)/2.

Inne relacje na wspinaczkę

Cięcie mediany z przekątnymi i równoległe przechodzące przez przecięcie przekątnych, powoduje inne relacje.

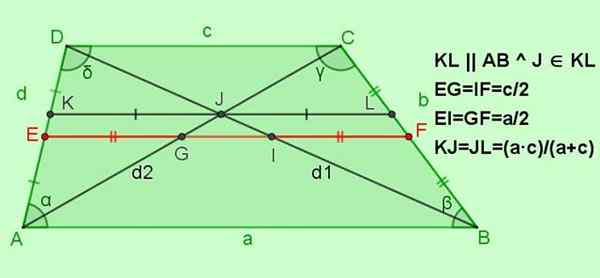Rysunek 5. Inne relacje na wspinaczkę. Źródło: f. Zapata.

-Relacje dla mediany EF

Ef = (a+c)/2; Np. = If = c/2; EI = gf = a/2

-Relacje dla segmentu równoległego do podstaw KL, a to przechodzi przez punkt Skrzyżowanie j przekątnych

Tak Kl || AB || DC z j ∈ Kl, a następnie kj = jl = (a ∙ c)/(a+c)

Konstrukcja trapez skalenicznego z regułą i kompasem

Biorąc pod uwagę podstawy długości Do I C, bycie> c i z boku długości B i D, istnienie B> d, Kontynuujemy wykonanie następujących kroków (patrz rysunek 6):

1.- Z regułą, segment największego AB jest narysowany.

2.- Z SE i na AB punkt P jest oznaczony tak, że AP = C.

3.- Z kompasem z C i Radio D Center rysowany jest łuk.

4.- Został wykonany w środku w B z Radio B rysując łuk, który interpretuje łuk narysowany w poprzednim kroku. Nazywamy to punktem przecięcia.

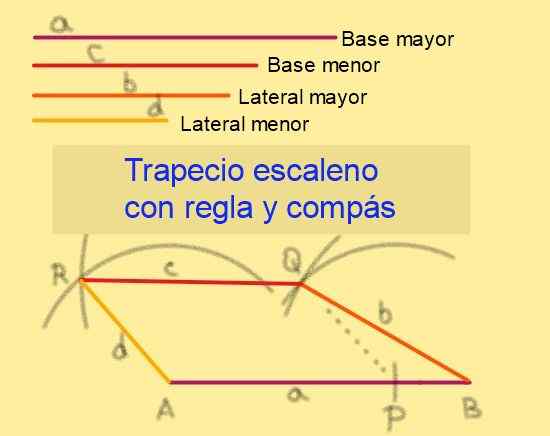Rysunek 6. Budowa Escaleno Trapecio według jego stron. Źródło: f. Zapata.

5.- Ze środkiem w rysowaniu promienia.

6.- Z centrum, w którym można rysować łuk promienia, który przechwycił się do łuku narysowanego w poprzednim kroku. Zostanie nazywany R do punktu cięcia.

7.- Segmenty BQ, QR i RA są rysowane z regułą.

8.- Abqr czworobok jest trapezem skaleniowym, ponieważ APQR jest równoległobokiem, który gwarantuje, że AB || Qr.

Przykład

Następujące długości podano w CM: 7, 3, 4 i 6.

a) Ustal, czy z nimi możesz zbudować trapez skalene, który może ograniczyć obwód.

b) Znajdź obwód, obszar, długość przekątnej i wysokość wspomnianego trapezu, a także promień zarejestrowanego obwodu.

- Rozwiązanie

Korzystając z segmentów o długości 7 i 3 jako zasad oraz o długości 4 i 6 jako boków, trapez skalenowy można zbudować przy użyciu procedury opisanej w poprzednim rozdziale.

Musimy sprawdzić, czy ma zarejestrowany obwód, ale pamiętanie właściwości (9):

Może ci służyć: heksagonalny pryzmat

Trapez ma zarejestrowany obwód tylko wtedy, gdy suma jego zasad jest równa suma jego boków.

Widzimy to rzeczywiście:

7 + 3 = 4 + 6 = 10

Wtedy spełniony jest stan wpisanego obwodu.

- Rozwiązanie b

Obwód

Obwód P jest uzyskiwany przez dodanie boków. Ponieważ podstawy łącznie 10, a także boki, obwód jest:

P = 20 cm

Obszar

Aby określić obszar, znany tylko jego boki stosuje się związek:

A = [(a+c)/| a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]]]]]]]]]

Gdzie S jest półprzewodnikiem:

S = (A+B+C+D)/2.

W naszym przypadku półprzewodnik jest wart s = 10 cm. Po wymianie odpowiednich wartości:

A = 7 cm; B = 6 cm; C = 3 cm; D = 4 cm

Zostaje:

A = [10/4] √ [(3) (7) (-1) (-3)] = (5/2) √63 = 19,84 cm².

Wysokość

Wysokość H jest związana z obszarem A poprzez następujące wyrażenie:

A = (a+c) ∙ h/2, gdzie wysokość można uzyskać przez klirens:

H = 2a / (a+c) = 2 * 19,84 / 10 = 3 968 cm.

Radio zarejestrowane obwód

Promień zarejestrowanego obwodu jest wart połowa wysokości:

R = h/2 = 1984 cm

Piagonals

Wreszcie jest długość przekątnej:

D₁ = √ [b² + A ∙ c - a (b² - D²)/(a - c)]

D₂ = √ [d² + A ∙ c - a (d² - B²)/(a - c)]

Prawidłowe zastępowanie wartości to:

D₁ = √ [6² + 7 ∙ 3–7 (6² - 4²)/(7 - 3)] = √ (36+21-7 (20)/4) = √ (22)

D₂ = √ [4² + 7 ∙ 3–7 (4² - 6²)/(7-3)] = √ (16+21-7 (-20)/4) = √ (72)

To znaczy: D₁ = 4,69 cm i d₂ = 8,49 cm

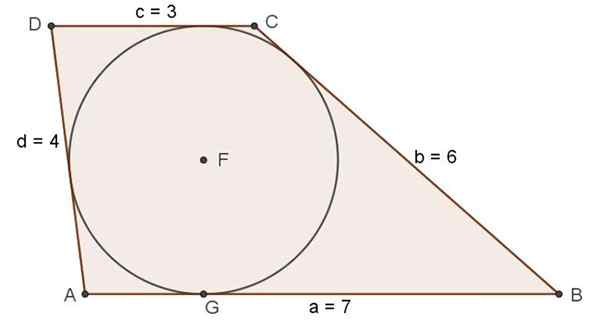Rysunek 7. Scalene trapezo, który spełnia stan istnienia zarejestrowanego obwodu. Źródło: f. Zapata.

Ćwiczenie rozwiązane

Określ kąt wnętrza trapezu podstawowego AB = A = 7, CD = C = 3 i boczny BC = B = 6, Da = D = 4.

Rozwiązanie

Twierdzenie cosinusowe można zastosować w celu ustalenia kątów. Na przykład kąt ∠A = α jest określany na podstawie trójkąta ABD z AB = A = 7, Bd = D2 = 8,49 i Da = D = 4.

Twierdzenie cosinusowe zastosowane do tego trójkąta pozostaje takie:

D₂² = a² + D² - 2 ∙ A ∙ D ∙ cos (α), to znaczy:

72 = 49+16-56 ∙ cos (α).

Podczas oczyszczania uzyskuje się cosinus kąta α:

Cos (α) = -1/8

To znaczy, że α = arccos (-1/8) = 97,18⁰.

W ten sam sposób uzyskane są inne kąty, będąc ich wartościami:

β = 41,41⁰; γ = 138,59⁰ i wreszcie δ = 82,82⁰.

Bibliografia

1. C. I. DO. (2003). Elementy geometrii: z ćwiczeniami i geometrią kompasu. University of Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematyka 2. Grupa redakcyjna Patria.
3. Freed, k. (2007). Odkryj wielokąty. Benchmark Education Company.
4. Hendrik, v. (2013). Uogólnione wielokąty. Birkhäuser.
5. Iger. (S.F.). Matematyka pierwszy semestr Tacaná. Iger.
6. Jr. Geometria. (2014). Wielokąty. Lulu Press, Inc.
7. Miller, Heeren i Hornsby. (2006). Matematyka: rozumowanie i aplikacje (wydanie dziesiąta). Edukacja Pearsona.
8. Patiño, m. (2006). Matematyka 5. Progreso redakcyjne.
9. Wikipedia. Trapez. Odzyskane z: jest.Wikipedia.com